Действительные числа
Понятие действительного числа
Действительные числа — это категории рациональных и иррациональных числовых значений.
Через R обычно выражается множество действительных чисел (их значения).
Рациональные числовые значения. Эту категорию чисел можно выразить, как положительное или отрицательное дробное значение. Еще есть вариант представлять рациональное число в виде нулевого значения.
Множество рациональных данных имеет следующий вид:
Иррациональное число. Данные значения невозможно выразить как деление двух и более целых данных. Такие числа представлены и выражаются как бесконечная, не имеющая определенного периода десятичная дробь.
Множество иррациональных чисел.
Данное множество, как правило, состоит из определенного множества рациональных чисел. А также, вместе с иррациональными значениями. Характеризуется множество R как область действительных чисел и обозначается
Иначе, можно составить и записать множество двух значений действительных чисел: рационального и иррационального.
Следовательно, любое рациональное число возможно записать в виде окончательной десятичной дроби или бесконечной периодической дроби. Иррациональные значения можно выразить бесконечными не имеющими определенного периода десятичными дробями. Учитывая все вышеизложенное определение действительных чисел можно составить и записать иначе.
Действительные числа — это значения чисел, которые выражаются, как конечная или бесконечная, имеющая вид периодической и непериодической десятичной дроби. Иными словами, их можно назвать, как вещественные.
Примеры действительных чисел
Действительные числа, могут быть и положительные, и отрицательные. Ноль, также будет являться действительным, потому что относится к категории рациональных значений, однако не будут иметь ни положительного ни отрицательного значения.

Используя действительные числа, можно выразить величины, числовые значения, которых изменяются непрерывно. Иначе говоря, действительные числа предоставляют возможность выражать числовые значение непрерывно, которые изменяя величины, через единичное значение.
Действительные числа на координатной прямой
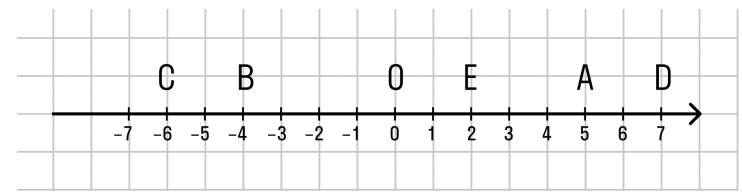
Координатная прямая — это прямая, на которой отображается заданная определенная точка отсчета. Начало берется за нулевое значение и единичный отрезок и заданное направление движения отсчета. Каждую точку прямой всегда выражают действительные значения чисел. Для каждой точки на координатной прямой соответствует действительное числовое значение, иными словами их называют координатные значения точек. Из этого следует, что между действительными и координатными значениями, всегда существует однозначная и определенная взаимосвязь и соответствие.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Класс и характеристика действительных чисел
Все действительные значения чисел можно представить по следующей классификации:
- простое натуральное значение или целое числовое значение — это простые числовые значения, которые возникают при простом и естественном счете. В технических науках множество целых числовых значений принято обозначать символом Z.
Любое значение множества натуральных чисел N — это, значение подмножеств целых числовых значений, которые обозначаются буквой Z .
Целым вполне возможно назвать, любое число натурального значения. Однако, целое число не всегда будет является натуральным числом, и это следует всегда помнить.
Натуральные числа, можно определить двумя методами:
значения, которые возникают, при подсчете определенных предметов, которые являются числительными (первый день, четвертый урок, третий ребенок);
обозначение конкретных событий или простых предметов (три слова, пять рулонов).
В первом случае нумерация начинается с единичного значения, а для второго характерен подсчет, с нулевого знака.
- положительное и отрицательное дробное значение, любого вида;
Простое положительное число — это как правило число, которое располагается с правой стороны от нулевого значения. Ему присвоен знак плюс, иными словами числа с плюсовым значением.
Например: 1;15;36;12356.
Рассмотрим значение 15 — целое число со знаком плюс, то есть положительное значение. На координатной прямой оно располагается справа от нулевого значения или точки первоначального отсчета.
Отрицательное число — это данное определение идентично вышеуказанному положительному, за исключение левой стороны от нулевого значения и знак меняется с плюса на минус.
Примеры целых отрицательных чисел: − 52 , − 258 , − 1 -528, -2568, -1. Нулевое значение делит между собой положительные и отрицательные целые числа. В тоже время оно, является ни положительным и ни отрицательным Числовое значение, которое является обратным каждому отрицательному значению, следовательно, является положительным целым числом.
Сравнивая с нулевым значением, можно сформулировать и другие определения, конкретно опираясь на ноль.
Например: числа, которые являются меньше нуля, можно назвать отрицательными целыми числовыми значениями.
Числа, которые больше нулевого данного числа, будет называться простыми положительными значениями. Положительные данные, находящиеся правее от нулевого числового значения, следовательно, отрицательные мы увидим слева от нуля. Мы уже рассмотрели и изучили правило, что натуральные числа — это целый ряд или подмножество целых значений. Рассмотрим это подробнее. Несколько данных натуральных чисел объединяют в себя целые положительные значения. Из этого следует, что множество отрицательных целых значений числа, может быть представлено, как множество значений, с обратным значением знака к натуральным числам. Стоит уделить внимание следующему понятию!
Любое натуральное число значение, может иметь свойство целого значения, однако, не каждое целое значение может быть натуральным. Отвечая на популярный вопрос, можно смело ответить — что являться не могут.
Дадим определения таким значениям неотрицательные и не положительные.
Неотрицательные целые числа — это положительные числа и нулевое числовое значение.
Неположительные целые числа — это отрицательные целые числа и значение равное нулю.
Как мы уже говорили ранее числовое данное равное нулю, не относится ни к какому из изученных натуральных значений. Простыми примерами неотрицательных чисел могут быть следующие значения: 45; 142; 26589;105689.
В свою очередь -52; -5698; -12598 это неположительные значения. Также есть смешанные значения, и дроби десятичного значения, они бывают:
- положительные;
- отрицательные;
- периодические;
- бесконечные;
- непериодические.
Выразить действительные числа, можно в следующем виде:
- корни числа;
- степенное значение;
- логарифмическое;
- сумма;
- разность;
- произведение;
- деление.
Применяя все перечисленные свойства числа действительного типа, можно составлять различного вида математические примеры, уравнения, тригонометрические и алгебраические функции. Составим и запишем несколько примеров решения:
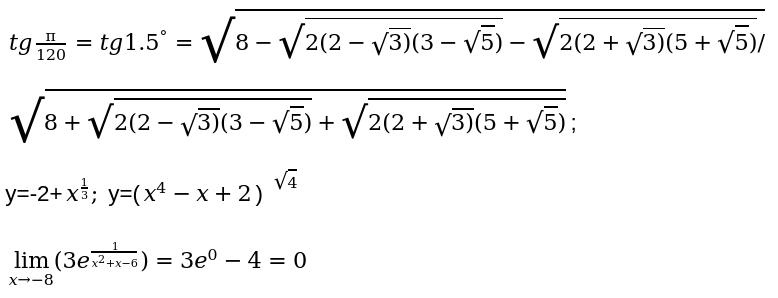
Принцип сравнения действительных чисел
Для множества R действительных чисел характерны формулы сокращенного умножения. Рассмотрим приме: a^2 — b^2 = (a — b)(a + b). Данное выражение справедливо на множестве только рациональных и действительных значений. Все действительные числовые значения сравнимы между собой. Для этого существую два основных способа.
Большим будет считаться, то значение которое располагается правее относительно координатной прямой.
√3 > √2; -3 > -5
Значение a будет больше числа b, при разности a — b > 0.
a > b <=> a — b > 0
Таким же способом определим, что a является меньше значением, чем b, когда разность a — b < 0
a < b <=> a — b < 0
Следовательно, будет справедливо равенство: a <= b <=> a — b <= 0.



