Электроемкость, конденсаторы
Если двум, находящимся на некотором расстоянии друг от друга, проводникам сообщить электрические заряды (q1 и q2), между ними появится электрическое поле. Разность потенциалов (Δφ) в нём будет определяться величинами сообщённых зарядов и формой, которую имеют проводники. Разность потенциалов между 2 точками постоянного во времени и однородного электрического поля называют напряжением (U).
Заряды, сообщённые проводникам, могут быть оба положительными, оба отрицательными или иметь разные знаки. Последний случай при равных абсолютных значениях зарядов нашёл в физике и электротехнике наибольшее применение и поэтому нам особенно интересен.
Электроемкость
Под конденсатором понимают систему из нескольких (чаще всего двух) находящихся близко друг от друга проводников, отделённых друг от друга слоем диэлектрика.
В подавляющем большинстве случаев его толщина много меньше размеров обкладок.
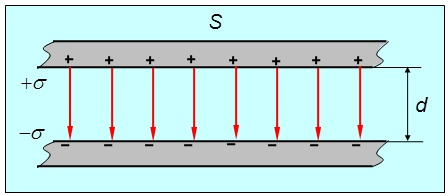
Электрической ёмкостью (C) между двумя проводниками называется скалярная величина, прямо пропорциональная абсолютной величине заряда одного из проводников и обратно пропорциональная разности потенциалов и напряжению между ними.
В виде формулы данное определение можно записать следующим образом:
\[C=(q / \Delta \varphi)=(q / U)\]
В системе СИ электроёмкость измеряют в Фарадах. Один Фарад равен электроемкости конденсатора, при которой заряд, равный 1 Кулону, создаёт между его пластинами напряжение в 1 Вольт.
\[1 \Phi=\frac{1 \mathrm{~Kл}}{1 \mathrm{~B}}\]
Ёмкость в 1 Фарад – величина очень большая. На практике чаще всего используют мили фарады (одна тысячная фарада), микрофарады (одна миллионная), нанофарады (одна миллиардная), пикофарады (10 в минус 12-й степени).
Плоским называют конденсатор, образованный двумя плоскими, параллельно расположенными по отношению друг к другу пластинами. Если роль диэлектрика между ними играет воздух, то такой конденсатор называют воздушным.
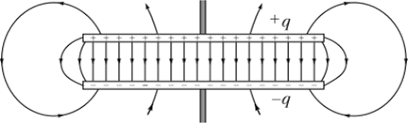
Электрическое поле в плоском конденсаторе сосредотачивается главным образом между пластинами, однако часть его выходит за их пределы. Это вышедшее поле называют полем рассеяния. Оно не является потенциальным, т.е. работа при перемещении в нём заряда из одного места в другое не равна нулю.
Обычно такое поле не велико и при решении многих (но далеко не всех) задач его наличием можно пренебречь.
Абсолютную величину напряжённости каждой из обкладок можно выразить формулой:
\[E_{1}=\frac{\sigma}{2 \varepsilon_{0}}\].
Где σ это плотность электрического заряда на плоскости. По принципу суперпозиции полная величина напряжённости поля конденсатора равна сумме напряжённостей полей от каждой из его обкладок.
\[\vec{E}=\overrightarrow{E^{+}}+\overrightarrow{E^{-}}\]
Т. к. между пластинами векторы \[\overrightarrow{E^{+}} \text {и } \overrightarrow{E^{-}}\] параллельны, полную напряжённость можно вычислить по формуле \[E=2 E_{1}=\frac{\sigma}{\varepsilon_{0}}\].
Вне пластин поля каждой из них компенсируют друг друга, и потому общая их напряжённость равна нулю.
Как вычислить электроемкость плоского конденсатора
Вспомним, как ёмкость зависит от заряда пластин и разности потенциалов между ними. Это формула \[\mathrm{C}=(\mathrm{q} / \Delta \varphi) . \text { Заряд } \mathrm{q}=\sigma * \mathrm{~S}, \mathrm{~S}\] – площадь одной обкладки.
Разность потенциалов в однородном электростатическом поле равна напряжению и вычисляется по формуле \[\Delta \varphi=\mathrm{E}^{*} \mathrm{~d}\]
Подставляем эти значения в формулу для ёмкости. В результате получаем:
Т. к. электрическая постоянная ε0 равна σ/E в итоге получаем \[C=\frac{q}{\Delta \varphi}=\frac{\sigma \cdot S}{E \cdot d}=\frac{\varepsilon_{0} S}{d}\].
Теперь давайте определим электроемкость конденсатора в форме сферы и цилиндра.
Сферический конденсатор
Им называют систему двух проводящих, расположенных одна в другой сфер с радиусами R1 и R2. Будем исходить из того, что они имеют общий центр.
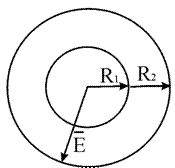
\[\varphi_{1}-\varphi_{2}=\int E d x=\int \frac{k Q d r}{r^{2}}=k Q\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\] т. к. \[C_{c \Phi}=\frac{Q}{k Q\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)}=\frac{4 \pi \varepsilon \varepsilon_{0} R_{1} R_{2}}{R_{2}-R_{1}}\]
У нас R2 -R1 << R1. Это значит, что R1 и R2 можно принять равными R, тогда произведение радиусов в формуле можно будет считать квадратом R.
R2 – R1=d
Исходя из того что \[C_{c \Phi}=\frac{4 \pi \varepsilon \varepsilon_{0} R^{2}}{d}\] и \[S_{c \Phi}=4 \pi R^{2}\].
В итоге получаем \[C=\frac{\varepsilon \varepsilon_{0} S}{d}=\frac{4 \pi \varepsilon \varepsilon_{0} R^{2}}{R_{2}-R_{1}}\].
Цилиндрический конденсатор
Им называют систему находящихся один в другом цилиндров.
Для упрощения расчётов расположим их на одной оси.
Если пренебречь краевыми эффектами, то \[\varphi_{1}-\varphi_{2}=\frac{\lambda}{2 \pi \varepsilon \varepsilon_{0}} \ln \left(\frac{r_{2}}{r_{1}}\right)=\frac{q}{2 \pi \varepsilon \varepsilon_{0} l} \ln \left(\frac{r_{2}}{r_{1}}\right)\]
\[C=\frac{q}{\varphi_{1}-\varphi_{2}}=\frac{2 \pi \varepsilon_{0}}{\ln \left(\frac{r_{2}}{r_{1}}\right)}\].
Теперь вы знаете, чему равна электроемкость конденсатора, давайте рассмотрим их соединения в электрической цепи.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Расчёт электроемкости батареи конденсаторов
Батареей статических конденсаторов называют группу конденсаторов, связанных между собой электрическим соединением.
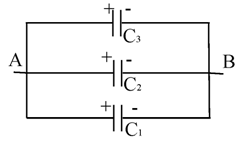
У параллельно соединённых конденсаторов одинакова разность потенциалов между обкладками Q1= С1 (φА- φВ), Q2= С2 (φА- φВ), Q3 = С3 (φА- φВ). Заряд батареи складывается из зарядов каждого из отдельных конденсаторов, в неё входящих. Поэтому легко понять почему
\[Q=\sum_{i-1}^{N} Q_{i}=\sum_{i=1}^{N} C_{i}\left(\varphi_{\mathrm{A}^{-}} \varphi_{\mathrm{B}}\right)\]
Суммарная ёмкость батареи при таком раскладе равна
\[C_{\text {парал }}=\frac{Q}{\varphi_{A}-\varphi_{B}}=\sum_{i=1}^{N} C_{i}\]
Выходит, что при параллельном соединении ёмкости просто складываются.
При последовательном соединении конденсаторов ситуация будет совершенно другой.
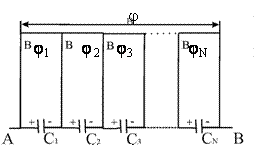
В этом случае заряды обкладок всех входящих в батарею конденсаторов равны по абсолютной величине. Разность потенциалов на её концах равняется сумме разностей потенциалов на каждом из них. В виде формулы можно записать таким образом Dj=Dj1 + Dj2 + ….+ Dj.
Для каждого из конденсаторов батареи справедливы соотношения:
\[\frac{1}{C_{\text {посл }}}=Q \sum_{i=1}^{N} C_{i}\].
Из этого следует однозначный вывод, что при последовательном соединении ёмкость батареи всегда меньше ёмкости любого из её конденсаторов.
Электроемкость конденсатора колебательного контура
Колебательным контуром называют электрическую цепь, содержащую конденсатор, катушку индуктивности и источник электричества.
Мы для вычисления ёмкости будем рассматривать упрощённую его схему, состоящую только из конденсатора и катушки. Сопротивление соединяющих их проводников положим равным нулю. Сопротивлением катушки и излучением электромагнитных волн тоже пренебрегаем. Такой контур называют идеальным.
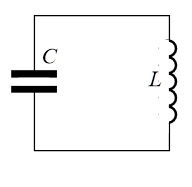
Придадим обкладкам конденсатора заряды –Q и +Q. В начальный момент времени электроемкость конденсатора контура будет \[W_{C}=\frac{Q^{2}}{2 C}\].
Это максимальное значение ёмкости конденсатора в контуре. Выше него никак не будет.
Если замкнуть конденсатор на катушку, он начнёт разряжаться, возникнет электрический ток. В катушке появится и станет возрастать магнитное поле. В максимуме, когда конденсатор полностью разрядится, энергия порождённого током поля будет \[W_{L}=\frac{1}{2} L I^{2}\].
Полная энергия системы останется постоянной и равна \[W_{\text {полн}}=\frac{1}{2}\left(\frac{Q^{2}}{C}+L I^{2}\right)=\mathrm{const}\].
Электроемкость конденсатора, энергия которого известна, из приведённых формул вычисляется достаточно легко:
C=Q2/(2W-LI2)
В контуре станут происходить гармонические колебания, общее их уравнение \[\ddot{Q}+\frac{1}{L C} Q=0\].
Его решение: \[Q(t)=Q_{m} \cos \omega_{0} t\]
Для силы тока и напряжения получим
\[I=\frac{d Q}{d t}=-\omega_{0} Q_{m} \sin \omega_{0} t=I_{m} \cos \left(\omega_{0} t+\frac{\pi}{2}\right)\], \[U_{C}=\frac{Q}{C}=\frac{Q_{m}}{C} \cos \omega_{0} t=U_{m} \cos \omega_{0} t\].
Чтобы получить формулу электроемкости конденсатора колебательного контура в любой момент времени, следует обе части
\[U_{C}=\frac{Q}{C}=\frac{Q_{m}}{C} \cos \omega_{0} t\]
Умножить на C и поделить на Uc.
В результате получим: \[C=\frac{Q_{m}}{U_{C}} \cos \omega_{0} t\].














