Изотермический процесс

4 373

31 октября 2022 г.

Время чтения: 4 минуты

Содержание:

Изотермический процесс для температуры газа, основные формулы и величины
Изотермический процесс для системы координат
Изотермический процесс - закон Бойля-Мариотта
Как найти изотермический процесс - примеры решения задач

Для изотермического процесса характерен определенный процесс, который происходит с газовым веществом, который в свою очередь имеет неизменную массу и постоянную неизменяемую температуру вещества.

Изотермический процесс для температуры газа, основные формулы и величины

Формулы

Изотермический процесс характеризует состояние газа и данное состояние записывается следующими формулами:

\[p_{1} V_{1}=v R T\]

\[p_{2} V_{2}=v R T\]

Изотермический процесс для системы координат

Характерные изотермические процессы зачастую отражают на термодинамических графиках и диаграммах.

Если рассмотреть подробно график можно увидеть линию, именно ее и принято называть изотермой. Она непосредственно является основной характеристикой процесса.

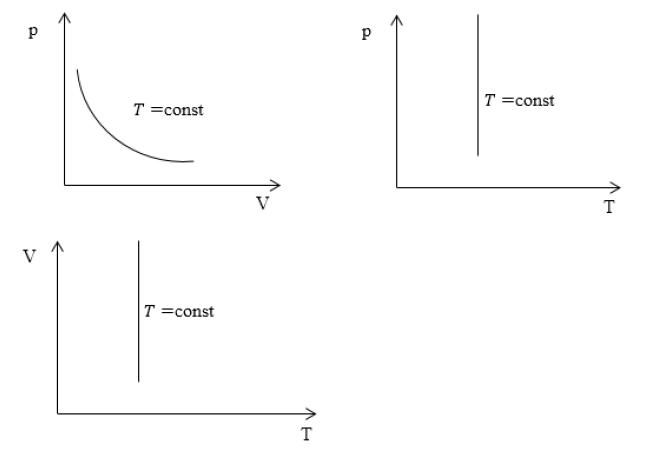
Изотермический процесс для системы координат

Изотермический процесс — закон Бойля-Мариотта

Разделим уравнение для второго состояния газа на выражение первого состояния и получим основное уравнение изотермического процесса.

\[\frac{p_{2} V_{2}}{p_{1} V_{1}}=1\] или \[p V=\mathrm{const}\] (постоянное значение)

Полученное уравнение и будет называться законом Бойля-Мариотта.

Данный процесс осуществляется с использованием тепловой энергии.

В случае, когда объем увеличивается, или отводится, для его уменьшения.

Составим первое значение термодинамики.

Затем постепенно получим уравнение для определения работы.

А также вычисления внутренней энергии и количества теплоты тела при изотермическом процессе.

\[\delta Q=d \cup+d A=\frac{i}{2} v R d T+p d V\]

Температура является неизменной, поэтому, изменение значения внутренней энергии будет равняться нулевому значению. \[(d \cup=0)\].

Из этого следует, что для изотермического процесса все подводимое тепло направлено на работу, которую совершает газ:

\[ \Delta Q=\int_{V_{1}}^{V_{2}} d A \]

где:

\[\delta Q\] — тепло элементарного характера, которое подводится ко всей системе;
dA — работа элементарного типа, совершаемая газом в изотермическом процессе;
i — количество свободных степеней газовых молекул;
R — газовое значение постоянной;
d — значение молей для газа;
V₁— первоначальное значение объема газа;
V₂— окончательное значение объема газа.

\[A=\int_{V_{1}}^{V_{2}} p d V\]

Давление газа, которое зависит от уравнения газа в идеальном состоянии.

\[p V=v R T \rightarrow p=\frac{v R T}{V}\]

Подставим вышеуказанное выражение в подынтегральное выражение:

\[A=\int_{V_{1}}^{V_{2}} \frac{v R T}{V}=v R T \int_{V_{1}}^{V_{2}} \frac{d V}{V}=\mathrm{u} R T \ln \left(\frac{V_{2}}{V_{1}}\right)\]

Составленное уравнение необходимо определения значения работы, которую совершает газ в изотермическом процессе.

\[ A=v R T \ln \left(\frac{p_{1}}{p_{2}}\right) \]

\[ \Delta Q=A \]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как найти изотермический процесс — примеры решения задач

Пример №1

Основное содержание задания: газ идеального состояния, имеет способность расширяется, имея постоянную температуру, от объема.

\[V_{1}=0.2 \mathrm{~m}^{3}\]

\[V_{2}=0.6 \mathrm{~m}^{3}\]

Известно сила давления во втором состоянии и оно равняется \[p_{2}=1 \cdot 10^{5} \mathrm{\Pi a}\].

Определить:

Величину изменения внутренней энергии газа;
Значение работы, которую совершает газовое вещество в данном процессе;
Какое необходимое количество теплоты получает газ в процессе работы.

Методика решения:

Внутренняя энергия газа неизменна, так как процесс который рассматривается в задаче, является изотермическим:

\[\Delta \mathrm{U}=0\]

Из основного закона термодинамики можно определить:

\[\Delta \cup=A\]

\[A=v R T \ln \left(\frac{V_{2}}{V_{1}}\right)\]

Составим и запишем уравнение, которое отражает окончательное (конечное) состояние газа:

\[p_{2} V_{2}=v R T \rightarrow T=\frac{p_{2} V_{2}}{v R}\]

Подставим в уравнение для температуры вышеизложенные формулы и получим решение:

\[A=v R \frac{p_{2} V_{2}}{v R} \ln \left(\frac{V_{2}}{V_{1}}\right)=p_{2} V_{2} \ln \left(\frac{V_{2}}{V_{1}}\right) .\]

Следовательно, все величины расположены в международной системе единиц (СИ), можно провести вычисления и определить неизвестные значения:

\[A=0.6 \cdot 10^{5} \ln \left(\frac{0.6}{0.2}\right)=0.6 \cdot 10^{5} \cdot 1.1=6.6 \cdot 10^{4} \text { (Дж) }\]

Ответ задачи:

значение изменения внутренней энергии газа в рассматриваемой процессе равно нулевому значению.
работа, которая совершается в процессе газовым веществом равняется \[6,6 \cdot 10^{4} \text { Дж }\].
Необходимое количество тепловой энергии равно: \[6,6 \cdot 10^{4} \text { Дж }\].

Пример №2

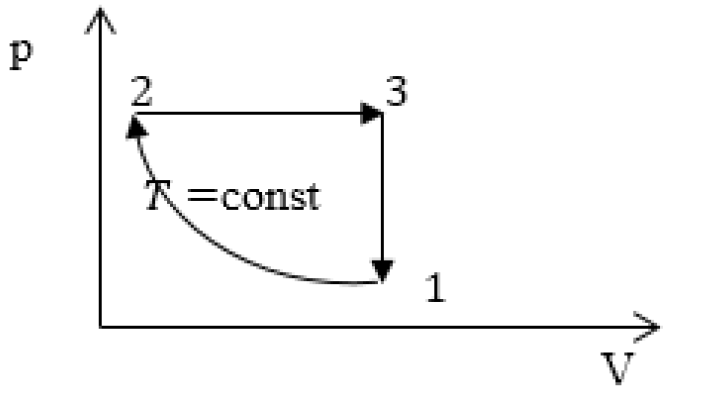
Задание: изображен график, где изменяется идеальное состояние массы газа равное m в координатных осях p (V).

Нужно перенесите данный процесс на координатные оси в p(T).

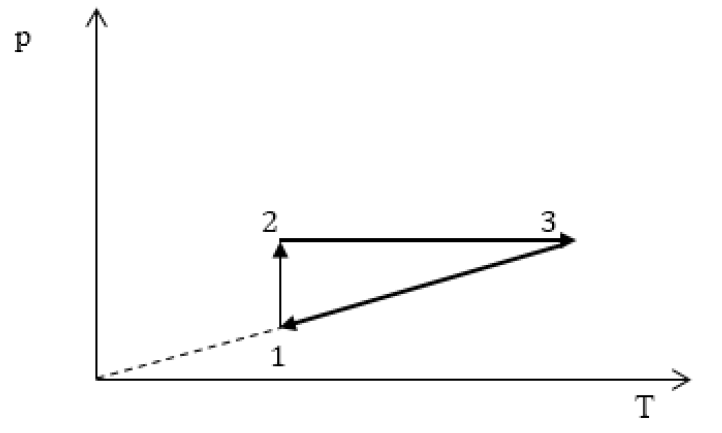
На данном графике изображен круговой процесс.

Где:

Прямая 1-2 является изотермическим процессом с константой \[(T=\text { cons } t)\]. Следовательно значение объема будет уменьшается \[(\mathrm{V} \downarrow)\], а давления соответственно расти \[(p \uparrow)\].
Прямая 2-3 отражает изобарический процесс \[(p=\text { const })\]

const). Для данного процесса характерно увеличение объема \[\mathrm{V} \uparrow\] и применяя закон Гей-Люссака, увеличение \[Т \uparrow\]

Прямая (отрезок) 3-1 является изохорным процессом объем будет постоянной величиной \[(\mathrm{V}=\text { const })\], а \[p \downarrow\],а исходя из закона Шарля \[T \downarrow\].

Все перечисленные процессы изобразим на координатных осях p(T).