Равноускоренное движение
Равноускоренным движением называется движение при котором скорость за одинаковое время изменяется на одно и то же значение. В физике это самый простой вид движения с ускорением.
К примерам движения тела с постоянным ускорением можно отнести падение камня с обрыва, полёт гранаты, после выстрела из гранатомёта, скатывание санок с горы. Равномерное движение можно считать частным случаем равноускоренного, при котором ускорение всегда остаётся равным нулю.
Давайте подробно рассмотрим движение тела под действием постоянного поля силы тяжести вблизи земли. Пусть оно будет брошено под углом к горизонту. Это одновременно и равномерное и равноускоренное движение. Равномерное – по горизонтали (оси X), равноускоренное – по вертикали (оси Y). Сопротивлением воздуха, влиянием на движение вращения Земли и другими подобными факторами пренебрегаем.
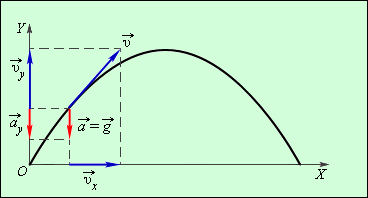
В каждой точке пути на тело действует постоянное ускорение g. Оно не меняется ни по величине, ни по направлению.
Основные формулы равноускоренного движения и график равноускоренного движения
Скорость при равноускоренном движении тела вычисляется с помощью выражения:
\[v=v0+at\];
\[v0 – \text { начальная скорость тела; }\]
\[a=const – \text { —ускорение; }\]
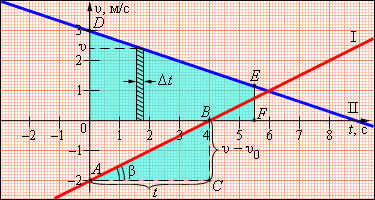
Ускорение здесь определяется, как угол наклона графика скорости. Посмотрите на треугольник ABC.
a=(v-v0)/t=BC/AC.
Чем больше угол β, тем более наклонно выглядит график ускорения по отношению к оси времени. Следовательно, тем большее значение имеет ускорение тела.
Для первого из графиков положим V0=-2м/с. a=0,5м/с².
Для второго графика положим V0=3м/с. a=(-1/3)м/с².
Указанный график позволяет понять многие зависимости равноускоренного движения и вычислить его основные параметры при проецировании на направление движения. Сначала нужно выделить на графике крохотный отрезок времени Δt. Будем считать его настолько коротким, что движение на нём можно принять за равномерное со значением скорости равным скорости в середине указанного временного промежутка. Тогда, перемещение Δs за Δt можно принять равным Δs=vΔt. Заштрихованная область на первом из графиков.
Разделим всё время движения тела на такие бесконечно короткие промежутки Δt. Перемещение s за указанное время t будет равняться площади трапеции обозначаемой ODEF.
S=(|OD|+|EF|/2)*OF|= [(v+v0)/2]*t =[2v0+(v-v0)]*t/2;
Как известно, v-v0=at, исходя из этого окончательная формула равноускоренного движения выглядит следующим образом:
S=v0*t+at²/2
Чтобы узнать, какой будет координата тела в любое время его движения, к начальной координате следует ещё вписать перемещение. Изменение координаты в зависимости от времени есть закон равноускоренного движения по оси Y:
Y=y0+v0*t+at²/2.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Закон равноускоренного движения
\[Y=y0+v0*t+at²/2\];
Из него видна зависимость равноускоренного движения от начального положения и начальной скорости тела. Если то и другое равно нулю, график равноускоренного движения приобретает вид параболы, пересекающей начало координат и обращённой своими ветвями вниз. Само движение при этом будет происходить по прямой вертикальной линии. Выражение станет законом равноускоренного прямолинейного движения.
S=at²/2
Это самый простой класс равноускоренного движения. Вектор скорости тела в нём всегда направлен по оси Y, меняет только свой знак. С формулами равноускоренного прямолинейного движения работать легче всего, поэтому при решении задач нужно стараться выбрать систему отсчёта именно таким образом.
Подставляя разные начальные значения скорости и координаты, меняя знак ускорения, можно получить самые разные значения. Вы спросите –«Зачем менять знак ускорения? Оно ведь всегда постоянно и направлено точно вниз.» При решении задач, чтобы найти равноускоренное движение, часто бывает удобно изменить направление оси Y, вместе с этим меняется и знак ускорения, оно становится положительным.
Как найти равноускоренное движение тела, если неизвестно время
Часто возникает задача нахождения координаты тела при заданной начальной скорости движения тела, конечной скорости его движения и ускорении, но не заданном времени. Как быть в этой ситуации.
Рассмотрим уравнения:
v=v0+at;
S=v0*t+at²/2
Как систему уравнений. Для её решения, нужно исключить переменную t.
Сначала находим t из первого уравнения
t=(v-v0)/a
Затем подставляем его в выражение для перемещения. В результате получаем уравнение равноускоренного движения, не содержащее время.
s=[v²- (v0)²]/2a
Из данного выражения уже достаточно легко вычислить скорость. Она равна:
V=√(v0)²-2as
При v0=0 s=v²/2a и v=√2as














