Угловое ускорение
Нам уже известно понятие ускорения тела. Так именуют величину, характеризующую изменение его скорости. Также нам известно понятие угловой скорости. Для характеристики этого изменения используют величину, называемую угловым ускорением. Рассмотрим его особенности и использование.
Определения углового ускорения тела. Среднее и мгновенное угловое ускорение
Угловым ускорением называется кинематическая величина, характеризующая изменение угловой скорости с течением времени. Обозначают его обычно греческой буквой ε.
Слово «кинематическая» означает, что движение рассматривается без учёта действия на тело сил, независимо от них. Обозначим промежуток времени как Δt. Изменение угловой скорости за этот промежуток обозначим как Δω. Отношение Δω/Δt называют средним угловым ускорением. Среднее угловое ускорение равно угловой скорости за определённый интервал времени. Однако, как она себя вела, например, в самом его начале, середине или конце ничего не скажешь.
Если мы будем выбранный нами интервал времени постоянно уменьшать, изменение скорости получится описывать всё более и более точно. В идеале, чтобы Δt вообще стремился к нулю:
ε = lim (Δt→0)(Δω/Δt) = dω/dt = d2φ /d2t
Так мы перешли ко второму определению углового ускорения, только оно уже не среднее, а, как говорят, мгновенное.
Угловое ускорение тела есть первая производная его угловой скорости по времени или вторая производная его углового перемещения. Ещё раз перепишем формулы, но уже в качестве официального определения.
Угловое ускорение тела равно:
ε = dω/dt = d2φ /d2t
Размерностью величины будет 1/T2 (1/время2). Измеряют его обычно в радианах на секунду в квадрате, рад/с2 или 1/с2 (с-2).
Обязательно следует отметить, что ε может рассматриваться, в качестве вектора, т. е. ему приписывается направление. Хотя в отличие от направления обычной скорости, воспринимается это несколько сложнее, ведь наглядность отсутствует.
Угловое ускорение через радиус выражается как a = ε*R, где a – ускорение, направленное по касательной траектории.
Если тело вращается всё быстрее и быстрее, то это значит, что модуль его угловой скорости с течением времени увеличивается. Такое вращение называют ускоренным. При нём вектора угловых скорости и ускорения имеют одно и то же направление.
Если тело вращается всё медленнее и медленнее, то это значит, что модуль его угловой скорости со временем уменьшается. Такое вращение называют замедленным. При нём вектора угловой скорости и углового ускорения направлены противоположно.
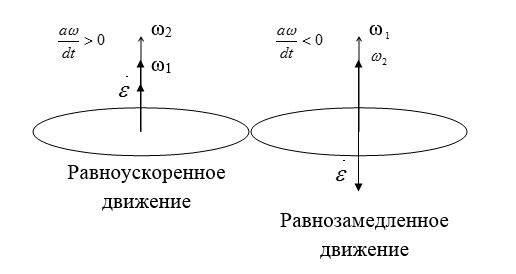
Угловое ускорение и формула закона движения при равнопеременном вращении
Равнопеременным вращением называют вращение, при котором угловое ускорение не меняется с течением времени, т. е. является константой \[(ε=const)\].
Выведем его закон. Пусть в начальный момент времени (t=0) равен φ0, а его начальная скорость ω0.
Из определений выше следует
ε = dω/dt следует, что dω = ε dt.
Чтобы найти угловую скорость нам нужно найти первообразную от этого выражения по времени. Получаем
ω = εt + С1.
С1 – некоторая постоянная. В нашем случае, по начальным условиям, она равна начальной угловой скорости тела, ω0.
Поэтому
ω = εt + ω0
Напомним, что мгновенная угловая скорость равна: ω = dφ /dt
Отсюда
dφ /dt = εt + ω0
φ = (εt + ω0)dt
Находим первообразную по времени
φ = εt2/2 + ω0t + С2
С2 – некоторая постоянная. Исходя из начальных условий она равна φ0. Приходим к выражению
φ = εt2/2 + ω0t + φ0
Это и есть закон равнопеременного вращательного движения.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры
Пример. 1
Колесо стало вращаться с постоянным угловым ускорением и, спустя 10 оборотов от начала вращения, получило скорость 20 рад/с. Чему равно угловое ускорение?
Решение:
Применим к вращению колеса формулу равнопеременного движения, исходя из того, что его начальная угловая скорость ω0 была равна нулю. Формулы, с которыми нам придётся иметь дело:
φ = εt2/2; ω = εt; φ = 2πN
Из первой формулы выражаем ε
ε = (φ/t2)
Из второй формулы выражаем время
t = ω/ε
Подставляем его в формулу выше.
ε = (2*φ)/(ω/ε)2 = ( 2* φ * ε2)/ω2
Проводим необходимые сокращения и приходим к формуле углового ускорения:
ε = ω2/2φ
Вместо угла φ подставляем в выражение третью формулу
ε = ω2/2*2πN = ω2/4πN
После подстановки численных значений получим ε = 3,2 рад/c2
Ответ: Угловое ускорение колеса равно 3,2 рад/c2.
Пример. 2
Тело вокруг собственной оси вращается по следующему закону:
φ = 10 + 20*t – 2*t2
Нужно найти угловое и полное ускорение точки, находящейся в 109 см. от оси вращения через 4 секунды после начала движения.
Решение:
Формулы, с которыми нам придётся иметь дело:
\[a=\sqrt{a_{n}^{2}+a_{T}^{2}}\]
At = dv/dt = Rε
an = v2/R = ω2R
Если известен закон движения, то ω и ε не составляет труда выразить через производные. Сначала находим ω.
ω = d(10 + 20t – 2t2)/dt = 20 – 4t
Ускорение находим, дифференцируя последнее полученное выражение:
ε = d(20 — 4t)/dt = (- 4 )рад/с2
Смотрим на формулу нахождения полного a и выражение ε через радиус, после чего делаем соответствующие подстановки.
\[a=\sqrt{R^{2} \varepsilon^{2}+\omega^{4} R^{2}}\]
После численных подстановок выясняем, что a точки равно 1,65 м/с2.
Ответ: Угловое ускорение точки равно (-4) рад/с2, а полное её ускорение – 1,65 м/с2.














