Самоиндукция. Энергия магнитного поля
Самоиндукция — это один из случаев электромагнитной индукции, при котором электромагнитный поток создается при протекании через контур тока, при этом он изменяется и вызывает ЭДС индукции.
Понятие об ЭДС самоиндукции
При явлении самоиндукции, если ток конкретного контура изменен, то меняется магнитное поле данного тока, а значит и всего магнитного потока, который проходит через конкретный контур. При этом в контуре создается ЭДС самоиндукции, которая создает препятствие на пути изменения электрического тока в контуре. Если цепь, которая имеет постоянный источник тока, замыкают, то сила тока появляется не мгновенно, при размыкании цепи электрический ток не пропадает сразу, а через некоторое время самоиндукция исчезает.
Формула самоиндукции
Магнитный поток Φ, проходящий через катушку с током или контур постоянных форм и размеров, является пропорциональным силе тока I.
Самоиндукция определяется по формуле:
\[\boldsymbol{\Phi}=\boldsymbol{L} \boldsymbol{I}\]
Коэффициент пропорциональности L в формуле Ф = L I, это и будет коэффициент самоиндукции. Она тесно связана с формой, размерами контура, магнитными показателями и свойствами вещества, в котором расположен контур.
Закон, которому подчиняется ЭДС самоиндукции:
\[\varepsilon=-L \frac{d I}{d t}\]
Если контур имеет постоянные размеры и форму, то ЭДС самоиндукции энергии магнитного поля прямо пропорциональна скорости изменения силы тока в конкретном контуре.
Единица индуктивности в СИ имеет общепринятое название Генри, обозначается — Гн.
Индуктивность катушки или контура равна 1 Гн, в случае силы тока в 1 А, поток составляет 1 Вб:
\[1 \Gamma н=\frac{1 B б}{1 A}\]
Сила самоиндукции зависит от скорости увеличения/уменьшения магнитного поля. При этом может меняться магнитное поле, а также контур может менять положение в магнитном поле.
Как рассчитать индуктивность
Для расчета индуктивности рассмотрим длинный соленоид — это цилиндрическая катушка индуктивности, длина которой значительно больше диаметра.
Соленоид из примера имеет N витков, длину L, площадь сечения S.
\[B=\mu_{0} \boldsymbol{n} \boldsymbol{I}\]
где I — это обозначение тока в соленоиде, \[n=\frac{N}{e}\]
n показывает количество витков соленоида на единицу его длины.
Магнитный поток, проходящий через все N витков внутри катушки соленоида, составляет:
\[\Phi=B \cdot S \cdot N=\frac{\mu 0 n^{2} S}{L}\]
Индуктивность соленоида будет выражена формулой:
\[L=\mu 0 n^{2} S \cdot l=\mu 0 n^{2} V\]
где V = S·l , это объем длинного соленоида.
Рассмотренный пример является приближенно верным для катушек достаточной длины, так как не берется в расчет краевой эффект. В случае, если соленоид заполнен веществом, которое имеет магнитную проницаемость μ, при действии заданного тока I, индукция магнитного поля будет возрастать по модулю в μ раз. Следовательно, индуктивность катушки с сердечником тоже будет увеличиваться в μ раз:
\[L_{\mu}=\mu \cdot L=\mu 0 \cdot \mu \cdot=n^{2} \cdot V \]
ЭДС самоиндукции в цепи
В соответствии с законом Фарадея, ЭДС самоиндукции записывается по формуле:
\[\delta_{инд}=\delta_{L}=\frac{-\Delta \Phi}{\Delta t}=-L \frac{\Delta I}{\Delta t}\]
ЭДС самоиндукции равна значению, которое прямо пропорционально индуктивности катушки и скорости изменения силы тока, проходящего через нее.
Носителем энергии будет магнитное поле. Катушка, по виткам которой проходит ток, обладает запасом энергии, по аналогии с заряженным конденсатором.
Если параллельно катушке с большим показателем индуктивности включить в цепь постоянного тока электрическую лампу, то при размыкании цепи ЭДС самоиндукции цепи вызовет ток, будет наблюдаться которая вспышка лампы.
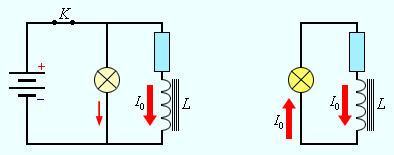
На рисунке изображена цепь, в момент размыкания ключа К, происходим короткая вспышка электрической лампы. Ток в цепи возникает под воздействием ЭДС самоиндукции, а источником энергии, которая будет выделяться в цепью, будет магнитное поле катушки.
Исходя из закона сохранения энергии, можно сделать вывод, что вся энергия, выделенная из катушки, будет отдана в виде джоулева тепла.
Если R – полное сопротивление цепи, тогда за интервал времени Δt будет выделено теплоты:
\[\Delta Q=I^{2} \cdot R \cdot \Delta t\]
Ток в цепи можно выразить формулой:
\[I=\frac{\delta_{L}}{R}=\frac{-L}{R} \frac{\Delta I}{\Delta t}\]
Формула исчисления выделенной теплоты Δt можно записать таким образом:
\[\Delta Q=-L \cdot I \cdot \Delta I=-\boldsymbol{\Phi}(I) \Delta I\]
где \[\Delta I<0\], а значение тока в цепи постепенно понижается до нуля от изначального \[I_{0}\].
Вся теплота, которая выделится в цепи, можно получить при интегрировании в пределах от \[I_{0}\] до нуля. И получаем:
\[Q=\frac{L I_{0}^{2}}{2}\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Графические выводы по теме
Запишем полученную формулу используя графический метод. Для этого изобразим на графике самоиндукции взаимосвязь магнитного потока Φ(I) от тока I.
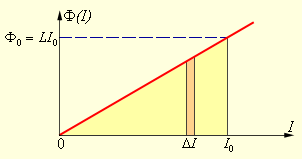
Полное количество выделившейся теплоты, которое соответствует запасу энергии магнитного поля, равно площади треугольника на рисунке 2.
Получаем, что формула энергии \[W_{M}\] магнитного поля катушки, индуктивность которой равна L, создаваемого током I, можно записать в виде формулы:
\[W_{M}=\frac{\Phi I}{2}=\frac{L I^{2}}{2}=\frac{\Phi^{2}}{2 L}\]
Применив выражение, которое получили для энергии катушки с сердечником длинного соленоида. Используя формулы для коэффициента самоиндукции \[L_{\mu}\] соленоида и для магнитного поля В, под действием тока I, можно выразить следующим образом:
\[W_{M}=\frac{\mu_{0} \cdot \mu \cdot n^{2} \cdot I^{2}}{2} V=\frac{B^{2}}{2 \mu_{0} \cdot \mu} V\]
где V — объем соленоида.
Данная формула показывает, что магнитная энергия располагается не в витках катушки, по которым идет электрический ток, а распределена по всему объему катушки, охваченном магнитным полем.
Объемная плотность магнитной энергии — это физическая величина, которая равняется энергии магнитного поля на единицу объема, выражается формулой:
\[W_{\mu}=\frac{B^{2}}{2 \mu_{0} \cdot \mu} V\]
Максвелл продемонстрировал, что данная формула подходит для любых магнитных полей.
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике