Деформация и ее виды
Аморфные и кристаллические тела состоят из частиц, постоянно находящихся в состоянии теплового колебания. Небольшое отклонение от положения равновесия обусловлено минимальной энергией их взаимодействия. В зависимости от дальности пребывания частиц, между ними действуют две силы: чем меньше расстояние, тем больше сила отталкивания, а притяжение увеличивается вместе с отдалением частиц друг от друга. Данные силы определяют свойства механического характера всех твёрдых тел, а изменение внутреннего положения их частиц под воздействием силы притяжения и отталкивания называется деформацией.
Виды деформации
Воздействие на тело других тел способно изменять как его форму, так и размеры, происходит это в результате приложенной силы, которая может носить разный характер. Являясь физической величиной, сила имеет не только значение (модуль), но и направление – вектор, от которого зависит, каким видом деформации обернётся воздействие. Приложенное напряжение перпендикулярно к телу или по касательной может придавать пять видов деформации.
Изменение тела может быть представлено:
- сжатием;
- растяжением;
- сдвигом;
- кручением;
- изгибом.
Деформация сжатия вызывается напряжением, направленным к оси тела, длина которого сокращается вследствие такого воздействия. Особую актуальность сжатие имеет в металлургии: в процессе ковки увеличивается прочность металла, устраняются дефекты его структуры. Взаимосвязь между величиной прикладываемой силы и деформацией сжатия зависит от вещества, из которого состоит тело и его геометрических данных – толщины и длины. В результате сжатия в теле создаётся утолщение типа «бочка».
Схематично процесс такого изменения тела представлен на рисунке 1, где F – сила.
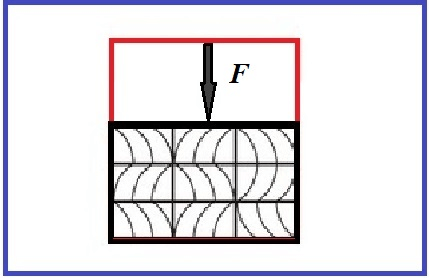
Рисунок 1. Деформация сжатия тела.
Деформация растяжения, как и сжатие, происходит в результате приложенного напряжения к оси тела, но только в обратном направлении (параллельно точкам крепления). Растяжение буксировочного троса является хорошим примером данного вида явления. В состоянии нагрузки торс, прикреплённый к буксиру и объекту буксировки, растягивается, а после её снятия – восстанавливает форму. Растяжение увеличивает длину тела и уменьшает его толщину.
Схематично данная деформация представлена на рисунке 2, где F – сила.
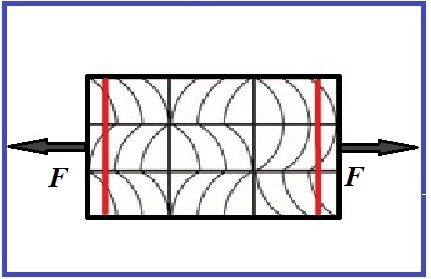
Рисунок 2. Деформация растяжения тела.
Вышеописанные простые виды деформации выражаются в изменении тела, которое можно измерить, вычислив относительную деформацию. Взяв в пример процесс растяжения, можно определить относительное удлинение путём деления абсолютного удлинения (длина в результате приложенного напряжения) на первоначальную длину тела (длина тела в состоянии покоя), что заключается в формулу ∆l= l2 — l1, где ∆l – относительное удлинение, а l2 и l1 – абсолютное и первоначальное удлинения.
Деформация сдвига является следствием воздействия на тело параллельно его основанию. Такой вид деформации выражается смещением в пространстве одной плоскости твёрдого тела относительно другой его плоскости. Расшатанный стул служит ярким примером данного вида явления, основанием в этом случае служит пол, а смещенной плоскостью (на неё же прилагается нагрузка) – сиденье.
Схематичная картина сдвига представлена на рисунке 3.
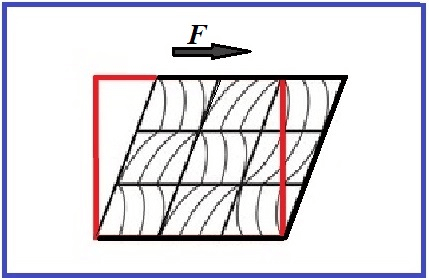
Рисунок 3. Деформация сдвига.
Относительная деформация сдвига вычисляется по формуле \[ \frac{\Delta x }{l} = \frac{1}{G}* \frac{F}{S} \], где \[\frac{\Delta x }{l}\] – искомая величина, G – модуль сдвига (коэффициент пропорциональности), F – внешняя сила, S – единица площади тела. Модуль сдвига – постоянная величина, варьирующаяся в зависимости от материала, например, у серого чугуна модуль сдвига \[4,4 *10^{4} кг / см^{2} \].
Деформация кручения создаётся действием пары сил, одна из которых вращающая, а другая – полярная, в перпендикулярной оси тела плоскости. Данный вид деформации распространяется на буровые установки, а именно их шнеки. Кручению подвергаются и всякого рода валы.
Схема деформации кручения представлена на рисунке 4.
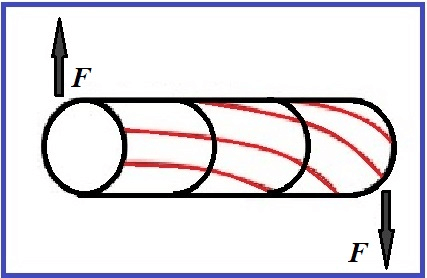
Рисунок 4. Деформация кручения.
Относительный угол закручивания определяет величину деформации и представлен отношением максимального угла закручивания к длине участка стержня. Он измеряется в радианах и ограничивается пределом, выраженным относительной величиной (условием жесткости). Важно, чтобы условия жёсткости не превосходили максимально допустимый угол закручивания, что показывает формула \[ \theta = \frac{ \varphi_{max}}{l} \leq \theta_{adm} \], где \[\theta\] – относительный угол закручивания, \[\varphi_{max}\]– максимальный угол закручивания, l – длина участка стержня, \[\theta_{adm}\] – допустимый угол закручивания.
Деформация изгиба представлена провисанием или выпячиванием оси тела, которая в состоянии покоя представляет прямую линию. Такому изменению, например, подвергаются тела, расположенные на одной опоре или нескольких. Изгиб провоцирует, как сам вес тела, так и дополнительно приложенная сила. Особую актуальность этот вид деформации приобрел в проектировании мостов, где упругость конструкции играет главную роль.
Деформация изгиба схематично представлена на рисунке 5.
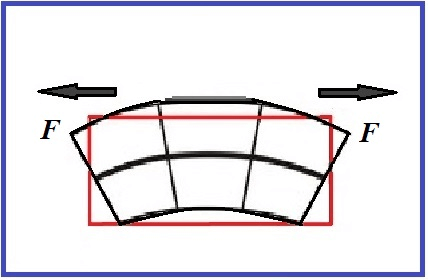
Рисунок 5. Деформация изгиба.
Если изгиб достигается только изгибающим моментом, то такая деформация называется чистым изгибом (представлен на рисунке 5), а, если добавлено действие поперечной силы в том числе, то имеет место быть поперечный изгиб. Оценить деформацию можно через формулу кривизны бруса \[ \frac{1}{p} = \frac{ M_{x} }{E J_{x} } \], где \[\frac{1}{p}\] – кривизна бруса, \[M_{x}\] – изгибающий момент, \[E J_{x}\] – жёсткость при изгибе.
Тело, подвергающееся деформированию, в зависимости от механических свойств вещества, из которого оно состоит, может по факту прекращения действия силы вернуть исходную форму, а может остаться деформированным. Первый вариант обусловлен упругостью материала, а второй – пластичностью. Так, резиновый мяч, ударившийся о землю, восстанавливает свою округлость, а шар из пластилина – нет. На способность восстановления формы телом влияет и величина действующей силы, которая может находиться в пределах прочности и превышать их, во втором случае тело разрушается.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Предел упругости и прочности
Если приложенное напряжение превысило допустимое значение, сохраняющее способность тела восстановить первоначальную форму, то после его снятия параметры тела останутся деформированными. Такой исход называется пластической деформацией, а происходит она в результате разрыва межатомных связей. Максимальное напряжение, обеспечивающее допустимую удалённость атомов, что сохраняет связь между ними, а значит и способность тела восстановить исходную форму (упругая деформация), называется пределом упругости. Величина данного показателя делит вещества на упругие и пластичные.
Возврат телу исходной формы производится под влиянием силы упругости, которая подчиняется Закону Гука, выраженному формулой \[F_{упр}=k*x \], где \[F_{упр}\] – сила упругости, \[k\] — коэффициент жёсткости, x – изменение длины тела. Формула показывает, что сила упругости находится в пропорциональной зависимости с абсолютным изменением длины деформированного тела.
Больший лимит величины, действующей на тело силы, имеет предел прочности, который представлен максимальным значением напряжения, выдерживаемым твёрдым телом, не разрушаясь. В зависимости от показателя этого предела, популярные материалы делятся на прочные и хрупкие. К первым относятся многие металлы, например, титан или хром, а хрупким считается чугун.
Относительная деформация напрямую связана с механическим напряжением тела, которое представлено отношением модуля силы к единице площади воздействия, что отражается в формуле \[ \sigma = \frac{F}{S} \], где \[\sigma\] – напряжение, \[F\] – сила, \[S\] – площадь. Механическое напряжение представлено давлением и измеряется в Паскалях. Полезность свойств материалов в виде пластичности или упругости, прочности или хрупкости заключена в его деформационных способностях в целом, и широко применяется в строительстве, машиностроении и других инженерных отраслях. Особое значение имеют упругие деформации, которые подлежат тщательному измерению тензометром – прибором, очень точно определяющим деформацию маленькой величины.














