Средняя скорость молекул

4 975

31 октября 2022 г.

Время чтения: 3 минуты

Содержание:

Что такое средняя скорость движения молекул
Как определить среднюю квадратичную скорость движения молекул

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см³ при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Определение 1

Вид формулы средней относительной скорости молекул в физике можно представить выражением:

\[\text { Vотн }=\sqrt{2} \sqrt{\frac{8 R T}{\pi m_{0}}}\]

Выражение под корнем – средняя скорость молекул идеального газа.

Как определить среднюю квадратичную скорость движения молекул

Определение 2

Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.

Средняя скорость молекул равна:

\[\left\langle\mathrm{V}_{\mathrm{KB}}\right\rangle=\sqrt{\frac{1}{N} \sum_{i=1}^{N} v_{i}^{2}}\]

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

\[\langle\mathrm{VKB}\rangle^{2}=\int_{0}^{\infty} v^{2} F(v) d v\]

Ещё одно выражение для среднеквадратичной скорости:

\[\left\langle V_{K B}\right\rangle=\sqrt{\frac{3 k T}{m_{0}}}=\sqrt{\frac{3 R T}{\mu}}\]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

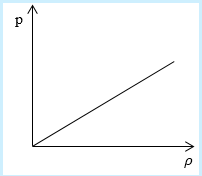
Напомним, что средняя скорость частиц:

\[\mathrm{Vcp}=\sqrt{\frac{8 R T}{\pi m_{0}}}\]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m₀= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

\[V c p=\sqrt{8 \mathrm{kT} / \pi \mathrm{m}}=\sqrt{(8 \mathrm{C} \rho / \pi \mathrm{n})(\mathrm{n} / \rho)}=\sqrt{8 \mathrm{C} / \pi}\]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

\[\left\langle\mathrm{V}_{\kappa в}\right\rangle=\sqrt{\frac{3 k T}{m_{0}}}=\sqrt{\frac{3 R T}{\mu}}\]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости \[\left\langle V_{K B}\right\rangle=\sqrt{3 \mathrm{kT} / \mathrm{m}_{0}}=\sqrt{3 \mathrm{RT} / \mu}\], получим, что средняя квадратичная скорость движения молекул газа: \[\left\langle V_{K B}\right\rangle=\sqrt{\left(3 \rho N_{a}\right) /(\mu \mathrm{n})}\]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

\[\left\langle V_{K B}\right\rangle=\sqrt{\left(3 \rho N_{a}\right) /(\mu \mathrm{n})}\]