Емкость конденсаторов
Мы все знаем об электрическом токе, проводимости и сопротивлении. Но емкость является еще одной важной частью понимания концепции электричества. Возможно, вы слышали, что ничто не может хранить электричество. Однако это не так — конденсаторы способны накапливать электрический заряд. Давайте подробнее рассмотрим концепцию конденсаторов и емкости. Начнем с конденсатора.
Конденсатор образован двумя обращенными друг к другу проводниками, между которыми вставлен диэлектрик, то есть изолирующий материал. Эти два проводника называются обкладками конденсатора.
Главной характеристикой конденсаторов является величина емкости.
Емкость конденсатора — формула
Емкость конденсатора — это ничто иное, как умение конденсатора накапливать энергию в виде электрического заряда. Другими словами, емкость — это запоминающая способность конденсатора. Измеряется емкость в фарадах.
Емкость может быть рассчитана, когда известны заряд Q и напряжение V конденсатора:
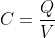
Емкость используется для описания того, сколько заряда может удерживать любой проводник. Он представляет собой отношение заряда к приложенному потенциалу.
Любой объект, который может быть электрически заряжен, показывает емкость. Конденсатор с двумя параллельными пластинами — это обычная форма накопителя энергии. Емкость отображается параллельным расположением пластин и определяется с точки зрения накопления заряда. Когда конденсатор заряжен полностью, между его пластинами имеется разность потенциалов, и чем больше площадь пластин и чем меньше расстояние между ними, тем больше будет заряд конденсатора и тем больше будет его Емкость.
Если конденсаторы соединены последовательно, формула емкости выражается следующим образом:
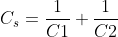
Если конденсаторы подключены параллельно, формула емкости выражается следующим образом:
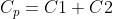
Где C1, C2, C3 ……. Cn — конденсаторы, а емкость выражается в фарадах.
Примеры решения:
Определите емкость конденсатора, если течет 5 кулонов заряда и приложен потенциал 2 В.
Решение
Приведенные параметры
Заряд Q составляет 5 C,
Приложенное напряжение V равно 2 В.
Формула емкости определяется как
C=Q/V
= 5/2
= 2,5 F
Определите емкость, если подключены конденсаторы 6 Ф и 5 Ф.
a) последовательно;
b) параллельно
Решение
Формула последовательной емкости определяется как
Cs = 1 / C1 + 1 / C2
= C1 + C2 / C1C2
= 6 + 5/30
Cs = 0,367 F
Емкость в параллельной формуле определяется как
Ср = С1 + С2
= 6 + 5
Cp = 11 F
Различают три вида конденсаторов:
- Конденсатор плоский;
- Конденсатор цилиндрический
- Конденсатор сферический.
Конденсатор плоский
Данный конденсатор образован двумя металлическими пластинами, которые мы называем A и B, расположенными на расстоянии d.

Две проводящие пластины A и B являются пластинами конденсатора, d — их расстояние, более того, поскольку две пластины параллельны, их поверхности равны.
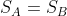
Мы знаем, что внутри двух поверхностей электрическое поле однородно, а снаружи равно нулю
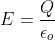
Рассчитываем разность потенциалов между двумя пластинами
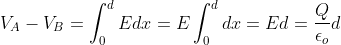
Как только разность потенциалов известна, мы можем рассчитать емкость плоского конденсатора.
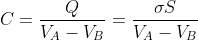
Заменим найденную ранее разность потенциалов
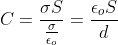
Конденсатор цилиндрический
Конденсатор используется для хранения большого количества электрического тока в небольшом пространстве. Цилиндрический конденсатор включает полый или сплошной цилиндрический проводник, окруженный концентрическим полым сферическим цилиндром. Конденсаторы широко используются в электродвигателях, мельницах, электрических соковыжималках и других электрических инструментах. Разность потенциалов между конденсаторами различна. Существует множество электрических цепей, в которых конденсаторы должны быть сгруппированы соответствующим образом, чтобы получить желаемую емкость. Есть два общих режима, включая конденсаторы, включенные последовательно, и конденсаторы, подключенные параллельно. Единица измерения емкости — Фарад (Ф).
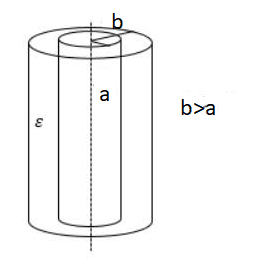
Его часто используют для хранения электрического заряда. Цилиндрический конденсатор — это тип конденсатора, который имеет форму цилиндра, имеющую внутренний радиус как a и внешний радиус как b.
Формула для цилиндрического конденсатора:
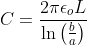
C = емкость цилиндра
L = длина цилиндра
a = внутренний радиус цилиндра,
b = внешний радиус
εₒ= диэлектрическая проницаемость свободного пространства (8.85×10ˉ¹²)
Цилиндрический конденсатор длиной 8 см состоит из двух колец с внутренним радиусом 3 см и внешним радиусом 6 см. Найдите емкость конденсатора.
Дано:
Длина L = 8 см
внутренний радиус a = 3 см
внешний радиус b = 6 см
Решение
Формула для конденсатора цилиндрического:
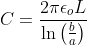
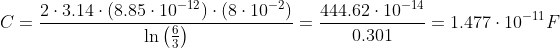
Конденсатор сферический
Данный конденсатор состоит из сплошного или полого сферического проводника, окруженного другой полой концентрической сферической формой другого радиуса.
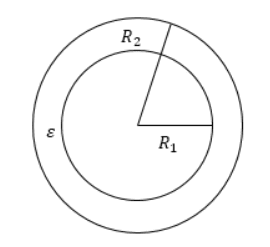
Формула для определения емкости сферического конденсатора
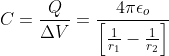
Где,
C = емкость
Q = заряд
V = напряжение
r 1 = внутренний радиус
r 2 = внешний радиус
ε 0 = диэлектрический потенциал (8,85 x 10-12 Ф / м)
Значение емкости двух разных конденсаторов может быть одинаковым, а номинальное напряжение двух конденсаторов может быть разным. Возьмем два конденсатора — один с малым номинальным напряжением, а другой с высоким. Если мы заменим конденсатор с меньшим номинальным напряжением на конденсатор с более высоким номинальным напряжением, то получится конденсатор меньшего размера. Это может произойти из-за неожиданного повышения напряжения.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Влияние диэлектрика на емкость
Плотности поверхностного заряда равны σ p и — σ p. Когда мы полностью помещаем диэлектрик между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.
Внутри конденсатора следующее электрическое поле:
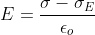
Следовательно, мы имеем:
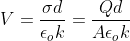
а именно:
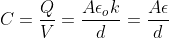
Ɛ — диэлектрическая проницаемость. Разность потенциалов между пластинами задаются
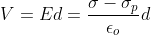
Для линейных диэлектриков:
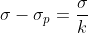
Где k — диэлектрическая проницаемость вещества, K = 1.
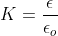
Электрическое поле между пластинами конденсатора прямо пропорционально емкости конденсатора. Напряжение электрического поля снижается из-за наличия диэлектрика. Если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора. Таким образом, диэлектрик увеличивает емкость конденсатора.














