Формула для расчета линейной скорости
Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.
Понятие скорости
Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.
Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.
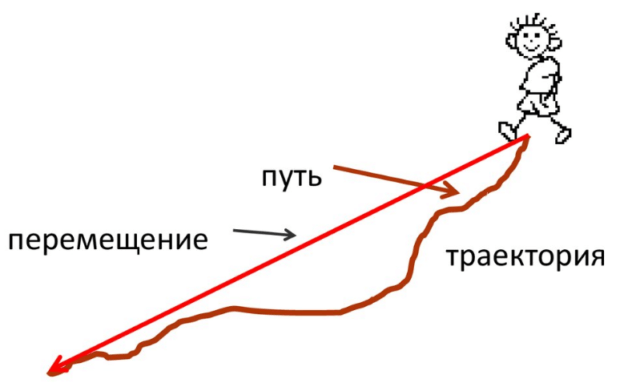
Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.
Формула понятия скорости следующая:
\[\overline{\mathrm{v}}=s / t\]
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Из приведённой формулы очень легко найти размерность скорости. Т. к. расстояние измеряется в метрах, а время в секундах, то единицей скорости будет метр в секунду м/с. Отметим, что на практике часто скорость измеряют не в метрах в секунду, а, например, в километрах в час.
Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.
Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.
Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
Словосочетание «проезжает тоннель за 3 минуты» означает, что это время поезд входит в тоннель кабиной машиниста и выходит с концом последнего вагона. Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
\[S = I + L = 300 + 420 = 720 м/с.\]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.
Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.
Ответ: Скорость поезда равна 4 м/с.
Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.
Решение:
Обозначим время движения машины со скоростью 4 км/ч, как \[t_{1}\], а время движения машины со скоростью 61,2 км/ч, как \[t_{2}\].
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как \[S_{1}\], он равен \[S_{1}\] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: \[S_{2} = 4*61,2 = 244,8 км\]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Это есть весь путь, пройденный нашей машиной.
Общее время t, которое она потратила будет \[t = t_{1} + t_{2} =3 + 4 = 7 ч\]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.
Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.
Линейная скорость
Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.
Формул для расчета линейной скорости существует множество, но общей можно назвать:
\[v=S / t\]
S – путь, который прошло тело, t – время, которое оно на это потратило.
Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
О связи между линейной и угловой скоростями
Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения.
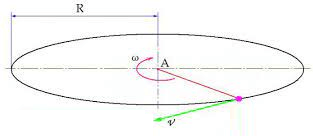
Обозначается она буквой ω. Формула нахождения угловой скорости следующая:
\[\overline{\omega}=\phi / t\],
где ϕ – угловое перемещение, t – время.
Измеряется угловая скорость в радианах в секунду рад/с.
Теперь о связи между линейной и угловой скоростью. Из формулы\[\boldsymbol{v=2 \pi R / T}\] следует, что v также будет равно v = 2πRν, где ν – частота вращения точки. Отсюда легко понять, что v = ωR.
Линейная скорость и ускорение при движении по окружности
Центростремительное ускорение движущейся равномерно по окружности точки вычисляется по формуле:
\[a=v^{2} / R\]
Оно связывает линейную скорость и ускорение. Исходя из связи линейной и угловой скоростей можно получить:
\[a=\omega^{2} R\]
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике