Формула центростремительного ускорения в физике
Что такое центростремительное ускорение
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Чему равно центростремительное ускорение
Модуль центростремительного ускорения определяется формулой:
Модуль an остается постоянным, однако направление вектора an все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
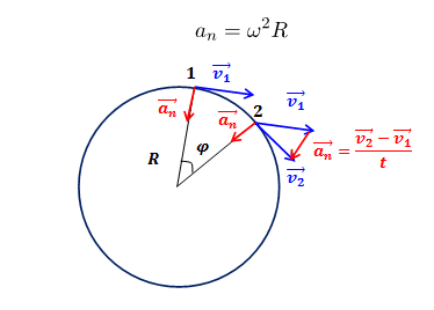
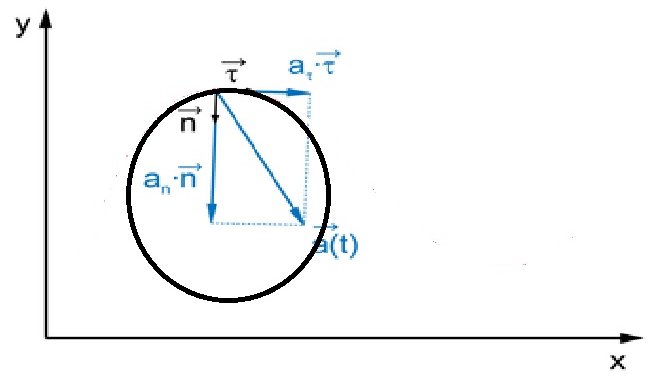
В общем случае ускорение движущейся по окружности точки можно представить в виде двух составляющих – нормальной и тангенциальной. Первая составляющая направлена по касательной к траектории, вторая по радиусу непосредственно к центру круга. Всё это можно представить в виде формулы:
Где R – радиус окружности, n – единичный вектор нормали к траектории.
Тангенциальное ускорение
Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c2. Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нормальное или центростремительное ускорение
Это вторая составляющая разложенного нами движения (v2/R)*n. Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v2*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.
n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид an = (ω*R)2/R = ω2*R.
Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c2.
Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.
Примеры решения задач
Задача №1.
Поезд движется со скоростью 54 километра в час по закруглению, радиус которого равен 1 километру.
Найти чему равно его центростремительное ускорение.
Дано:
Радиус R = 1 км = 1000 м.
Скорость v = 54 км/ч = 15 м/с.
Найти нужно нормальное ускорение \[a_{n}\].
Решение:
Формула центростремительного ускорения в физике нам известна \[a_{n}=v^{2} / R\]. Подставляем в неё наши
числовые значения и находим \[a_{n}=(15 м/с)^{2} / 1000=0,225 м/
с^{2}\].
Ответ: \[a_{n}=0,225 м/с^{2}\].
Задача №2.
Тело движется по траектории радиусом 5 метров с угловой скоростью 0,3 радиан в секунду. Требуется найти его
центростремительное ускорение.
Дано:
Радиус R = 5 м.
Угловая скорость \[\omega=0,3 \text { рад/с }\]
Найти центростремительное ускорение \[a_{n}\].
Решение:
Опять подставляем числовые значения, но уже в формулу \[a_{n}=\omega^{2} * R\].
\[a_{n}=5^{2 *} 0,3=0,45 м/с^{2}\].
Ответ: \[a_{n}\] равно \[0,45 м/с^{2}\]
Задача №3.
Диск вращается вокруг неподвижной оси. Угол поворота диска изменяется в соответствие с уравнением ϕ = 5t+7.
Нужно вычислить, чему равно центростремительное ускорение очки диска, расположенной на расстоянии R от оси
вращения равном 0,5 м на 4 секунду от времени начала вращения.
Дано:
Радиус R = 0,5 м.
Время t = 4 c.
Закон движения ϕ = 5t+7 .
Найти \[a_{n}\].
Решение:
Формула центростремительного ускорения, включающая угловую скорость \[a_{n}=\omega^{2 *} R\].
Угловую скорость можно найти по формуле \[\omega=d \phi / d t\].
Подставляем вместо ϕ уравнение изменения угла поворота \[\omega=d(5 t+7) / d t\].
Производная этого выражения равна 10t.
Теперь нужно подставить вместо t конкретное числовое значение, т.е. 4 секунды.
Получаем \[a_{n}=10 * 4=40 м/с^{2}\].
Ответ: \[a_{n}\] точки на диске равно \[40 м/с^{2}\].
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике