Сила упругости, закон Гука
При воздействии на какое-то тело определенной силы данное тело в ответ будет сопротивляться и стараться принять свою первоначальную форму. Это можно объяснить тем, что в теле происходит электромагнитное воздействие молекул.
Под давлением приложенной силы тело начинает гнуться и происходит деформация, которая обусловлена перемещением частиц тела друг относительно друга и расстояния между атомами. Деформация и сила упругости напрямую зависят друг от друга, если не будет деформации, то и сила упругости перестает действовать.
Сопротивляемость тела к воздействующему к нему силе характеризует его жесткость, способствующее упругости против приложенной нагрузки.
Сила упругости — сила, обратного воздействия тела при деформации формы и размера, которое старается вернуть его в первоначальное состояние.
- Существуют различные виды деформаций, как простых, так и сложных:
- Растяжение
- Сжатие
- Кручение
- Изгиб
- Также подразделяются на
- Обратимые
- необратимые
Приведем простейший пример деформации и возникновения силы упругости по закону Гука.
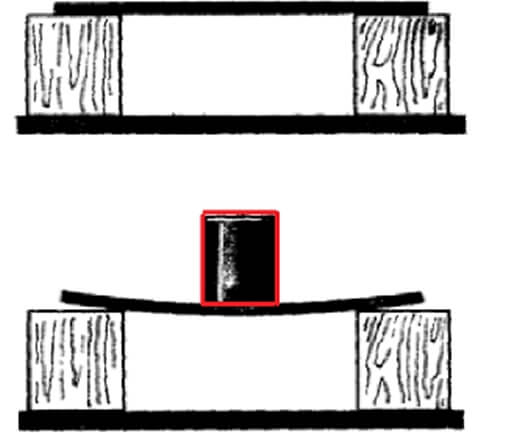
Если на середину доски, установленной на двух опорах, положить груз, то под воздействием веса силы тяжести, доска будет продавливаться до определенного момента и остановится под воздействием силы упругости действующей против силы тяжести. Сила упругости по закону Гука равна силе созданной жесткостью тела к изменению его длины.
Сила упругости, закон Гука, вес тела
Британский физик XVII века Роберт Гук, внес огромный вклад в изучении силы упругости, открыв впервые в 1667 году, закон пропорциональности между силой, приложенной к упругому телу и его деформацией который гласит:
Физическая сила упругости по закону Гука, объясняет о том, что сила возникшая при растяжении и сжатии тела, пропорциональна его удлинению.
Формула силы упругости по закону Гука:
\[F(упр) = kx\]
Где: x — изменение длины тела, k — коэффициент жесткости тела — силы упругости закона Гука.
Каждое тело имеет свою жесткость, от которого зависит изменение его длины под действием определенной силы. В международной системе измерения Си единицей жесткости является ньютон на метр (1Н/м).
Вторая формула по закону Гука выражена через относительную деформацию:
\[\varepsilon=x / \mid\] и напряжение тела \[\sigma=-(\text { Fупр/ S) }\]
Где: S — площадь поперечного сечения деформированного тела.
\[\varepsilon=\sigma \mathrm{E} \varepsilon=\sigma \mathrm{E}\]
Где: E — модуль Юнга, величина которая зависит только от свойства материала и не зависит от формы и размера тела.
Модуль Юнги для разных материалов имеет различные значения, например,
- для стали E ≈ 2 ⋅ 10 11 Н / м 2 E≈2·1011 Нм2
- для резины E ≈ 2 ⋅ 10 6 Н / м 2

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
График силы упругости
Закон Гука и график силы упругости можно выразить зависимостью между величинами силы упругости и удлинением пружины Fупр=k⋅Δl.
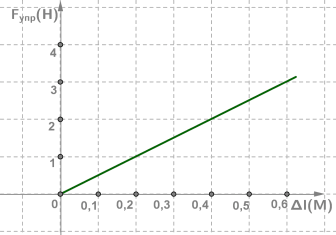
В интернете можно найти много примеров связанных с решением задач по теме сила упругости по закону Гука, различных материалов. С помощью формул и справочных данных по различным материалам легко решить различные задачи по вычислению силы упругости по закону Гука.
Задача на расчет силы упругости
Условие: Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение: Запишем закон Гука: По третьему закону Ньютона:
Ответ: 10 кН.














