Удельное сопротивление
Некоторые вещества в природе (как металлы, так и неметаллы) являются проводниками электрического тока. При движении тока в них тока, вещества оказывают сопротивление его прохождению. Физическая величина, которая определяет способность материала препятствовать прохождению через него электрического тока называется удельным сопротивлением.
Металл с небольшим значением этого параметра – медь. Низкое значение сопротивления движению тока \[\left(0,017 \frac{O м * мм^{2}}{м}\right)\] позволяет использовать медь в качестве проводника.
Описанная величина обозначается греческой буквой «ро» – ρ.
Формула удельного сопротивления
Для расчета данного параметра немецким физиком Георгом Омом была выведена формула удельного сопротивления:
\[\boldsymbol{R=\frac{\rho * l}{S}}\]
Эта формула записана относительно сопротивления. Для того чтобы вывести значение данной физической величины, необходимо преобразовать исходную формулу:
\[\frac{\rho * l}{S}=R\]
сперва нужно умножить обе части уравнения на S:
\[\frac{\rho}{S}=\frac{R}{l}\]
затем l переносится в правую часть:
\[\rho=\frac{R * S}{l}\]
Исходя из полученного выражения, можно сформулировать понятие удельного сопротивления: препятствие данного вещества единичной длины и единичной площади поперечного сечения движению тока.
Получившаяся формула используется для нахождения значения исследуемого параметра. Кроме искомой величины, в формуле фигурируют ещё три члена:
- R – сопротивление, измеряемое в Ом;
- l – длина проводника, в метрах;
- S – площадь поперечного сечения, мм².
В общепринятой международной системе (СИ) единицей измерения удельного сопротивления является Ом*м. При решении практических задач, полученные значения чаще всего выражают в \[\frac{O_{\mathrm{м} * \mathrm{мм}^{2}}}{\mathrm{м}}\].
Для большинства часто применяемых металлов этот параметр уже рассчитан. Ниже представлена таблица 1, в которой собраны значения величины для некоторых металлов.
| Металл | Числовое значение удельного сопротивления при температуре \[20C^{\circ}\], \[\frac{O_{м * м м^{2}}}{м}\] |
| Медь | 0,017 |
| Серебро | 0,016 |
| Вольфрам | 0,055 |
| Золото | 0,024 |
| Алюминий | 0,028 |
| Железо | 0,1 |
| Свинец | 0,21 |
Зависимость удельного сопротивления от температуры
В приведенной таблице отмечено, что указанные значения приводятся при температуре \[20C^{\circ}\]. Действительно, удельное сопротивление зависит от температуры. Но для каждого материала влияние температуры внешней среды будет разным. Такое явление обусловливается температурным коэффициентом \[(\alpha)\]. Он учитывается при расчете параметра по формуле: \[\rho_{t}=\rho_{0} *\left[1+\alpha *\left(t_{1}-t_{o}\right)\right]\].
В этом выражении представлены значения:
- \[\rho_{0}\] – удельного сопротивления металла при температуре окружающей среды \[20 C^{o}\];
- α – температурного коэффициента;
- t1 – t0 – разница температур (Δt).
Данная формула устанавливает зависимость удельного сопротивления от температуры.
В таблице 2 приведены числовые значения температурного коэффициента для некоторых металлов.
| Металл | Температурный коэффицент сопротивления \[\alpha, K^{-1}\] |
| Алюминий | 0,0049 |
| Вольфрам | 0,0045 |
| Медь | 0,0039 |
| Никель | 0,0050 |
| Олово | 0,0042 |
| Ртуть | 0,0009 |
| Серебро | 0,0036 |
Примеры расчета удельного сопротивления
Используя приведенную формулу, можно рассчитать значения удельного электрического сопротивления с учетом температурного коэффициента.
Необходимо рассчитать числовое значение исследуемой величины для вольфрама при температурах 50 и -50 градусов Цельсия.
Применяем полученную формулу для расчетов при 50-ти градусах:
\[\begin{gathered}
\rho_{t}=\rho_{0} *\left[1+\alpha *\left(t_{1}-t_{0}\right)\right]=0,055 *[1+0,0045 *(50-20)]=0,0624 .
\end{gathered}\]
По этой же формуле произведем расчет при температуре -50 градусов:
\[\begin{gathered}
\rho_{t}=\rho_{0} *\left[1+\alpha *\left(t_{1}-t_{0}\right)\right]=0,055 *[1+0,0045 *(-50-20)]=0,0376 .
\end{gathered}\]
Исходя из примеров расчета удельного сопротивления, можно сделать вывод, что с увеличением температуры внешней среды растет удельное сопротивление.
На рисунке представлен график зависимости удельного сопротивления от температуры.
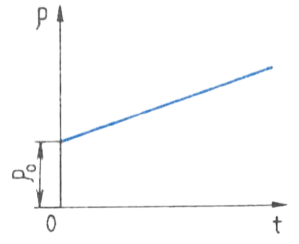
График наглядно показывает рост этой физической величины в процессе повышения температуры.
Применение формул на практике
На практике часто приходится производить расчет по той причине, что материал изделия неизвестен. Это обстоятельство лишает возможности обратиться к справочной литературе за необходимыми данными.
При расчете искомого параметра понадобятся не только теоретические формулы, но и специальные приборы: мультиметр и микрометр.
Дан пруток, имеющий длину 5 метров. При помощи штангенциркуля определим диаметр сечения. Полученное значение составило 0,42 мм.
Площадь сечения определяется по формуле:
\[\boldsymbol{S=\frac{\pi * d^{2}}{4}}\]
Затем необходимо измерить электрическое сопротивление материала. Мультиметр показывает 45 Ом.
Подставим площадь в исходную формулу для расчета искомой величины:
\[\begin{gathered}
\rho=\frac{R * S}{l} \\
\rho=\frac{R * \pi * d^{2}}{4 * l}
\end{gathered}\]
Далее подставим полученные значения в формулу и рассчитаем искомый параметр:
\[\rho=\frac{45 * 3,14 * 0,42^{2}}{4 * 5}=1,24 \frac{O м * \cdot мм^{2}}{м}\]
Полученное значение необходимо сверить со справочником. Учитывая несовершенство приборов, и возникшие в процессе непосредственного измерения размеров изделия погрешности, можно сделать вывод, что пруток изготовлен из нихрома.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Понятие проводимости
Физическая величина, которая характеризует возможность материала проводить электрический ток, называется проводимостью (электропроводностью). Единицей измерения этой величины в системе СИ служит Сименс (См).
Проводимость является величиной, обратной к электрическому сопротивлению.
Соотношение между удельным сопротивлением и удельной электропроводностью можно представить в виде:\[\sigma=\frac{1}{\rho}\]
Электропроводность материала определяется способностью заряженных частиц (ионов и электронов) свободно перемещаться в пределах данной среды. Из этого можно сделать вывод, что проводимость зависит от нескольких характеристик материала:
- строения вещества;
- химического состава;
- агрегатного состояния.
Кроме того, поскольку удельное сопротивление зависит от температуры, то и проводимость тоже будет зависеть от этого фактора.
Ниже представлена таблица 3, в которой показаны значения проводимости для основных металлов.
| Металл | Значение проводимости *107, См/м |
| Серебро | 6,2 |
| Медь | 5,8 |
| Золото | 4,52 |
| Алюминий | 3,77 |
| Вольфрам | 1,9 |
| Латунь | 1,55 |
| Железо | 0,99 |
Стоит отметить, что указанные в данной таблице значения реальны только при температуре 25 градусов Цельсия. С изменение температуры, электропроводность материалов будет изменяться. На основании приведенной выше зависимости удельного сопротивления от температуры и, руководствуясь формулой для расчета проводимости, можно сделать вывод, что с увеличением температуры окружающей среды значение проводимости будет снижаться.
Проводимость серебра выше проводимости меди. Однако серебро не получило широкого промышленного распространения в качестве проводника электричества, поскольку имеет высокую стоимость.
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике