Первый закон термодинамики
Термодинамикой называют науку, изучающую природные явления, которые сопровождаются передачей теплоты. Объектом изучения термодинамики является термодинамическая система. Термодинамика базируется на экспериментально установленных истинах, представленных в виде законов (начал).
На рисунке 1 схематично изображены потоки энергии, перемещающиеся между выделенной системой и окружающей средой. При движении теплового потока к термодинамической системе величина количества теплоты (Q) принимает значения больше нуля. В случае, если система совершает работу над внешними телами, выполняется неравенство A>0.
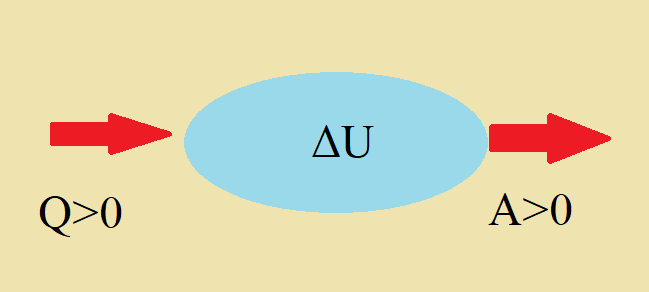
Протекание теплообменных процессов между окружающей средой и отдельно взятой системой сопровождается изменением её параметров:
- температуры;
- давления;
- объёма.
Зависимость внутренней энергии от указанных параметров приводит к её изменению при обмене теплом или совершении работы (\[\Delta U\]).
Формулировка первого закона термодинамики
Первый закон термодинамики представляет собой количественное выражение закона сохранения энергии. Он учитывает изменения внутренней энергии и теплообмен.
Математическая формула первого закона термодинамики выглядит следующим образом:
\[\Delta U=Q-A\]
На основании представленной формулы, формулировка первого закона термодинамики будет звучать так: процесс возникновения или исчезновения энергии невозможен – энергия системы при всех её изменениях сохраняет постоянную величину. Из представленного определения можно сделать вывод, что создать вечный двигатель первого рода невозможно. Это такой двигатель, полезная работа которого превышает подведенное к нему количество энергии.
При этом в истории человечества было немало попыток создать вечный двигатель, но ни одна из них не достигла успеха.
Математика позволяет записать уравнение первого закона термодинамики относительно количества теплоты:
\[Q=\Delta U+A\]
В таком случае возможно сформулировать закон по-другому: полученное системой количество теплоты направлено на изменение её внутренней энергии и совершение работы над окружающими объектами.
Положения первого закона термодинамики имеют доказательную базу, основанную на проведенных экспериментах. Первое начало термодинамики доказывает невозможность возникновения энергии из ниоткуда, так же, как и её бесследное исчезновение. Энергия передается между системами и изменяет свои формы в процессе передачи.
Невозможность создания вечного двигателя – ещё одно следствие первого начала. Такое утверждение следует из первого и второго законов термодинамики.
Применение первого закона термодинамики
Процессы, при протекании которых один из параметров газа остается постоянным, называются изопроцессами. Практическое применение первого закона термодинамики отражено в описании этих процессов.
Изохорный
При протекании изохорного процесса объем вещества остается постоянным (\[V=c o n s t\]). Для реализации изохорного процесса можно нагревать или охлаждать газ, находящийся в замкнутом сосуде постоянного объема.
В случае, если объем вещества остается постоянным, его работа равна нулю (A=0), то есть газ не совершает работу.
Для изохорного процесса справедлива формула:
\[Q=\Delta U=U\left(T_{2}\right)-U\left(T_{1}\right)\]
Члены данного уравнения \[U\left(T_{1}\right)\] и \[U\left(T_{2}\right)\] – это внутренние энергии газа при исходной температуре и в конце процесса соответственно. Закон Джоуля устанавливает, что внутренняя энергия газа зависит только от температуры.
Если температура газа повышается при постоянном объеме, происходит его нагревание и система поглощает тепло (Q < 0), что приводит к увеличению внутренней энергии. В случае охлаждения газа, тепло отдается во внешнюю среду (Q < 0).
Изобарный
Изобарный процесс характеризуется постоянством давления (\[p=c o n s t\]). Работа газа, совершаемая над внешними объектами, будет определяться по формуле:
\[A=p\left(V_{2}-V_{1}\right)=p \Delta V\]
Уравнение первого закона термодинамики при изобарном процессе примет вид:
\[Q=U\left(T_{2}\right)-U\left(T_{1}\right)+p\left(V_{2}-V_{1}\right)=\Delta U+p \Delta V\]
Изобарное расширение сопровождается поглощением газом тепла (Q>0), а его работа принимает значения больше нуля. Если происходит сжатие при постоянном давлении, то тепло отдается окружающей среде, а работа над внешними объектами отрицательна (A<0). Конечная температура в процессе сжатия будет меньше исходной. Внутренняя энергия уменьшится (\[\Delta U<0\]).

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Изотермический
Изотермический процесс осуществляется без изменения температуры газа (\[T=C o n s t\]). Закон Джоуля устанавливает, что внутренняя энергия зависит только от температуры. Поскольку температура рабочего тела сохраняется постоянной при изотермическом процессе, изменение внутренней энергии равно нулю (\[\Delta U=0\]).
Для изотермического процесса первый закон термодинамики записывается так:
\[Q=A\]
Исходя из формулы, можно сделать вывод, что подведенное к системе количество теплоты при изотермическом расширении затрачивается на внешнюю работу газа. При изотермическом сжатии происходит обратный процесс – работа внешних сил, совершенная над рабочим телом, переходит в теплоту, которая передается окружающей среде.
Адиабатный
Все описанные выше процессы отличает наличие теплообмена с внешней средой. Однако в физике изучаются процессы, которые происходят без теплового обмена системы и окружающих предметов.
Примером может служить адиабатный процесс, который тоже является изопроцессом. Он протекает в пределах так называемой адиабатической оболочки. Она представляет собой сосуд, стенки которого непроницаемы для тепловых потоков.
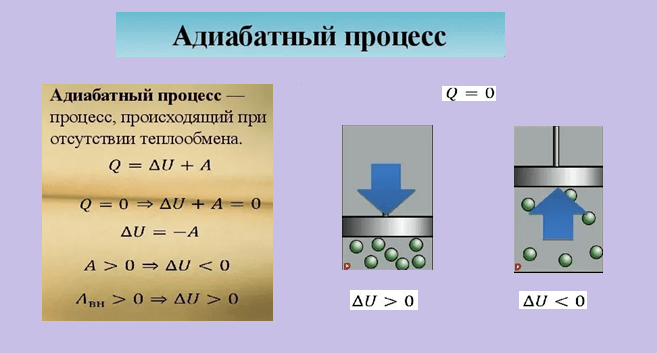
Числовое значение количества теплоты при адиабатном процесс равняется нулю (\[Q=0\]).
С учетом этой особенности, уравнение первого закона термодинамики запишется в виде:
\[A=-\Delta U\]
Из полученной формулы делается вывод, что совершение работы газом происходит за счет уменьшения внутренней энергии.
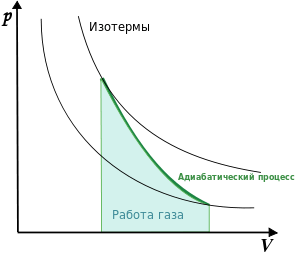
На рисунке 3 в системе координат давления и объема (\[p, V\]) в виде кривой – адиабаты представлен график процесса.
При адиабатном расширении совершаемая газом работа принимает положительные значения (A>0), а изменение внутренней энергии будет отрицательным (\[\Delta U<0\]). При этом температура системы снижается.
Уравнение адиабаты для идеального газа в термодинамике имеет вид:
\[p V^{\gamma}=\text { const }\]
Здесь γ – показатель адиабаты, рассчитывающийся по формуле:
\[\gamma=\frac{C_{p}}{C_{V}}\]
Члены уравнения \[C_{p}\] и \[C_{v}\] называются теплоемкостями газа при постоянных давлении и объёме соответственно. Показатель адиабаты может принимать несколько разных значений:
- \[\gamma=1,67\]– для одноатомного;
- \[\gamma=1,4\]– для двухатомного;
- \[\gamma=1,3\]– для многоатомных газов.
Работа газа над внешними объектами в описываемом процессе определяется из формулы:
\[A=C_{V}\left(T_{2}-T_{1}\right)\]
В этом выражении \[T_{2}\] и \[T_{1}\] – конечная и начальная температуры.
Энтропия
Энтропия отражает результат спонтанных изменений, происходящих в системе. Энтропия – это степень неупорядоченности.
Изменение энтропии – величина, эквивалентная полученной системой теплоте \[\left(\frac{\Delta Q}{T}\right)\], а поскольку изменения количества теплоты не происходит ни на одном из участков адиабатного процесса (\[\Delta Q=0\]), энтропия в этом процессе остается постоянной.
Все изопроцессы квазистатические. Это значит, что они протекают с бесконечно малой скоростью и представлены в виде бесконечного числа равновесных состояний.
Но адиабатные процессы не всегда являются квазистатические, поскольку они протекают в изолированной системе.
Одна из характеристик квазистатического процесса – обратимость. Примером неквазистатического (необратимого) процесса может служить расширение газа в пустое пространство.
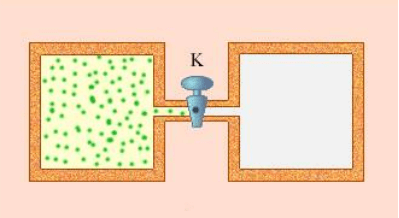
На рисунке 4 изображена адиабатная оболочка, представленная в виде двух камер, соединенных проводящей трубкой. Трубка закрыта вентилем. В одной из камер находится газ, в другой – вакуум. При открытии задвижки газ начнет заполнять все предоставленное пространство. В итоге обе камеры окажутся заполненными, а состояние системы вновь станет равновесным.
Поскольку протекающий процесс адиабатный, теплообмен с окружающей средой исключен, значит Q=0. Газ не совершает работы над внешними телами, поскольку находится в пределах недеформируемого сосуда. Внутренняя энергия рабочего тела не изменяется, исходя из первого закона термодинамики (\[\Delta U=0\]). Поскольку изменение внутренней энергии определяется непосредственно изменением температуры газа, можно сделать вывод, что температура в начале процесса равна температуре в конце.
Точки двух этих положений на графике будут находиться на одной изотерме. Что касается состояний, в которых находился газ между двумя этими точками, то все они не равновесны и их нельзя показать в плоскости p — V.
Процессы первого закона термодинамики
Для более наглядного представления об описанном применении первого закона термодинамики к изопроцессам можно обобщить основные сведения о них в таблице 1.
| Процесс | Константа | Уравнение |
| Изохорный | \[V=c o n s t\] | \[Q=U\left(T_{2}\right)-U\left(T_{1}\right)\] |
| Изобарный | \[p=\text { const }\] | \[Q=\Delta U+p \Delta V\] |
| Изотермический | \[T=c o n s t\] | \[Q=A\] |
| Адиабатный | \[Q=c o n s t\] | \[A=-\Delta U\] |














