Теплообмен. Уравнение теплового баланса
Термодинамика — это одна из основных частей физики. Она применяется в таких отраслях как: гидродинамика, аэродинамика, оптика, физическая химия и другие прикладные разработки.
Возникновение термодинамики относят к 19 веку, ведь именно в этот момент начала развиваться теплотехника. А термодинамика является ее теоретической основой.
Содержание современное термодинамики:
Изучение законов тепловой формы движения материи и все связанные с этим явления.
Цель термодинамики — это изучение общих закономерностей преобразования энергии.
При этом обязательно учитывается внутренняя энергия тел (Q ) , а именно ее изменение.
При этом меняться она может двумя способами:
- Совершение работы над системой. То есть преобразования механической энергии во внутреннюю энергию.
- Передача тепла — теплообмен.
Количество теплоты, которая была получена телом
В процессе теплообмена изменение внутренней энергии тела, это ни что иное как результат работы внешних сил. Однако это не та работа, которая связана со сменой внешних параметров системы, а работа производится благодаря молекулярным силам.
Соприкосновение тела и горячего газа. При таком взаимодействии через столкновение молекул тела с молекулами газа происходит передача энергии газа.
Мера измерения, которая применяется в процессе теплообмена при изменении внутренней энергии тела выступает количество тепла (Q).
Виды теплообмена:
- теплопроводность;
- конвекция (конвективный теплообмен);
- излучение (теплообмен при помощи излучения).
Рассмотрим пример с помощью рисунка теплообмена ниже.
Есть два тела:
Одно имеет более высокую температуру и второе — низкую температуру.
Первое будет остывать и отдавать тепловую энергию до тех пор, когда температура двух тел не станет идентичной. Это будет называться тепловым равновесием взаимодействующих тел.
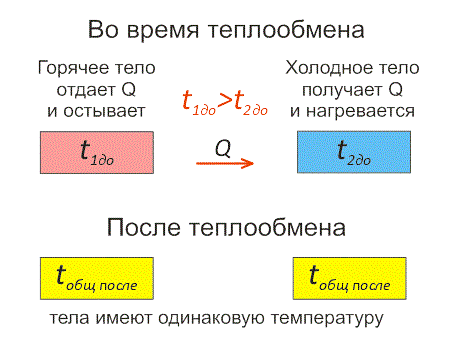
Когда работ в системе не совершается, но при этом к ней проводится тепло. При таком раскладе в соответствии с законом сохранения энергии (первым началом термодинамики) все тепло, которое будет передано системе, идет на увеличение внутренней энергии системы:
\[\Delta Q=\Delta U \text { (№1) }\]
В этом случае, \[\triangle U\] каждого тела при нагревании будет равняться массе тела (m) умноженной на удельную теплоемкость вещества (c) и умноженное на изменение температуры тела \[(\triangle T)\].
\[\Delta U=m c \Delta T(\text { №2) }\]
При плавлении и кристаллизации для расчета \[\triangle U\] будет использована следующая формула:
\[\Delta U=\pm \lambda m \text { (№3) }\]
\[\lambda-\] удельная теплота плавления или кристаллизации вещества.
m — масса тела.
Для определения при конденсации или парообразования применяем:
\[\Delta U=\pm r m \text { (№4) }\]
r — удельная теплота конденсации или парообразования.
m — масса тела.
При этом не следует забывать, что все вышеупомянутые процессы: плавление, кристаллизация, конденсация, парообразование происходят без изменения температуры, то есть при постоянной температуре.
По изложению формул под номерами три и четыре, мы можем ясно увидеть, что изменение внутренней энергии системы не зависит от температуры.
Когда топливо полностью подлежит сгоранию выделяется теплота, которую можно определить с помощью следующей формуле:
\[\Delta Q=\Delta U=q m \text { (№5) }\]
q — удельная теплота сгорания топлива.
m — масса тела.
Сохранение тепловой энергии и уравнение теплового баланса
При остывании одного тела, происходит отдача тепловой энергии, то есть теплообмен с окружающей средой. Утерянная теплота Q будет иметь знак “минус”.
При нагревании тела — оно получает тепловую энергию. И та приобретенная теплота Q будет иметь знак “плюс”.
В изолированной системе может происходить только теплообмен. Один из главных законов в физике, а именно в термодинамике, является закон сохранения и превращения энергии.
В том случае, когда в системе, которая изолирована, не происходит никаких процессов превращений кроме теплообмена, количество теплоты, которая будет отдана телами (их внутренняя энергия будет уменьшаться) будет равна количеству тепла полученного телами (их внутренняя энергия будет увеличиваться). Но не смотря на процесс теплообмена, общая -суммарная энергия системы будет неизменна и мы сможем записать первое начало термодинамики с помощью формулы:
\[\Delta U=\sum_{i=1}^{n} \Delta U_{i}=0(\mathrm{№} 6)\]
Это и является уравнением теплового баланса.
Также можно его выразить иначе. Общее количество тепла, которое выделилось в изолированной системе будет равное суммарному количеству тепла, которое было поглощено в системе. Записать это можно в следующем виде:
\[Q_{1}+Q_{2}+Q_{2}+\ldots+Q_{n}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{2}^{\prime}+\ldots Q_{k}^{\prime} \text { (№7). }\]
Если брать смысл теплового баланса, он заключается в сохранении энергии для процессов, связанных с теплообменом в термоизолированных системах.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример теплообмена между холодным и горячим телом
В горячую воду с температурой +80 градусов Цельсия, которая имеет массу двести грамм, добавили охлажденную воду, имеющею температуру +15 градусов Цельсия с массой сто грамм.
Вопрос:
Какая температура будет у смешанной воды после того, как произойдет тепловое равновесия?
Примечание: не учитывать теплообмен с окружающей средой.
В данном случае, мы с вами рассмотрим упрощенную задачу, для лучшего понимания закона сохранения энергии. В данной задаче, мы не будем учитывать осуществляемый теплообмен с емкостью, которая наполнена водой.
Решение:
Считаем систему изолированной, так как в условии было сказано, что окружающая среда не будет участвовать в теплообмене.
Из-за того, что теплообмен с окружающей средой и воздухом происходить не будет, вся тепловая энергия, которую получит холодная вода, будет отдана горячей водой
- Записываем уравнение теплового баланса:
\[Q_{\text {остывания горячей воды }}+Q_{\text {нагревания холодной воды }}\] - Записываем формулу для каждого количества теплоты:
\[Q_{\text {остывания горячей воды }}=\mathrm{C}_{\text {воды }}^{*} m_{\text {горячей воды }} *\left(t_{\text {общ }}-t_{\text {горячей воды }}\right)\]
\[Q_{\text {нагревания холодной воды }}=\mathrm{C}_{\text {воды }}^{*} m_{\text {холодной воды }}^{*}\left(t_{\text {общ }}-t_{\text {холодной воды }}\right)\]
Примечания:
- \[c_{воды}\] — берем из справочника
- Массу воды обязательно переводим в килограммы
- Разность \[\left(t_{\text {общ }}-t_{\text {горячей воды }}\right)\] будет с отрицательным знаком, потому что ее окончательная температура будет меньше ее изначальной.
- Подставляем выражения и выводим окончательную формулу:
\[c_{\text {воды }} * m_{\text {горячей воды }} *\left(t_{\text {общ }}-t_{\text {горячей воды }}\right)+c_{\text {воды }} * m_{\text {холодной воды }} * \left(t_{о б щ}-t_{\text {холодной воды }}\right)\] - Заменяем символы числами:
\[\begin{aligned}
&4200 * 0,2 *\left(t_{\text {общ }}-80\right)+4200 * 0,1 *\left(t_{\text {общ }}-15\right)=0 \\
&840 *\left(t_{\text {общ }}-80\right)+420 *\left(t_{\text {общ }}-15\right)=0
\end{aligned}\] - Раскрываем скобки и получаем ответ \[t_{\text {общ }}=58,33\]
Ответ: Температура смешанной воды будет равна 58,33 градуса Цельсия.
Пример на определение массы пара
В латунный калориметр, который имеет массу \[m_{k}=0.1\] килограмм со льдом, который имеет массу \[m_{i}=1\] килограмм , которые имеют общую температуру \[T_{k i}=200 \mathrm{~K}\], начали пускать пар, который имеет температуру \[T_{p}=400 \mathrm{~K}\]. После этого, в калориметре изменилась температура и стала постоянной \[\Theta=300 K\].
Вопрос:
Какую массу имел пар?
Примечание:
Считать, что система, состоящая из льда, колориметра и пара — изолирована. Следовательно, теплообмена с окружающей средой нет.
Решение:
Исходя из условия задачи, мы можем сделать вывод, что все процессы теплообмена, которые будут происходить в системе, можно описать с помощью уравнения теплового баланса, учитывая агрегатные превращения.
В результате того, что лед плавится при помощи пара, калориметр наполняется водой ( если делать выводы по температуре, которая установилась в калориметре \[\Theta=300 K=27\] градусов Цельсия). Происходит теплообмен сред: пар отдает свою теплоту, а калориметр со льдом её получают.
К исходным данным добавляем справочные:
- Удельная теплоемкость пара \[c_{p}=1,7 * 10^{3} \frac{\text { Дж }}{кгК}\]
- Удельная теплоемкость воды \[c_{v}=4,2 * 10^{3}\frac{\text{ Дж }}{кгК}\]
- Удельная теплоемкость льда \[c_{i}=2,1 * 10^{3} \frac{\text { Дж }}{кгK}\]
- Удельная теплоемкость латуни \[c_{k}=0,386 * 10^{3} \frac{ \text { Дж }}{кгК}\]
- Удельная теплотапарообразования воды \[r=2,1 * 10^{6} \frac{\text { Дж }}{кг}\]
- Удельная теплотапри плавлении льда \[\lambda=3,3 * 10^{5} \frac{\text { Дж }}{кг}\]
Чтобы решить данную задачу, мы должны описывать каждую стадию изменения внутренней энергии.
- Пар, когда отдает теплоту, начинает остывать от своей температуры \[T_{p}\] до конденсированной \[T_{k o n d}\], которая равняется 373 К.
- Пар будет конденсироваться при постоянной температуре
- Вода, которая была получена из пара будет остывать до температуры \[\Theta\].
- Как результат внутренняя энергия пара становится меньше \[\Delta U_{1}=Q_{o t d}=m_{p} c_{p}\left(T_{p}-T_{c o n d}\right)+m_{p} r+m_{p} c_{v}\left(T_{k o n d}-\Theta\right)\].
- Происходит нагревания льда благодаря тому, что он получает теплоту от пара и он от \[T_{k i}\] доходит до \[T_{\text {plav }}\] и равняется 273 K.
- Плавление льда
- Нагревание воды до температуры \[\Theta\].
- Как результат, внутренняя энергия льда будет увеличена.
\[\Delta U_{1}=Q_{\text {poluch }}=m_{i} c_{i}\left(T_{\text {plav }}-T_{k i}\right)+m_{i} \lambda+m_{i} c_{v}(\Theta-T_{\text {plav }})\] - Происходит теплообмен с калориметром и он нагревается до \[\Theta\].
Составляем уравнение теплового баланса:
\[\Delta U_{1}=\Delta U_{2}+\Delta U_{3}\]
Для описания всего процесса составим уравнение теплового баланса:
\[\begin{aligned}
&m_{p} c_{p}\left(T_{p}-T_{\text {cond }}\right)+m_{p} r+m_{p} c_{v}\left(T_{\text {kond }}-\Theta\right)= \\
&m_{i} c_{i}\left(T_{\text {plav }}-T_{k i}\right)+m_{i} \lambda+m_{i} c_{v}\left(\Theta-T_{\text {plav }}\right)+ \\
&m_{k} c_{k}\left(\Theta-T_{k i}\right)
\end{aligned}\]
\[m_{p}=\frac{m_{i} c_{i}\left(T_{p l a v}-T_{k i}\right)+m_{i} \lambda+m_{i} c_{V}\left(\Theta-T_{\text {plav }}\right) m_{k} c_{k}\left(\Theta-T_{k i}\right)}{c_{p}\left(T_{p}-T_{\text {cond }}\right)+r+c_{V}\left(T_{\text {kond }}-\Theta\right)}\]
Заменяем символы на цифры:
\[\begin{aligned}
&m_{p}= \\
&\frac{1 * 2,1 * 10^{3} *(273-200)+1 * 3,3 * 10^{5}+1 * 4,2 * 10^{3} *(300-273)+0.1 * 3,9 * 10^{3} *}{1.7 * 10^{3} *(400-373)+2,1 * 10^{6}+4,2 * 10^{3} *(373-300)} \\
&=\frac{9,8 * 10^{5}}{2.5 * 10^{6}}=0.392(кг)
\end{aligned}\]
Ответ: Масса пара будет равна примерно 392 грамма.














