Законы Кеплера
Иоганн Кеплер — известный немецкий астроном, который пытался всю свою сознательную жизнь доказать, что из себя представляет Солнечная система. Его интересовали орбиты небесных светил, по которым тела в космическом пространстве движутся вокруг Солнца, а также он исследовал зависимость периодов прохождения любых небесных тел вокруг Солнца. Открытые Кеплером законы, обеспечили ему известность и славу до наших дней.
В своей работе он использовал не только собственные наблюдения, но и знаменитого датского исследователя Тихо Браге, который накопил очень большой объем сведений о движении планет. Кеплер был его ассистентом и после смерти ученого получил доступ к бесценным материалам по исследованиям Тихо Браге.
Первооткрыватель, исследователь законов перемещения планет — древний ученый Птолемей, в центр Вселенной помещал Землю. Он считал, что все звезды и планеты по малым и большим орбитам перемещаются вокруг Земли. Открытые законы Птоломея не вызывали сомнения у астрономов, но и не подтверждались.
В середине 16 века Коперник впервые озвучил теорию о гелиоцентрических системах движения планет. Согласно утверждениям Коперника, планеты движутся не вокруг нашей планеты Земли, а вокруг общего светила — Солнца.
Затем Кеплер выдвинул три новых закона движения тел в космическом пространстве в Солнечной системе. Эти законы Иоганна Кеплера были установлены на основе анализа личных наблюдений и Тихо Браге. Они были опубликованы ученым в 1609 и 1619 г.
Первый Закон Кеплера
Закон: Орбиты тел в космосе, представляют из себя эллипсы. В одном из фокусов орбит располагается Солнце.
Этот закон посвящен описанию траекторий перемещения тел в космическом пространстве. У планет степень вытянутости орбит (эксцентриситеты) и их удаление от Солнца, происходит в ближайшей к нему точке (в перигели) и в самой удаленной точке (апогели) различные. При этом у всех эллиптических орбит одно общее — Солнце всегда находится в одном из двух фокусов эллиптической фигуры.
Первый Закон Кеплера проиллюстрирован на рисунке, на котором изображена планета. В одном из фокусов эллиптической траектории планет, находится Звезда. Между этими точками располагается ось эллипса.
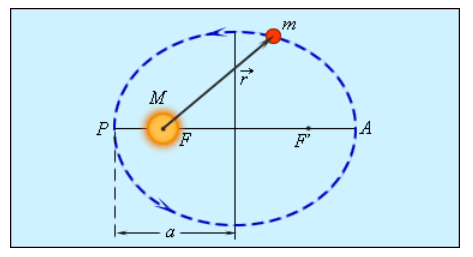
Историческое научное значение этого закона заключается в том, что до него астрономы считали, что планеты в космическом пространстве передвигаются всегда по круговым орбитам.
Второй закон Кеплера
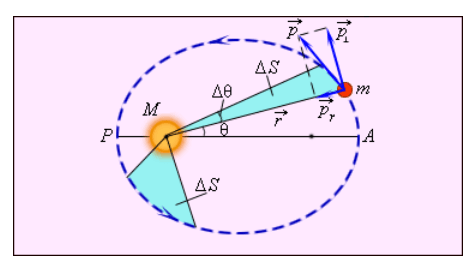
Закон площадей: Радиус-вектор, который можно прочертить между любой планетой и Солнцем, отсекает за равные временные интервалы и равные по площади сектора.
\[\Delta \mathrm{S}=\frac{1}{2} \mathrm{r}^{2} \Delta \theta \text { или } \frac{\Delta \mathrm{S}}{\Delta \mathrm{t}}=\frac{1}{2} \mathrm{r}^{2} \frac{\Delta \theta}{\Delta \mathrm{t}}=\frac{1}{2} \mathrm{r}^{2} \mathrm{w}, \text { где } \mathrm{w}- \text { угловая скорость. }\];
Он установил, что: чем ближе расположена планета к Солнцу, тем с большей скоростью происходит её движение в космическом пространстве. Также тем короче отрезки, которые соединяют на орбите два положения планеты с фокусом эллипса (в нем расположено Солнце). Подтверждает эмпирически этот закон, открытый ранее Закон сохранения импульса Ньютона.
Третий закон Кеплера
Закон: Квадраты периода обращения планет имеют такое же соотношение между собой, как и кубы полуосей орбит.
\[\mathrm{T}^{2} / \mathrm{a}^{3}=\text { const } \text { или} \mathrm{T}_{1}^{2} / \mathrm{a}_{1}{ }^{3}=\mathrm{T}_{2}{ }^{2} / \mathrm{a}_{2}{ }^{3}\]
Третий закон Кеплера даёт возможность уже производить сравнение орбит планет между собой. Согласно Закону Кеплера, чем дальше от Солнца размещена планета, тем больше времени при движении по орбите необходимо для совершения полного оборота (дольше «год» на планете). Сегодня известны два важных фактора — скорость перемещения планет снижается с увеличением расстояния планеты от Солнца и тем периметр её орбиты становится длиннее.
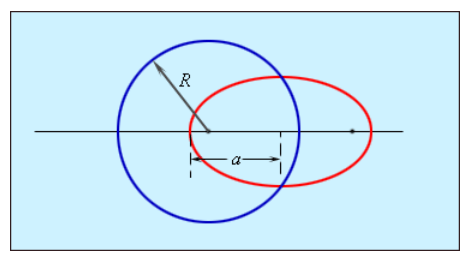
На рисунке проиллюстрированы две орбиты, по которым космические тела во Вселенной движутся вокруг других космических тел. Одна орбита имеет радиус R, а другая, в виде эллипса, имеет большую полуось а. При равенстве R и а, согласно этому Закону, периоды обращения тел в космическом пространстве по орбитам будут равными.
Законы Кеплера были получены на основе только наблюдений (эмпирически). Фундаментально, теоретически обосновывает Законы Кеплера, подтверждают их универсальность Законы Ньютона. Законы Кеплера с использованием математических вычислений могут быть выведены из Закона всемирного тяготения, Законов механики и Закона сохранения импульса Ньютона.
Ньютон был первым из исследователей, который установил, что в космосе между любыми телами действуют гравитационные силы, которые и определяют перемещение космических тел в пространстве. Частным случаем является только взаимодействие космических тел, расположенных на поверхностях и рядом с планетой — сила тяжести, она немного корректирует их движение.
Законы Кеплера можно применять к любой планетной системе Вселенной. Они применимы не только к движению планет, но и к передвижению космических кораблей и запущенных искусственных спутников Земли. Для них центром тяготения будет не Солнце, а Земля.
Астрономы, которые ищут планетные системы в мировом пространстве, используют до сих пор уравнения Кеплера для вычислений и исследования орбит удаленных и даже невидимых планет. Труды знаменитого ученого, который верно впервые описал устройство нашей Солнечной системы, спустя века, имеют большое значение в изучении Вселенной.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Гравитация
В космическом пространстве именно притяжение между объектами удерживает различные предметы и живые существа на поверхности планеты. Благодаря силе притяжения, вокруг звёзд удерживаются планеты, спутники продолжают движение по своим орбитам и не уходят в космическое пространство.
Сила притяжения зависит от массы, размеров объекта, который окружает гравитационного поле. Чем сильнее это поле, тем выше ускорение движения тела и больше его вес (например, сила притяжения и вес космонавта в 6 раз больше на Земле, чем на Луне).
Действие сил гравитации между объектами даже очень большого веса (в сотни и тысячи килограммов) определить довольно сложно. В микромире наблюдаются другие силы взаимодействия между атомами и элементарными частицами. Силы гравитации в нем очень невелики и их можно не учитывать в математических расчетах.
Закон притяжения
Притяжение небесных тел изучались многими учёными, но впервые научно были обоснованы, доказаны путём математических расчётов английским ученым в 17 веке Ньютоном. Он доказал прямую взаимосвязь между движением планет и тяготением. Открытия Ньютона были самыми популярными в науке более двух столетий до создания теории относительности.
Формула Закона притяжения имеет вид:
\[\mathrm{F}=\mathrm{G} \mathrm{M} \mathrm{m} / \mathrm{r}^{2}\]
где M и m – массы Солнца и планеты, r – расстояние между ними, а постоянная сила гравитации \[\mathrm{G}=6,67 \times 10^{-11} \mathrm{Hм}^{2} / \mathrm{кг}^{2}\]
Ньютон – первый исследователь, который сделал важнейший вывод, что именно от сил притяжения зависит характер движения тел во Вселенной.
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике