Таблицы истинности логических функций и их построение

Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.

Понятие таблиц истинности

Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.

Правила того, как следует проводить построение таблицы истинности

Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:

• Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2ⁿ;
• Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
• В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
• Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.

Порядок действий при построении таблицы истинности для логических выражений

Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:

1. Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
   X = n + m, Y = 2ⁿ+1.
   Где n – число переменных, m – чило логических операций.
2. Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
3. В первых столбцах перечислить всевозможные комбинации входных значений;
4. Выполняя заданные логические операции, заполнить все оставшиеся ячейки;

Ответом следует считать последний заполненный столбец таблицы.

О порядке логических операций

Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.

После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.

Далее приведём несколько поучительных задач на построение таблиц истинности

Задачи 1 — 3

Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B

Решение:

1. 1. Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
   2. Определяем, сколько будет у на строк. Оно равно 2ⁿ, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2ⁿ+1 = 2² + 1= 5;
   3. Заполняем первую строку. Прописываем символы переменные и логических операций;
   4. В двух первых столбцах записываем возможные значения переменных;
   5. В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
   6. В самом последнем из столбцов записываем итоговые значения функции.

В результате всего этого у нас должно получиться:

---

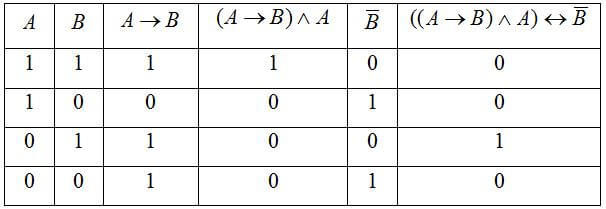
Провести построение таблицы истинности функции (A ∨ B) ∧ – C

Решение:

1. Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
2. Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 2³ + 1= 9;

3. Заполняем первую строку. Прописываем символы переменные и логических операций;
4. В два первые столбца вносим возможные значения наших переменных;
5. В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
6. В последнем столбце записываем итоговые значения функции.

В итоге получим таблицу:

---

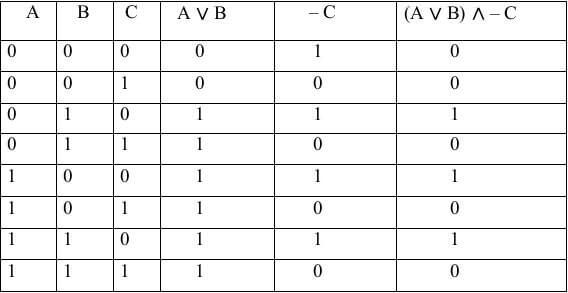
Сделать таблицу истинности для

(A ∧ B ↔ B ∧ C) ∨ (C → A)

Функция посложнее и таблица получится значительно больше, чем предыдущая.

1. Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
2. Считаем строки. Их количество будет 2³+1= 9;
3. Заполняем первую строку таблицы;
4. В первых столбцах записываем все допустимые значения наших переменных;
5. В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
6. В последний столбец пишем итоговые значения данной нам функции.

В итоге у нас получается таблица:

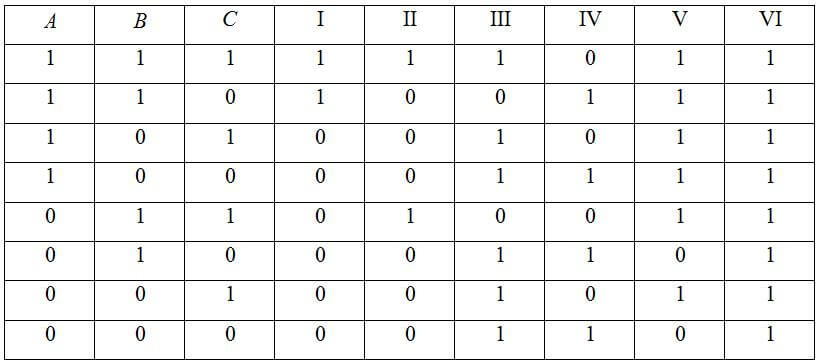
Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Построения функции, если известна её таблица истинности

Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.

Алгоритм действий для получения СДНФ по таблице истинности:

1. Отметьте в таблице строки, в которых значение функции равняется 1
2. Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
3. Все полученные конъюкции свяжите в дизъюкцию.

Аналогичным образом определяется СКНФ

В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.

Правило + задача

СДНФ всегда равно СКНФ. СДНФ = СКНФ.

Дана таблица истинности:

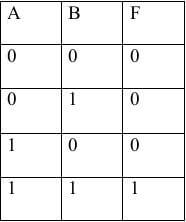
Выделяем в ней цветом строку

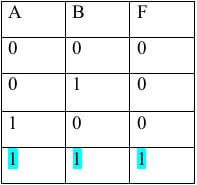
Заполняем столбцы с СДНФ и с СКНФ

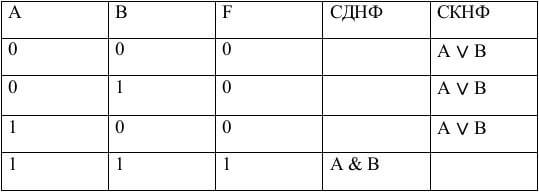
Записываем СДНФ

СДНФ = A & B

Записываем СКНФ

СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)