Деление натуральных чисел столбиком: правило, примеры
Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы. При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.
В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи чисел при делении столбиком
Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:
Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:
Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
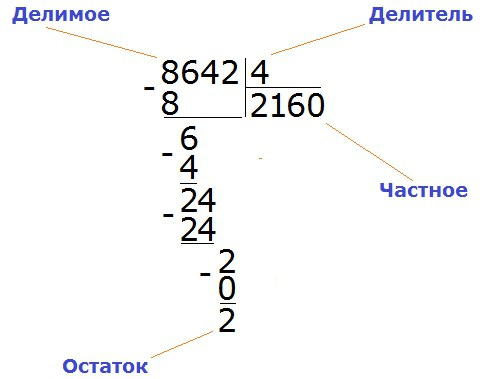
Из схемы выше видно, что частное будет написано под делителем, т.е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.
Деление столбиком на однозначное число
Практические навыки лучше всего отрабатываются на простых примерах. Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3. Итак, сначала запишем делимое и делитель по методу деления в столбик:
Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.
Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.
Итак, мы имеем число, равное делимому. Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:
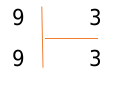
Теперь осталось вычесть числа под делителем (тоже методом столбца). В нашем случае 9 — 9 = 0.
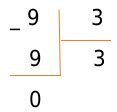
Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления. Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.
Разделим натуральное число 7 на натуральное число 5.
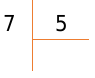
При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:
Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.
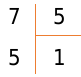
В завершение операции вычитаем 5 из 7 и получаем:
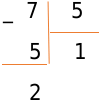
Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.
Изучим механизм деления столбиком на примере деления числа 140288 на число 4.
Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.
Алгоритм деления столбиком
Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.
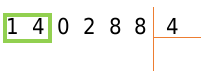
Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее. Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца. Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.
В соответствии с алгоритмом имеем:
Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.
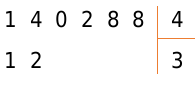
Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
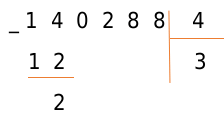
Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого. Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0. Соответственно, помечаем новое рабочее число — 20.
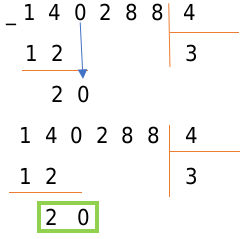
Важно
Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.
Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: \[4 \times 5=20\]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.
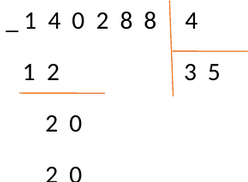
Проведем вычитание: 20 − 20 = 0
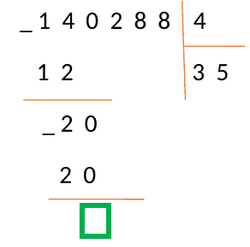
Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.
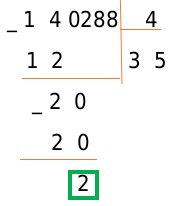
Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:
Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.
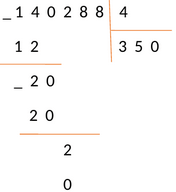
Выполняем операцию вычитания и записываем результат под чертой.
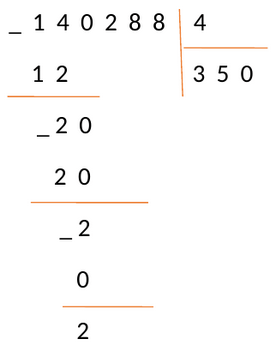
Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.
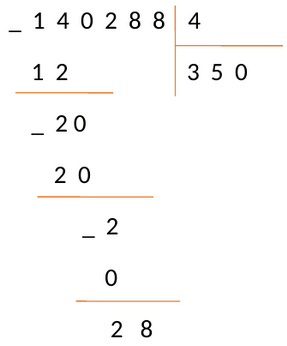
Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.
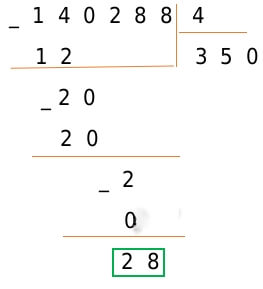
Вычислив все по правилам, получаем результат:
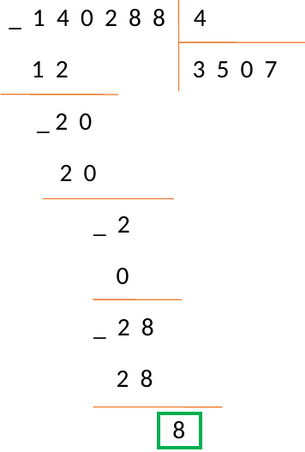
Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:
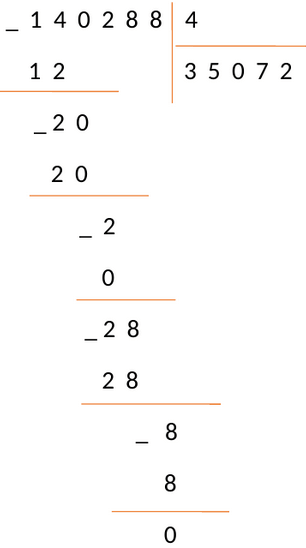
В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.
Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:
- Делим тысячи;
- Делим сотни:
- Делим десятки;
- Делим единицы.
Рассмотрим другие примеры:
Пример №1
Выполним деление 7485 на 3:
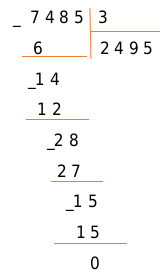
Следовательно, 7485 : 3 = 2495
Проверка:
2495*3=7485
Пример № 2:
Разделим 318624 на 6:
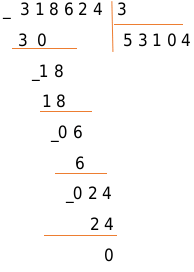
Проверка: \[54104 \times 6=318624\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Деление на многозначные натуральные числа столбиком
Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число. Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.
Пример №3
Разделим 5562 на 206.
В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:
Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.
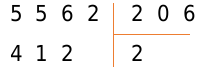
Продолжаем вычисления:
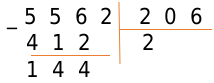
В результате получаем число 144. Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.
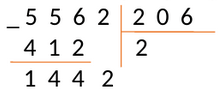
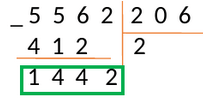
Повторяем пункты 2 − 4. Получаем:
Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
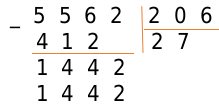
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
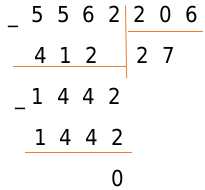
Ответ: 27
Пример № 4
Разделим 36261 на 153
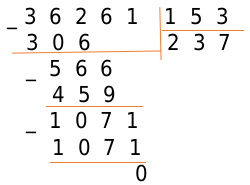
Проверка: \[237 \times 153=36261\].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
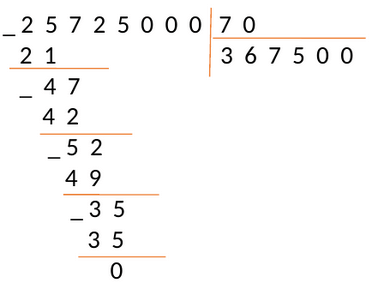
Проверка: \[367500 \times 70=25725000\].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
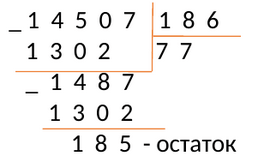
Проверка: \[186 \times 77=14507\].
Пример №7:
Разделим 300428 на 505
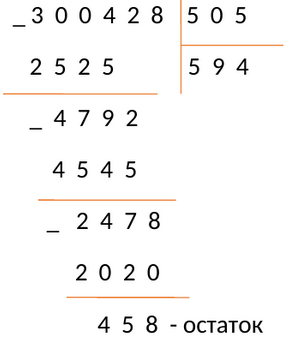
Проверка: \[505 \times 594=300428\].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: \[1505,86 \div 43=35,02\].

Пример №8:
Разделим 5612,8 на 350,8
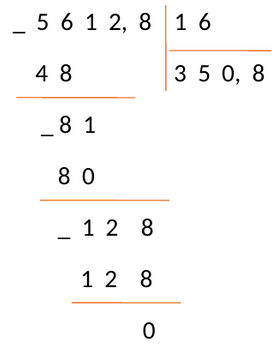
Проверка: \[350,8 \times 16=5612,8\]















