Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
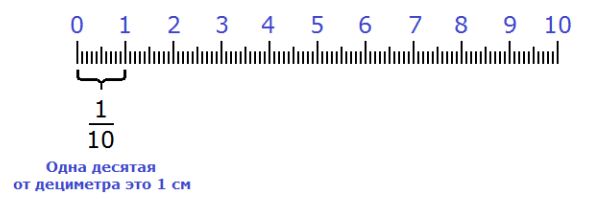
Часто бывает, что показать значение лучше в дробном выражении. К примеру, одну десятую часть дециметра можно представить так: \[\frac{1}{10} \text{дм}\].
Выражение обозначает, что дециметр разделили на 10 равных частей, и одна из этих частей была взята. В данном случае эта часть будет равна 1 сантиметру.
Если нужно показать в дробном виде 6 см и 3 мм в сантиметрах, представим выражение в виде десятичной дроби. Один миллиметр – это десятая часть сантиметра, соответственно 3 мм это три десятых, записываются так: \[\frac{3}{10} \mathrm{см}\].
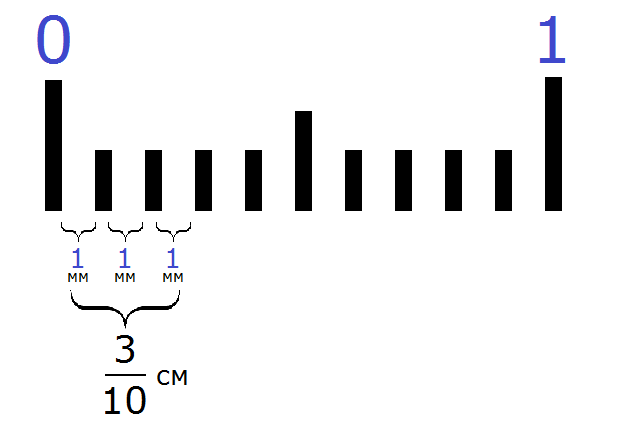
Выражение обозначает, что один сантиметр был разделен на 10 равных частей и взяли три из них. В результате получается: \[6 \frac{3}{10}см\].
Дробь можно прочитать как шесть целых три десятых сантиметра. Если знаменатель дроби представлен числами 10, 100, 1000 эту дробь можно записать без знаменателя в виде целой и дробной части без знаменателя. Целая и дробная часть между собой разделяются запятой, получается 6,3 см. Каждое число, записанное в таком виде, считается десятичной дробью.
Что такое десятичная дробь
Десятичные дроби представляют собой целые числовые выражения, в знаменатель которых десять в какой-либо степени.
Для чего нужны десятичные дроби
- удобнее сравнивать;
- сокращение вычислений;
- удобная запись в одну строчку.
Чтобы записать десятичную дробь выполняют следующие действия:
- Отдельно написать числитель.
- Передвинуть десятичную точку на количество нулей знаменателя.
- После того, как десятичная точка сдвинулась, зачеркните нули, которые остались в конце записи.
Если на втором шаге недостаточно цифр для завершения действия, на недостающих позициях проставляются нули. Примеры десятичной записи.
В знаменателе первой дроби стоит 10, значит, числитель первой дроби 73 сдвинем на один знак. Получается 7,3.
Знаменатель второй дроби 100, а числитель 9. Сдвигаем десятичный знак на два знака и получаем 0,09.
Знаменатель третьей дроби 1000, а числитель 10029. Сдвигаем десятичную точку на три знака и получаем 10,029.
В последней дроби числитель 10500, перемещаем точку на три знака 10,500. Образовавшиеся в конце записи нули убираем, и получаем ответ 10,5.
Два последних примера показывают, как правильно поступать с нулями. Если нули получились справа в конце – их следует зачеркнуть, а если в середине, как в третьем примере, то их оставляем. Это цифры внутри числа.
Конечные десятичные дроби
Конечные десятичные дроби – это вид десятичной дроби, в которых содержится конечное число знаков после запятой. Например: 0,367; 3,7. Каждую из этих дробей можно записать как смешанном числом либо обыкновенной дроби.
Приведем пример, конечную десятичную дробь 5,63 легко представить как \[5 \frac{63}{100}\], десятичную дробь 0,2 можно привести к виду \[\frac{2}{10}\].
Обратные процесс записи обыкновенной дроби в десятичном виде выполняется не в каждом случае. Например, дробь \[\frac{5}{13}\] заменить, на аналогичную дробь со знаменателем 100, 10 нельзя.
Класс периодических и непериодических дробей
Если в десятичной дроби после запятой стоит бесконечное количество цифр, такие дроби называют бесконечными.
Такие дроби целиком записать невозможно, следовательно, при записи указывается лишь часть из них, далее записывается многоточие. Это обозначает бесконечную последовательность знаков после запятой. Примеры класса бесконечных десятичных дробей: 0,143346732…; 3,1415989032…; 2,6666666666…
После запятой могут стоять периодичные повторения одного знака или группы знаков.
Периодические дроби – это бесконечные десятичные дроби, в которых после запятой стоят повторяющиеся группы цифр или повторяется одна цифра.
Например, для десятичной дроби 3,444444… периодом будет 4, для 76,134134134134… периодом будет группа чисел 134.
Чтобы записать представить запись десятичной периодичной бесконечной дроби в сокращенном виде, достаточно указать период одни раз в скобках. Так для 3,444444… запись выглядит так 3,(4), дробь 76,134134134134… можно представить в виде 76,(134). Смысл остается тем же самым. Такую запись используют, чтобы избежать ошибок. В скобки заключают максимально короткую последовательность цифр, которые расположены ближе всего к запятой.
Каждую конечную дробь можно выразить как периодическую. В таком случае, добавляют бесконечное множество нулей в правой части выражения. Например, конечная дробь 45,32 в периодическом виде записывается как 45,32(0). Таким образом, добавление нулей в правую часть десятичной дроби дает равную ей дробь.
Бесконечные десятичные периодические дроби являются рациональными числами. Любую десятичную можно записать в виде обыкновенной и наоборот.
Дроби, у которых нет бесконечной последовательности после запятой, называют непериодическими. Внешне они бывают похожими на периодические, с записями наподобие 9,03003000300003… нужно быть внимательно, знаки после запятой одинаковые, но не повторяются. Такие дроби являются иррациональными и в обыкновенные дроби их не переводят.
Арифметические действия с десятичными дробями
Теоретические и практические уроки предполагают следующие действия с десятичными дробями, их можно: складывать, вычитать, умножать делить, сравнивать между собой.
Правила действий с десятичными дробями
- Сделать одинаковым число знаков после запятой.
- Выполнить запись в столбик друг под другом, запятая должна быть под запятой.
- Выполнить сложение (вычитание).
Действия с десятичными дробями: сложение
Действия удобнее выполнять в столбик. Целые и дробные части складывают по отдельности. Например, выполним сложение дробей 3,2 и 5,3. Для этого запишем две дроби в столбик, при этом целые части следует записать под целыми, а дробные под дробными (запятая под запятой).
В первую очередь складываем дробные части и записываем пятерку под чертой. Далее складываем целые части, пишем восьмерку в целой части ответа. Дробную часть от целой отделяем запятой. Получаем ответ 8,5.
Пример правильной записи:
Пример неправильной записи:
Место расположения цифр в десятичной дроби влияет на значение в десятичной дроби. Разряды, расположенные до запятой, носят названия аналогичные натуральным числам, после запятой первая цифра обозначает разряд десятых, вторая – сотых, третья – тысячных.
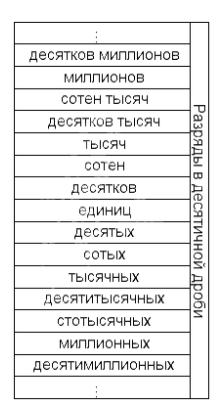
Разряды различаются по старшинству, если рассматривать цифры слева на право, то будем двигаться от старших разрядов к младшим.
В качестве примера возьмем десятичную дробь 0,345
Позиция тройки находится в разряде десятых.
Позиция четверки – в разряде сотых.
Пятерки – тысячных.
Расположение тройки в разряде десятых сообщает о том, что в рассматриваемой дроби 0,345 содержится три десятых \[\frac{3}{10}\]; четыре сотых \[\frac{4}{100}\]; пять десятитысячных \[\frac{5}{1000}\]. При сложении дробей получим изначальную.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Сложение десятичных дробей
Правила сложения десятичных дробей те же, аналогичные сложению обычных чисел. Сложение выполняется согласно разрядам: десятки с десятками, сотые с сотыми. Соблюдение правила «запятая под запятой» обеспечит этот порядок. Сложение начинают с крайнего правого ряда и двигаются влево к предыдущему.
Математические действия с десятичными дробями:
- для сложения периодических десятичных дробей следует их заменить обыкновенными;
- бесконечные непериодические дроби складывают, предварительно округлив до некоторого разряда, чем меньше разряд, тем выше точность;
- для сложения десятичной дроби и натурального числа, натуральное число складывают с целой частью десятичной дроби, а дробную оставляют неизменной.
Вычитание десятичных дробей
Для выполнения вычитания соблюдаются правила, идентичные сложению: запятая под запятой и одинаковое количество цифр после запятой.
Найти значение разности 2,5 — 2,2
Записываем выражение, соблюдая правило запятой и вычисляем дробную часть 5-2=3. Далее выполняем действие с
целой частью 2-2=0. Получаем следующую запись:
\[\begin{array}{r}-\begin{array}{r}2,5\\2,2\\\end{array} \\\hline\begin{array}{r}0,3\end{array}\end{array}\]
Ответ: 2,5-2,2=0,3
Действия с десятичными дробями: примеры
Вычислить 7,353-3,1
Для решения выражения, нужно сделать равным количество цифр в дробях. Для этого следует добавить два нуля в
дроби 3,1. Записываем выражение в столбик:
\[\begin{array}{r}-\begin{array}{r}7,353\\3,100\\\end{array}
\\\hline\begin{array}{r}4,253\end{array}\end{array}\]
Ответ: 4,253
При выполнении вычитания десятичных дробей, в отдельных случаях придется занимать единицу, как и в обычных числах.
Умножение десятичных дробей производится аналогично натуральным числам. Метод вычисление столбиком тоже подходит. Выполняя действие, на запятые можно не обращать внимание. Вычислив ответ, нужно отделить дробную часть от целой. Для этого в обеих дробях подчитайте количество цифр после запятой. В ответе подсчитываем столько же цифр и ставим запятую.
Вычислить 2,5х1,5
Перемножаем дроби, не обращая внимания на запятые.
\[\begin{array}{r}*\begin{array}{r}25\\15\\\end{array}
\\\hline+\begin{array}{r}125\\25\\\hline\begin{array}{r}375\end{array}\end{array}\end{array}\]
\[\begin{array}{r}*\begin{array}{r}2,5\\1,5\\\end{array} \\\hline\begin{array}{r}3,75\end{array}\end{array}\]
Запятая сдвигается на два знака, с учетом того, что в первой дроби один знак и во второй один знак.
Ответ: 3,75
Деление десятичной дроби на натуральное число производят по правилам деления в столбик. при выполнении действия на запятую не обращают внимания. В полученном частном запятая проставляется, когда заканчивается целая часть делимого. В случае, когда целая часть делимого меньше делителя, тогда в частном будет 0 целых.
Сравнение десятичных дробей
При сравнении двух дробей, большей будет та, у которой больше целая часть.
7,99>6,399
Если целые части дробей одинаковы, большей будет та, у которой больше десятых. Если равны десятые, то больше сотые и т.д.
85,7>85,679















