Сумма разрядных слагаемых натурального числа
Для того, чтобы выполнить некоторые действия над натуральными числами необходимо представить эти числа в виде суммы разрядных составляющих или, как говорят, разложить натуральные числа на цифры. Не менее важен и обратный процесс, который заключается в записи натурального числа в виде суммы разрядных составляющих.
Как найти натуральное число, если известна его подобная сумма?
Для того, чтобы проделывать некоторые действия, нужно представлять начальные выражения в виде сложенных чисел – другим языком, необходимо разложить числа по разрядам. Противоположный процесс также безгранично важен при решении задач и упражнений.
Разрядные слагаемые – это такие числа, которые состоят исключительно из нулей и единственной цифры, отличной от нуля. Такие натуральные числа, как 5, 20, 400, 100, принадлежат данной категории, а числа 55, 213, 680, 324, 458, 25, 694, 25 и другие – не относятся.
Число разрядных слагаемых у некоторого числа равно тому числу, сколько цифр содержатся в записи. Представление числа 61 в виде суммы разрядных слагаемых, станет выглядеть как 6 и 1, они отличаются от 0. Когда есть необходимость разложить 55050 как сумму слагаемых разрядов, оно будет представлено в виде трех слагаемых. Три пятерки, что присутствуют в записи, отличны от нуля.
Необходимо помнить, что каждое разрядное слагаемое содержит отличное от других количество знаков в собственной записи.
Сумма разрядных слагаемых числа, принадлежащего к классу натуральных, обязательно эквивалентна данному числу.
Натуральные числа, в записи которых присутствует цифра, что отлична от нуля, называются разрядными слагаемыми.
Количество чисел обязано быть равно количеству тех цифр, которые не равных нулю. Каждое слагаемое может быть записано с разным количеством знаков. Если необходимо разложить по разрядам, то при сложении получившихся цифр, мы получим число равно данному числу.
При анализе понятия, можно сформулировать вывод, что многозначные и однозначные числа, которые полностью состоят из нулей за исключением первой цифры, нельзя представлять в виде суммы. Это происходит в том случае, когда такие числа сами будут разрядными слагаемыми для каких-то чисел.
Исключая данные числа, все остальные примеры могут раскладываться на слагаемые.
Правила разложения чисел
Чтобы разложить число на сумму разрядных слагаемых, необходимо вспомнить, что каждое натуральное число связано с количеством определенных элементов. При записи числа разложение зависит от числа единиц, десятков, сотен, тысяч и т.д. К примеру, если взять число 937, то можно увидеть, что ему соответствует 9 сотен, 3 десятка и 7 единиц. Число 245 500 соответствует 2 сотням тысяч, 4 десяткам тысяч, 5 тысячам и 5 сотням. Эти числа можно представить в виде равенств — 900 + 30 + 8 = 938 и 245 500 = 200 000 + 40 000 + 5 000 + 500. В данных примерах можно наглядно увидеть, как число можно разделить на сумму цифр. Рассматривая этот пример, мы можем представить всевозможное натуральное число в виде суммы его разрядных членов. Вот еще один пример. Представим натуральное число 724 как сумму составляющих цифр. 724 равно 7 сотням, 2 десяткам и 4 единицам, поэтому 724 = 700 + 20 + 4. Однако сумма 312 + 412 не является суммой составляющих цифр числа 724, потому что нельзя иметь два числа, которые состоят из одинакового количества цифр. Мы уже рассматривали ключевое понятие. Разрядные слагаемые названы так потому, что они принадлежат к конкретному разряду.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры задач
Пример 1. Известна сумма разрядов, как же найти само число?
Чтобы решить этот пример, давайте рассмотрим обратную задачу. Представим, что мы знаем сумму слагаемых цифр. Нам нужно найти заданное натуральное число.
Например, сумма 300 + 40 + 9 равна 349, а сумма 30 000 + 3 000 + 600 + 20 + 7 соответствует натуральному числу 33627. Поэтому легко определить натуральное, если вы знаете сумму его вспомогательных слагаемых.
Другой способ найти натуральное — сложить столбцы сумм цифр. Этот пример не должен вызвать у вас затруднений. Рассмотрим его более подробно.
Пример 2. Нужно найти исходное число, когда дана сумма разрядных концов 300 000 + 50 000 + 2000+ 400 + 40 + 7.
Далее приступим к решению. Необходимо записать числа 300 000, 50 000, 2000, 400, 40, 7 сложить в столбик: осталось лишь сложить все числа в столбик. Важно помнить о том, что сумма нулей равна нулю и что сумма нулей и натурального числа равна натуральному числу.
Таким образом, выполнив сумму, мы получаем натуральное — 352447, сумма цифр которого равна 300 000 + 50 000 + 2000 + 400 + 40 + 7.
Поговорим еще об одном методе. Если мы научились делить числа и преобразовывать их в виде суммы понятий с цифрами, мы также можем представлять данные числа в виде некоторой суммы без цифр.
Пример 3. Разложение числа 5825 представляется как 49565 = 40000 + 9000 + 500 + 60 + 5, а сумма разрядных компонентов 5000 + 800 + 20 + 5 может быть представлена как (40000 + 9000) + (500 + 60) + 5 = 49565 или (40000 + 9000 + 500 + 60) + 5 = 49565 или 40000 + (9000 + 500 + 60) + 5 = 49565 и многие другие способы. Иногда сложные расчеты можно немного упростить. Приведем еще один небольшой пример для наилучшего закрепления представленной информации.
Пример 4. Вычтите числа 67838 и 780. Сначала представим — 67838 как сумму разрядных компонентов: 67838 = 60000 + 7000 + 800 + 30 + 8. Выполнив операцию, можно сделать вывод, что сумма (60000+7000)+ (800 + 30 + 8) = 67000 + 838. Тогда 67838 — 780 = (67000 + 838) — 780 = 67000 + (838 — 780) = 67000 + 58 = 67058.
Стоит рассмотреть обратную задачу более подробно. Считайте, что у нас есть сумма разрядных составляющих натурального числа, и нам нужно найти это число.
Например, сумма 300+20+9 является разложением разрядных чисел 329, а сумма разрядных слагаемых вида 3 000 000 + 40 000 + 4 000 + 500 соответствует натуральному числу 3 044 500.
То есть 600 + 20 + 9 = 629, а 3 000 000 + 30 000 + 4 000 + 500 = 3 034 500.
Чтобы найти положительное число по известной сумме разрядных слагаемых, можно сложить эти разрядные слагаемые в столбик (при необходимости обратитесь к материалу по сложению целых положительных чисел в столбик). Рассмотрим решение этого примера.
Найдите целое положительное, если сумма разрядных составляющих равна 200 000 + 40 000 + 50 + 5.
Запишите числа 200 000, 40 000, 50 и 5 так, как того требует метод сложения в столбик:
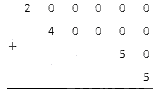
Осталось только сложить все эти числа в столбик:
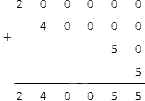
Под горизонтальной чертой мы получили искомое натуральное число.
В заключение мы хотели бы обратить ваше внимание еще на один момент. Умение раскладывать натуральные числа на цифры и умение выполнять обратное действие позволяет представить натуральное в виде суммы слагаемых, которые не являются разрядными.
Например, разрядное сложение целых положительных чисел 643 имеет следующий вид 643 = 600 + 40 + 3, а сумма разрядных слагаемых 700 + 20 + 5 в силу свойств сложения целых положительных чисел может быть представлена как (600 + 40) + 5 = 640 + 3 или 600+(40 + 3) = 600 + 43, или (600 + 3) + 40 = 603 + 40.
Возникает логичный вопрос: «Для чего это нужно? Ответ на него прост: в некоторых случаях это может упростить вычисления.
Пример 4. Вычтем целые положительные числа 5 799 и 790.
Сначала представим вычитаемое как сумму разрядных компонентов: 5 799 = 5 000 + 700 + 90 + 9.
Легко увидеть, что сумма разрядных компонентов равна сумме (5000 + 9) + (700 + 90) = 5009 + 790.
Тогда 5 799 — 790 = (5 009 + 790) — 790 = 5 009 + (790 — 790) =5 009 + 0=5 009.















