Умножение десятичных дробей
Данный материал будет посвящен изучению дробных чисел. А именно десятичных дробей их основных свойств и правил умножения.
Мы рассмотрим все виды дробей и как с ними работать. Какие способы применяют для их быстрого и точного вычисления
Для начала дадим определение десятичной дроби. Это число, которое после запятой имеет характерный остаток
Примеры десятичных дробей: 145,14; 12,85; 1,23.
В свою очередь данный вид дробей подразделяется на следующие категории:
- Конечные — если после запятой присутствует окончательное число.
Например: \[\pm a_{0} a_{1} a_{2} a_{3} \ldots . . a_{n}\]
- Бесконечные — количество цифр после запятой, не имеют окончательного значения, то есть они бесконечны.
Например: \[\pm a_{0} a_{1} a_{2} a_{3}\]
Основные свойства дробей:
Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.
Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.
Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей
- 0,900 = 0,9;
- 22,10200000 = 22,102;
- 0,45000=0,45;
- 0,12569000=0,12569;
- 0,780=0,78.
Основные характеристики десятичных дробей
- Дробное число, не будет иметь какого — либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
- Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — нет.
- Если значения, которые находятся в числителе и знаменателе разделить или умножить на любое действительное число. То получится дробь равная ей по значении.
- Если взять две дроби: \[\frac{a}{b} \text { и } \frac{c}{d}\] то они называться будут равными при \[a \cdot d \text { или } b \cdot c\].
Существующая взаимосвязь между дробями различных категорий и видов
- Целая часть десятичной дроби всегда будет равной такой части дроби, только смешанного типа;
- Когда значение в числителе меньше значения знаменателя, то нулю равна целая часть дроби;
- Количество значений после запятой, определяется в зависимости от количества нулей, которые записаны в знаменателе обыкновенной дроби.
Правило записи десятичной дроби
Пример №1. Нужно преобразовать обыкновенную дробь \[\frac{16}{10}\] в десятичную.
Принцип решения задачи:
Если в знаменателе число 10, а по правилам это будет только один ноль. Справа налево отсчитываем, в числителе один знак. И после этого ставим запятую. Получаем десятичную дробь, где: число один является целой частью, а шесть дробной.
\[\frac{16}{10}=1,6\]
Пример №2: Перевести \[\frac{39}{1000}\] в десятичную дробь.
Теперь видим, что, знаменатель равен 1000 и нужно использовать для решения три нуля. Проводим те же действия что и в первом примере. Получаем десятичную дробь. Где нулевое значение — это целая часть, а все остальное — это дробная часть.
\[\frac{39}{1000}=0,039\]
Ознакомившись кратко с десятичными дробями, перейдем к изучению правил их умножения.
Принцип умножения десятичных дробей
Для умножения десятичных дробей необходимо, произвести следующие действия.
- Дробь записать в виде так называемого математического столбика. Далее рассмотреть заданное значение, как обыкновенные действительные числа и подсчитать их;
- Все знаки за запятой подсчитать и сложить сумму;
- Полученную сумму справа налево отложить и поставить запятую.
Для данного вида дробей характерны все те же действия, что и для остальных чисел.
Если переставить местами множители, на окончательный ответ это не повлияет.
если мы хотим умножить число на произведение двух и более. Сначала умножаем данное число на первый множитель затем полученное значение на второй и так далее.
Чтобы умножить сумму на множитель. Нужно по отдельности умножить числа и полученную сумму сложить.
Если проводим умножение на разность чисел, то для начала умножаем на уменьшаемое, а затем на вычитаемое. Следовательно полученные значения вычитаем.
Также процесс умножения можно упростить. Десятичные дроби умножить как действительные целые числа, и поставить запятую.
Для наглядности рассмотрим несколько примеров:
Пример №1:
Определить произведение чисел \[1,5 \cdot 0,75\]
Первым делом преобразуем дробь. Заменим десятичную. на обыкновенную.
0,75=75/100
\[1,5=\frac{15}{10}\]
Затем проводим сокращение дробных значений и выделяем, по уже изученным правилам целую часть.
\[\frac{125}{1000}\] можно преобразовать и получить следующую дробь 1,125.
Ответ: 1,125.
Пример №2:
Определить произведение чисел \[5,382 \ldots \cdot 0,2\]
Первое значение является бесконечной дробью. Ее рекомендуется округлить до сотых значений. Получается \[5,382 \ldots \approx 5,38\].
Второй множитель округлять не требуется, это не имеет смысла.
Далее можно произвести вычисление \[5,38 \cdot 0,2=\frac{538}{100} \cdot \frac{2}{10}=\frac{1,076}{1000}=1,076\]
Следовательно, получаем ответ к нашей задаче: 1,076.
Пример №3:
Необходимо умножить две периодические дроби.
\[0,(3) \cdot 2,(36)\]
Преобразуем заданные значения в обыкновенную дробь.
Полученную в конечном итоге обыкновенную дробь приводим к десятичной. В столбик разделим числитель на знаменатель.
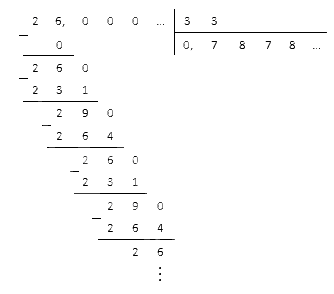
Окончательный ответ : \[0,(3) \cdot 2,(36)=0,(78)\].
Умножение десятичных дробей при помощи столбика
Умножение столбиком выполняя на условии, что на запятые никакого внимания не уделяется (они игнорируются)
В итоговом результате ставится знак запятой справа. Отделяется столько запятых, сколько множители имеют десятичных знаков вместе.
Если не хватает цифр, то принято в окончательном ответе дописывать нули.
Рассмотрим примеры решения подобных задач.
Пример №1:
Нужно найти значение произведения, следующих чисел: 63,37 и 0,12.
Выполняем умножение, не обращая внимание на запятые.
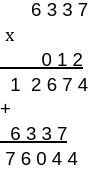
Далее определяемся с запятой, где ее ставить. Она будет через четыре цифры справа. Потому что сумма десятичных знаков двух множителей равна 4.
Нули в данной ситуации не записываются. Это связано с достаточным количеством чисел.
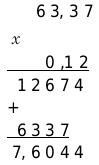
Получаем окончательное значение равное 7,6044.
Пример №2:
Заданные числовые, дробные выражения 3,2601 и 0,0254, необходимо умножить между собой.
Для этого применим умножение столбиком.

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны. Потому что заданные дроби, вместе, имеют восемь знаков после запятой.
Нули в данной ситуации записываются. Это связано с недостаточным количеством значений.
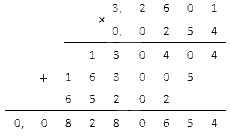
Получаем окончательное значение равное: 0 , 08280654
Как правильно умножить десятичные дроби на 0,001;0,01;0,1.
Для того чтобы умножить десятичную дробь на следующие значения: 0,1;0,01; 0,001, необходимо перенести знак запятой. Переносится знак в левую сторону, на количество знаков равное количеству нулей перед единицей.
Значение ноль целых, так же отсчитывается. При нехватке количества цифр, нужно дописать недостающее количество нулей.
\[35,9 \cdot 0,1=3,59;\]
\[1,9 \cdot 0,1=0,19;\]
\[145,6 \cdot 0,01=1,456;\]
\[9644,1 \cdot 0,001=9,6441;\]
\[22,9 \cdot 0,0001=0,00229.\]
Решим несколько примеров для закрепления материала.
Нужно произвести умножение значение: 9,4 и 0,0001.
Так как 0,0001 имеет четыре нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.
\[9,4 \cdot 0,0001=0,00094\]
Ответ: 0,00094.
Нужно произвести умножение значение: 11.4 и 0,001.
Так как 0,001 имеет три нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.
\[11,4 \cdot 0,001=0,00114\]
Ответ: 0,00114.
Умножаем следующие значения: 6,4 и 0,01.
Так как 0,01 имеет два нуля, то переносим запятую в первом множителе заданное количество и получаем следующее значение.
\[6,4 \cdot 0,01=0,064\]
Ответ: 0,064.
Условие умножения десятичной дроби с натуральным показателем
Принцип умножения дробей данного вида, такой же как и между десятичными. Используются и принимаются к сведению все те правила, которые были изучены ранее.
Подробно рассмотрим на примерах и решим их.
Пример №1:
Нам нужно вычислить произведение из числовых значений.
\[15 \cdot 2,27\]
Для этого воспользуемся правилом умножения через столбик.
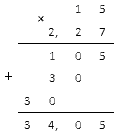
Следовательно, ответ задачи, исходя из вычисления равен: 34,05.
Пример №2:
Даны числовые значения 0,(42) и 22. Необходимо найти их произведение.
Для начала преобразуем периодическую дробь в обычную.
И получим следующее выражение:
\[0,(42)=0,42+0,0042+0,000042+\ldots=\frac{0,42}{1-0,1}=\frac{0,42}{0,99}=\frac{42}{99}=\frac{14}{33}\]
Следом проводим умножение: \[0,(42) \cdot 22=\frac{14}{33} \cdot 22=\frac{14 \cdot 22}{3}=\frac{28}{3}=9 \frac{1}{3}\].
Итоговый результат, будет записываться в виде периодической дроби, как и было задано изначально.
Ответ: \[0,(42) \cdot 22=9,(3)\]
Пример №3:
Даны значения и нужно их умножить \[(4 \cdot 2,145)\]
Для начала округляем бесконечную дробь до сотых значений. Умножаем полученные значения и получаем окончательный ответ к задаче.
\[4 \cdot 2,145 \ldots \approx 4 \cdot 2,15=8,60\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как умножить десятичную дробь на 1000, 100, 10
Чтобы выполнить умножение на перечисленные числовые значения, нужно вспомнить правило переноса запятой. Это перенос вправо на количество нулей в множителе. Имеющиеся лишние нули можно просто убрать. А при недостатке нулевых значений, их можно дописать.
\[1,11 \cdot 10=11,1\]
\[22,335 \cdot 100=2233,5\]
\[8,79 \cdot 1000=8790\]
\[0,34678 \cdot 10000=3467,8\]
\[0,02 \cdot 1000=20\]
\[0,00045 \cdot 100=0,045\]
Разберем на числовом примере принцип решения подобных задач:
Пример №1:
Вычислить значения 100 и 0,0783
Сначала переносим в десятичной дроби знак запятой. Так как в значении 100 два нуля, то запятая вправо переносится на два значения.
Следовательно, мы получаем следующее значение 007,83. Первые два нуля убираем, за ненадобностью и получаем ответ 7,83.
Ответ: \[0,0783 \cdot 100=7,83\]
Пример №2:
В этой задаче нужно найти значение двух числовых данных 0,2 и 10 000.
Вправо переносим запятую на четыре цифры. Так как второй множитель имеет четыре нуля. Так как нулей в исходном значении недостаточно их нужно дописать. Нам необходим только один ноль. Из этого получаем следующее число 0,02000. Переносим знак запятой вправо и получаем 0200,0. Передний ноль перед двойкой убираем. Он нам не нужен. И получаем следующий ответ задачи: 200.
Принцип умножения десятичной дроби с обыкновенной и со смешанной дробью
Чтобы произвести данную операцию, необходимо выполнить следующие требования:
- Десятичную дробь преобразовывают в обыкновенную и умножаем с нужным числом.
- В десятичную переводим обыкновенную или смешанную дробь и далее умножаем друг с другом.
Ниже приведены примеры решения задач.
Пример №1. Найти произведение \[\frac{3}{5}\] на 0,9.
Поэтапный процесс решения.
1) Записываем 0,9 в виде обыкновенной дроби, а именно \[0,9=\frac{9}{10}\]
2) Умножаем цифры по правилам математики \[\frac{3}{5} \cdot \frac{9}{10}=\frac{27}{50}=0,54\].
Ответ: \[\frac{3}{5} \cdot 0,9=0,54\]
Пример №2. Найти произведение чисел \[0,18 \text { на } 3 \frac{1}{4}\].
Выполняем следующие действия:
1) Записываем \[3 \frac{1}{4}\] в виде десятичной дроби: \[3 \frac{1}{4}=3,25\].
2) Вычисляем известные нам значения: \[0,18 \cdot 3,25=0,585\]
Ответ: \[0,18 \cdot 3 \frac{1}{4}=0,585\]
Пример №3:
Даны следующие значения \[0,4 \text { и } 3 \frac{3}{5}\]. По условию задач нужно найти их произведение, иными словами умножить.
Первым делом 0,4 переведем в десятичную дробь и получим значение: \[0,4=\frac{4}{10}=\frac{2}{5}\].
Затем проводим вычисление: \[0,4 \cdot 3 \frac{3}{5}=\frac{2}{5} \cdot \frac{23}{6}=\frac{23}{15}=1 \frac{8}{15}\].
Полученный ответ является смешанным значением. Его необходимо перевести в значение периодической дроби. А именно: 1,5(3).
Следовательно, это и ответ задачи. 1,5(3).
Пример №4:
Вычислить произведение заданных чисел: \[3,5678 \ldots . . \text { и } \frac{2}{3}\]
Второй множитель, можно рассмотреть и записать как \[\frac{2}{3}=0,666 \ldots \ldots\]
Затем оба множителя распишем, и получим тысячный разряд. Получаем десятичные дроби и вычисляем значения. 3,568 и 0,667.
Для расчета применяем расчет с помощью столбика.

Получим итоговый результат и округлим его до трех знаков после запятой. Потому что именно до тысячных знаков, мы округляем исходные данные.
\[2,379856 \approx 2,380\]
Тема десятичных дробей материал довольно емкий. Который включает в себя много различных моментов. Их необходимо учитывать при решении задач и примеров. А именно:
- принцип переноса знака запятой, на количество нулей;
- преобразование десятичных дробей в иной вид дроби.
Обязательно помнить один из главных моментов в алгебре, а именно деление на ноль. Точнее сказать его запрет. Всегда нужно, помнить, что на ноль деление запрещается. И если нулевое значение имеет числитель дроби, то она всегда будет приравнена к нулю.
Соблюдая все изученные характеристики и свойства дробей, а также главные правила математики, можно решать задачи данного типа без особых трудностей.















