Умножение натуральных чисел столбиком: примеры, решения
Умножение натуральных чисел в столбик – это способ, который позволит перемножить без калькулятора любые многозначные числа. Чтобы пользоваться таким методом на практике, нужно знать правила его применения. Рассмотрим подробнее умножение разных чисел в теории и на примерах.
Основные закономерности умножения столбиком
Есть ряд математических правил, которые нужно помнить, чтобы успешно пользоваться таким методом умножения:
- Во-первых, нужно знать наизусть таблицу умножения, и, не задумываясь использовать ее.
- Во-вторых, не стоит забывать правила умножения на нуль. Нуль часто встречается в двух и трехзначных числах, а значит, будет выступать в качестве одного из множителей.
- Помним, что \[x \times 0=0\]
- Под x мы понимаем любое натуральное число.
- Прежде, чем решать примеры на умножение в столбик, стоит вспомнить правила сложения в столбик и потренироваться суммировать числа.
- Повторить понятие разряда и сравнения любых натуральных цифр.
Как записывать множители при решении примеров на умножение столбиком
Залогом правильного решения задачи будет умение правильно записывать выражение столбиком. Здесь придерживаемся следующих правил:
- В качестве первого множителя записывается цифру, которая имеет больший разряд.
- Во второй строке (под первым множителем) записывается второй множитель. Здесь важно строго соблюдать закономерность сопоставления разрядов. Это значит, что десятки пишутся под десятками, единицы под единицами, и никак иначе.
- Записав все множители друг под другом, нужно подвести горизонтальную черту, которая отделит их от ответа.
Рассмотрим на примере, как записать такое выражение.
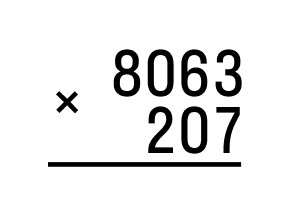
На примере мы видим, как соблюдаются разряды при умножении четырехзначной цифры на трехзначную.
Теперь, чтобы научиться умножать в столбик, потребуется разобраться, как происходит умножение и как записывается результат. Начнем с умножения многозначного множителя на однозначный.
Как происходит умножение двузначных чисел в столбик на однозначные
Если требуется решить пример на умножение многозначного натурального числа на однозначное, легко можем применить данный метод. Процесс решения сразу рассмотрим ниже.
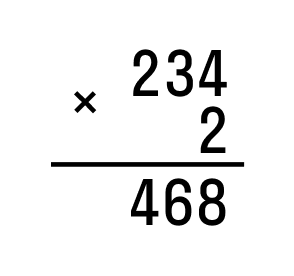
Разберем алгоритм действий:
- Записываем множители в столбик, строго соблюдая разряды. Единицы пишем под единицами, следовательно, 2 под 4.
- Перемножаем их по порядку, так же соблюдая разряд. Сначала перемножаем на 2 единицы, потом десятки, потом сотни. Полученный результат вписываем под чертой.
Здесь стоит отметить, что в образце приведены числа, при перемножении которых результат не превысил 10. В том случае, если при перемножении мы получаем двузначный ответ, то записываем только единицы. Десятки запоминаем и прибавляем к результату, который получится при перемножении следующего разряда. Если количество разрядов закончилось, а остались неучтенные десятки, они просто вписываются крайней левой цифрой.
Умножение в столбик с нулями
Если нам потребуется решить пример по математике, где один из множителей имеет на конце нули, действовать придется несколько иначе. Рассмотрим на конкретном примере.
Условие: нам нужно умножить 5400 на 7.
Первым делом нужно правильно записать выражение:
Здесь нужно обратить внимание на то, что под нулями множитель не записывается.
Следующий этап решения примера в столбик – умножение без учета нулей.
Теперь вспоминаем, что у нас осталось два неучтенных нуля. Их просто переносим вниз за черту.
В итоге получаем: 5400×7=37800

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как умножать столбиком, если в примере два многозначных числа
Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения. Предположим, нам нужно умножить 8063 на 207.
Решение:
- Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
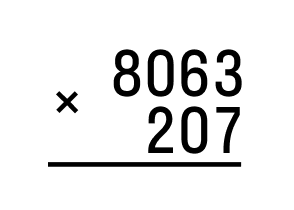
- Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
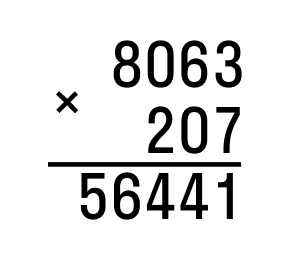
- Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
- Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат. Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
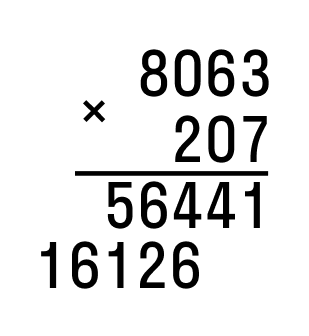
В итоге мы получили два неполных произведения. Задания на умножение столбиком содержат столько промежуточных результатов, сколько разрядов во втором множителе. У нас получилось два, так как в десятках мы имеем нуль, и его пропускаем. Если бы вместо него была любая другая натуральная цифра, мы бы записали три неполных произведения друг под другом со сдвигом влево. - Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.
Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.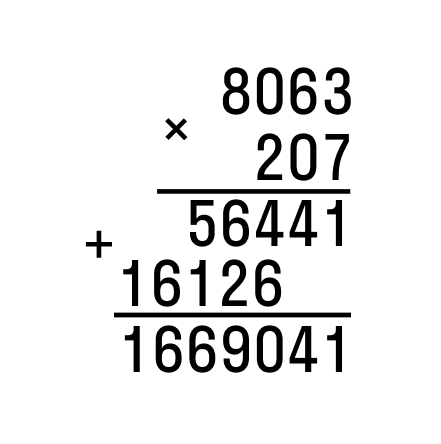
Таким образом, можно записать выражение:
8063×207=1669041
Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.
Под основными терминами понимаются следующие:
- Однозначное число – это число, состоящее из одной цифры (например, 6).
- Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
- Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
- Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.
Например, число 4657.
7 – разряд единиц;
5 – разряд десятков;
6 – разряд сотен;
4 – разряд тысяч.
Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.
Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.
- Перестановка мест множителей не влияет на результат.
\[x \times y=y \times x\] - Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.
\[x \times y \times z=(x \times y) \times z\] - Умножение на нуль всегда дает нуль.
Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули. В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.
Пример умножения чисел столбиком
Условие: 34500×230
Первым делом нужно записать пример в столбик таким образом, чтобы натуральные числа, отличные от нуля, расположились друг под другом.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\end{array}\]
После того, как мы записали пример в столбик, мы можем просто перемножить множители в соответствие с
правилами перемножения многозначных чисел, без учета нулей.
В ходе вычислений у нас должно получиться два неполных, или промежуточных результата.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline\end{array}\]
Последний этап – сложение двух промежуточных результатов и переписывание справа нулей. Нулей мы напишем столько, сколько имеют оба множителя, а именно, три.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array} \\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline7935000\end{array}\]
В итоге получаем, что 34 500×230=7 935 000
Анализируя вышеперечисленный пример, можно сказать, что перемножить в столбик можно любые без исключения числа, если руководствоваться правилами математики. Умножение двузначных чисел в столбик – это школьная программа, освоив которую, примеры научится решать любой ребенок, ученик четвертого класса.















