Умножение обыкновенных дробей: правила, примеры, решения
В статье мы рассмотрим правила умножения обыкновенных дробей, умножения их на натуральные числа и перемножения между собой трех и более обыкновенных дробей.
Как умножать обыкновенные дроби между собой
Для начала ознакомимся с основным правилом: при умножении двух обыкновенных дробей числители каждой из них перемножаются друг на друга, то же самое производится со знаменателями. Это можно представить в следующем виде: \[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\].
Применим вышеуказанную формулу для вычисления площади. Предложим, что имеется некий квадрат со стороной равной единице, его площадь соответственно тоже равна 1 кв. единице. Разделим квадрат на равные прямоугольники со стороной \[\frac{1}{8}\] и \[ \frac{1}{6}\] от единицы. Всего у нас получится \[8 \cdot 6=48\] прямоугольников. Легко подсчитать, что площадь каждого будет равняться \[\frac{1}{48}\] кв. единицы. Затем выделяем некую часть внутри фигуры.
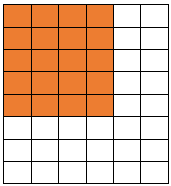
Мы получили заштрихованный фрагмент со сторонами, равными \[\frac{4}{6}\] и \[ \frac{5}{8}\] от числовой единицы. Результат произведения двух этих дробей будет являться площадью заштрихованного участка. Однако мы можем просто сосчитать количество таких клеток, их 20, следовательно площадь фигуры составит \[\frac{20}{48}\] кв. единиц.
Так как \[5 \cdot 4=20 \text { и } 8 \cdot 6=48\], мы позволим себе записать следующее равенство: \[\frac{4}{6} \cdot \frac{5}{8}=\frac{20}{48}\].
Решение подтверждает ранее сформулированное правило умножения, которое выглядит как \[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\]. Оно применимо для правильных и неправильных дробей, с его помощью перемножаются дроби с разными и одинаковыми знаменателями.
Пройденную тему стоит закрепить, поэтому далее разберем решение нескольких примеров.
Пример 1
Умножьте \[\frac{6}{7} \text{ на } \frac{8}{9}\].
Решение
Умножаем числители дробей, помножив 6 на 8. У нас получилось \[6 \cdot 8=48\]. Произведение знаменателей вычислим схожим образом \[7 \cdot 9=63\]. Запишем ответ из двух получившихся чисел \[\frac{48}{63}\].
Полное решение можно записать следующим образом:
Ответ: \[\frac{6}{7} \cdot \frac{8}{9}=\frac{48}{63}\].
Если ответ подлежит сокращению, то нужно выполнить это действие, если полученная дробь — неправильная, то стоит выделить из нее целую часть.
Пример 2
Подсчитайте произведение \[\frac{6}{10} \text { и } \frac{45}{8}\].
Решение
Выше мы ознакомились с первым правилом перемножения дробей, применим этот способ и запишем решение в таком виде:
Полученная дробь является сократимой и имеет признаки делимости на 10.
Сократим полученную дробь: \[\frac{270}{80}\] НОД (270,80) = 10, \[\frac{270}{80}=\frac{270: 10}{80: 10}=\frac{27}{8}\]. В результате дробь получилась неправильной, поэтому выделим целочисленное значение и получим смешанное число: \[\frac{27}{8}=3 \frac{3}{8}\].
Ответ: \[\frac{6}{10} \cdot \frac{45}{8}=3 \frac{3}{8}\].
Для удобства подсчета исходные значения можно привести к виду \[\frac{a \cdot c}{b \cdot d}\]. После чего переменные нужно разложить на простые множители, затем сократить одинаковые числа. Для этого запишем следующий пример.
Пример 3
Подсчитайте произведение \[\frac{6}{10} \cdot \frac{45}{8}\].
Решение
Запишем решение в соответствии с правилами умножения:
Представим числители и знаменатели как: \[6=3 \cdot 2,45=5 \cdot 9, 10=5 \cdot 2,8=4 \cdot 2\] следовательно \[\frac{6.45}{10.8}=\frac{3.2 .5 .9}{5.2 .4 .2}\].
Сокращаем некоторые множители:
Осталось лишь перемножить числа и выделить целое число из неправильной дроби:
Существует определенное правило, как умножать обыкновенные дроби, используя переместительное свойство. При необходимости порядок расстановки множителей можно изменить:
Умножение обыкновенных дробей на натуральное число
Для умножения обыкновенной дроби на натуральное число достаточно умножить числитель на данное число, оставив знаменатель без изменения.
Произведение дроби \[\frac{a}{c}\] и натурального числа n можно записать как формулу \[\frac{a}{c} \cdot n=\frac{a \cdot n}{c}\].
Любое натуральное число можно представить в виде обыкновенной дроби, в математике умножение обыкновенных дробей на натуральное число можно представить следующим образом:
Поясним как умножить обыкновенную дробь на натуральное число на конкретных примерах.
Пример 4
Произведите умножение \[\frac{3}{20}\] на 5.
Решение
Выполним такое действие как умножение числителя обыкновенной дроби на целое натуральное число и получим 15. Учитывая вышеназванное правило, получим \[\frac{15}{20}\]. Запишем полное решение:
Ответ: \[\frac{3}{20} \cdot 5=\frac{3}{4}\].
Такое действие как умножение обыкновенных дробей на натуральные числа, часто приводит к сокращению решения или представлению его в виде смешанного числа.
Пример 5
Найдите решение произведения 7 на \[\frac{12}{10}\].
Решение
Учитывая прошлый пример, перемножаем натуральное число на числитель — \[\frac{12}{10} \cdot 7=\frac{12 \cdot 7}{10}=\frac{84}{10}\]. Найденные два числа являются четными, поэтому нужно провести сокращение.
НОК (84,10) = 2, следовательно, \[\frac{84}{10}=\frac{84: 2}{10: 2}=\frac{42}{5}\].
Остается выделить целую часть и получить ответ: \[\frac{42}{5}=8 \frac{2}{5}\].
Итоговое решение можно представить в следующем виде: \[\frac{12}{10} \cdot 7=\frac{12 \cdot 7}{10}=\frac{84}{10}=\frac{42}{5}=8 \frac{2}{5}\].
Подобное решение можно было бы найти при помощи разложения числителя и знаменателя на простые множители, ответ остался бы без изменений.
Ответ: \[\frac{12}{10} \cdot 7=8 \frac{2}{5}\].
Подобные выражения так же обладают свойством перемещения, поэтому порядок размещения множителей не влияет на результат:

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Произведение трех и более обыкновенных дробей в одном выражении
Переместительное и сочетательное свойства позволяют перемножать между собой неограниченное количество дробей. Мы можем умножать обыкновенные дроби как обычные натуральные числа. Приведем еще два примера. Не стоит использовать калькулятор для данного урока, поскольку такие примеры легко исчисляются в тетради.
Пример 6
Найдите произведение четырех дробей \[\frac{1}{8}, \frac{3}{10}, \frac{12}{7} H \frac{4}{9}\].
Решение
Сделаем необходимую запись произведения \[\frac{1}{8} \cdot \frac{3}{10} \cdot \frac{12}{7} \cdot \frac{4}{9}=\frac{1 \cdot 3 \cdot 12 \cdot 4}{8 \cdot 10 \cdot 7 \cdot 9}\].
Разложим некоторые множители, это позволит упростить задачу, нежели затем сокращать готовую дробь.
Ответ: \[\frac{1 \cdot 3 \cdot 12 \cdot 4}{8 \cdot 10 \cdot 7 \cdot 9}=\frac{2}{70}\].
Пример 7
Произведите действия умножения со следующими числами \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10\].
Решение
Для удобства сгруппируем числа \[\frac{5}{6} \text { и } 6, 8 \text{ и } \frac{3}{40}\], поскольку их можно легко сократить. В итоге получим: \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10=\left(\frac{5}{6} \cdot 6\right) \cdot\left(\frac{3}{40} \cdot 8\right) \cdot 10=\frac{5 \cdot 6}{6} \cdot \frac{3 \cdot 8}{40} \cdot 10=\frac{5}{1} \cdot \frac{3 \cdot(4 \cdot 2)}{(4 \cdot 2) \cdot 5} \cdot 10=5 \cdot \frac{3}{5} \cdot 10=\frac{150}{5}=30\]. В последней части используем деление числителя на знаменатель и получаем целочисленный результат.
Ответ: \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10=30\].
Перевод смешанных дробей в неправильные
Когда числитель больше либо равен знаменателю, такие дроби принято называть неправильными. Существует правило, согласно которому из неправильной дроби нужно выделить целую часть и только тогда записывать ответ на задание. Достаточно разделить числитель на знаменатель, записав полученное целочисленное значение перед дробью, остаток поместить в числитель, а знаменатель оставить без изменений.
Обратное же действие требует умножить целочисленную часть на знаменатель, прибавить к полученному значению числитель. Итоговое число станет новым числителем, знаменатель останется без изменения. Рассмотрим на конкретном примере. Подобные темы проходятся обычно в младших классах.
Пример 8
Переведите смешанную дробь \[3 \frac{3}{5}\] в неправильную.
Решение
Согласно вышеназванному правилу, умножим знаменатель 5 на целое число 3, прибавив текущий числитель 3, получим следующее выражение:
Ответ: \[3 \frac{3}{5}=\frac{18}{5}\].















