Разложение чисел на простые множители
Разложение натурального числа на простые множители
Перед тем как приступить к рассмотрению принципа разложения чисел, сформулируем определение простого множителя числа.
Простое число — это целое число больше 1, единственные делители которого равны 1 и
самому себе.
Фактор значения
— это целое число, которое можно равномерно разделить на другое число.
Первые несколько простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29. Числа, содержащие более двух множителей, называются составными числами. Число 1 не простое и не составное.
Простые числа могут использоваться по ряду причин. Например, некоторые типы криптографии будут использовать простые числа. Для каждого простого числа, например: «p», существует простое число, которое больше p, называемое p ‘. Это математическое доказательство, которое было продемонстрировано в древние времена греческим математиком Евклидом, подтверждает идею о том, что не существует «наибольшего» простого числа. По мере того, как набор натуральных чисел N = {1, 2, 3, …} продолжается, простые числа, как правило, становятся менее частыми, и их значение труднее найти.
Простой множитель — это числовое значение, которое представлено в виде простого числа.
Если, рассмотреть составное число, то можно сделать вывод, что его можно преобразовать и представить в виде простых чисел.
Рассмотрим пример разложения чисел:
При разложении числа могут повторяться, как в третьем примере. Чтобы исключить повтор, их лучше всего скомпоновать и представить в виде степени.
Пример: 24 = 2 · 2 · 2 · 3 = 23 · 3.
Рассмотрим другой пример разложения числа на множители. Возьмем число 609840 и распишем его на составные множители.
Запишем следующее выражение: \[609840=2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 11 \], преобразуем его в канонический вид и получим пример: \[609840=2^{4} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 11^{2}\].
Применяя каноническое уравнение, можно определить значение всех делителей и их количество.
Основные свойства простых чисел:
Существует несколько свойств простых чисел. Большая часть из них считается доказанной, остальную часть, так и оставили недоказанной.
Среди доказанных свойств, можно выделить следующие:
- Множество простых числовых значений, является бесконечным. Иными словами, простые числа не имеют наибольшего значения.
- Если значение p – минимальный простой делитель числа n. Из этого следует доказательство, p2 ≤ n.
В случае, если p — делитель составного числа n, тогда должен быть другой делитель q, для числового значения n.
Значение n, должно быть представлено, как произведение числовых множителей p и q.
Делителей меньше значения p не должно быть, так как данный множитель является наименьшим простым делителем. Из данного условия составим неравенство:
\[q \geq p . \Rightarrow p \cdot p \leq p \cdot q, \text { т. e. } p 2 \leq p q \text { или } p 2 \leq n .\]
Данное свойство, принято использовать для проверки на простой множитель.
Если есть простой делитель любого составного числа, и квадрат числа является меньшим или равен ему. В этом случае не требуется определять другие делители. Для того чтобы доказать, что проверяемое значение является простым.
Достаточно будет провести проверку на делимость значения n на простые делители p \[\Rightarrow\]p2 ≤ n.
Из данного значения n нужно извлечь корень и обязательно округлить его до целого числа. Затем нужно перебрать все делители до числа, полученного при вычислении. Если не один из них не подходит, значит простых делителей не существует, следовательно, проверяемое число — простое.
Пример:
Проверим число 37. Вычислим квадратный корень этого числа и округлим до целого значения. \[\sqrt{37} \approx 6\]
Далее нужно проверить значения на признак делимости, а именно на 2,3,4,5,6. После проверки, делаем вывод, что ни одно из значений 37 не делится. Из этого следует, что данное значение является простым.
Натуральные значения, выражаются в виде суммы из двадцати слагаемых.
«Теорема Ферма» Когда число p является простым и значение n на него нельзя разделить\[\Rightarrow\]np — 1 — 1 всегда делится на p.
Пример:
Число 34 нельзя разделить на 3. Однако 343-1 — 1 = 342 — 1 = 1156 — 1 = 1155\[\Rightarrow\]делится на 3.
Недоказанные свойства простых чисел:
- Любое из четного значения, можно представить в виде суммы двух и более простых чисел. Например: 18=10+8, 65=11+54, 108=70+38.
- Каждое максимальное значение нечетного числа, возможно расписать в виде суммы трех и более простых чисел.
- Максимальные значения простых чисел, можно выразить как сумма четырех нечетных значений.
- Четное значение можно расписать как разность двух и более простых значений.
Составим алгоритм, для разложения на простые множители чисел:
Последовательность действий при разложении числа на простые множители:
Чтобы разложить число на простые множители нужно знать несколько основных правил и действий.
- Число, которое нужно расписать на множители, нужно проверить по таблице простых чисел. А именно, определить не является ли оно простым.
- В случае, если число не является простым, пользуемся таблицей и подбираем самое наименьшее значение. Оно должно равняться числу, на которое можно поделить значение. Деление должно быть без остатка.
- Далее проверяем, по этой же таблице, простых чисел, полученное значение. Оно не должно быть простым.
- Если условие соблюдается, то поочередно подбираем наименьшее значение из таблицы. При делении на данное значение, вычисленное частное должно делиться без дробного остатка.
- Повторяем последние два пункта до тех пор, пока окончательный ответ, не будет равняться единичному значению.
Решим несколько примеров:
Пример №1:
Согласно задания нужно разложить на простые множители число 102.
Решение примера начнем с поиска минимального делителя для значения 102. Для этого нужно воспользоваться таблицей чисел простых значений. Затем последовательно определяем самое малое значение из таблицы, при делении на которое, ответ получится без дробного остатка.
Подбираем значение 2 и проводим деление заданного значения 102 на него и получаем выражение:
102:2 = 51.
Если число 102 разделить на 2, то получим ответ равный без остатка. Из этого следует, что два, является первым определенным простым множителем.
Следующим действием, будем проводить проверку частного простого числа. Значение 51, является составным числом. Берем наименьший делитель, равный двум. Но число 51, без остатка на два не делится. Поэтому переходим к следующему пункту алгоритма.
Берем следующее значение по таблице простых чисел — это 3. Проводим вычисление и получаем следующее выражение:
51:3 = 17
После вычисления примера получаем целое значение, без остатка. И это означает, что число три, является вторым множителем. Поэтому, можно сделать вывод, что число 51 записывается в виде произведения из трех множителей.
102 = 2 · 51 = 2 · 3 · 17
Проводим проверку значения, не является ли оно простым числом. Значение 17 — простое. Поэтому минимальным числом, на которое оно будет делится будет именно само числовое значение 17.
17:17 = 1
Так как полученный ответ равен единичному значению, то разложение на множители считается завершенным.
Запишем окончательное решение: 102 = 2 · 3 · 17.
В математике существует еще один вариант разложения на множители. Весь алгоритм решения записывается в виде столбика. Для этого применяются две колонки, которые разделены прямой линией.
Этот способ имеет следующий алгоритм решения:
сверху вниз, с левой стороны от вертикальной черты записывается заданное число;
затем записываем полученные частные значения;
по правую сторону от линии, нужно записать минимальные значения простых делителей.
Пример №2:
Записываем заданное число 120 и проводим по правую сторону вертикальную линию.
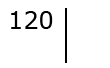
С правой стороны записывается простой делитель, наименьшего значения:
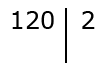
Проводим вычисление: делим число 120 на делитель 2 и получаем частное равное 60. Вычисленное значение нужно записать под числом 120 с левой стороны от вертикальной прямой.
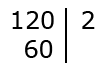
Определяем делитель наименьшего значения. Далее записываем его с правой стороны от черты под предыдущим делителем и вычисляем значение.
Вычисления нужно производит до тех пор, пока ответ не будет равен единице.
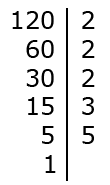
Разложение будет окончено, только тогда, когда окончательный ответ получится равным единичному значению.
Окончательный ответ записывается в строку:
120 = 23 · 3 · 5.
Примеры разложения чисел на простые множители
При решении задач данного типа, всегда нужно помнить и придерживаться основного алгоритма решения.
Пример №1:
Число 78 разложить на простые множители.
Для начала пересматриваем все простые числа, входящие в состав числа 78.
Берем число 2 и проводим вычисление: \[78 \div 2=39\].
Так как ответ при вычислении получается без остатка, то это значит, что значение 2 будет первым простым делителем. Дадим ему обозначение \[p_{1}\].
Запишем выражение следующего вида: \[a_{1}=a \div p_{1}=78 \div 2=39\]
Из этого следует следующее равенство \[a=p_{1} \cdot a_{1}\]. Подставим значения в уравнение: \[78=2 \cdot 39\].
Находим простой делитель \[p_{2}\] числа \[a_{1}\], которое равняется 39.
Перебираем все простые числа: \[39\div2=19\]. Деление получается с остатком, поэтому число два, не будет являться простым делителем. Далее берем число три: \[39\div3=13\].
Следовательно \[p_{2}\] будет являться наименьшим простым делителем для числа 39.
Запишем равенство: \[a=p_{1} \cdot p_{2} \cdot a_{2}=2 \cdot 3 \cdot 13=78\].Получаем следующее значение \[a_{2}=13\], оно естественно не равняется единице. Поэтому нужно проводить расчет далее, согласно алгоритму.
Применяем снова перебор чисел. Он необходим для, того чтобы найти наименьший делитель числа 13. Берем значение три и подставляем в пример: \[13\div3=4\] (остаток равен 1). Из решения видно,что 13 нельзя разделить на назначения 5,7,11, так как \[13\div5=2\] (остаток 3), \[13\div7=1\]
(остаток равный 6) и \[13 \div 11=1\] (остаток 2). Проведя все решения, можно сделать вывод, что число 13 равняется простым.
Продолжим решение и запишем следующую формулу:
Так как ответ равен единице, значит решение окончено. И множители будут записаны в следующем выражении: \[78=2 \cdot 3 \cdot 13\]


Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример №2:
Для решения возьмем число 86006 и разлом его множители. Разложим на простые множители значение \[p_{1}=2\]
Для проверки берем значения 2,3,5 и предполагаем, что они не простые числа.
\[a_{1}=41503 \Rightarrow 7 \] простой делитель, так как \[ 41503\div 7=5929. \]
Произведя расчеты получаем следующие действия: \[p_{2}=7 . a_{2}=a_{1} \div p_{2}=41503 \div 7=5929\]
Значение 83006 можно разложить на следующие множители \[2 \cdot 7 \cdot 5929\]
Определяем простой делитель наименьшего значения для \[a_{3}=847 \Rightarrow 7\].
\[a_{4}=a_{3} \div p_{4}=847 \div 7=121\], из этого следует, что \[83006=2 \cdot 7 \cdot 7 \cdot 7 \cdot 121\]
Числовое значение 11 будем применять, для определения делителя \[a_{4}=121 \Rightarrow p_{5}=11\].
Получаем следующее выражение: \[a_{5}=11 \text { значение } p_{6}=11\] и будет являться наименьшим простым делителем.
Следовательно: \[a_{6}=a_{5} p_{6}=11 \div 11=1 \Rightarrow a_{6}=1\]
Окончательный ответ в решении равен единице. Это означает окончание расчета.
И множители числа будут записаны в следующем выражении:
Преобразуем уравнение, так как имеются одинаковые множители, в каноническое.
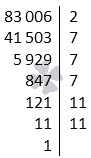
Пример №3:
Нужно разложить на составные множители число 897 924 289.
Решение начинаем с разбора простых множителей. Свой расчет начинаем со значения 2. Окончание перебора множителей будет число 937.
Отсюда следует, что: \[p_{1}=937 a_{1}=a \div p_{1}=897924289 \div 937=958297\] и \[ 897924289=937 \cdot 958297 .\]
Далее перебираем наименьшие простые числа. Для начала берем число 937. Так как 967 является простым делителем, его можно считать простым числом.
Значение 991 не имеет не одного простого делителя, поэтому, оно будет также являться простым числом.
Запишем подкоренное выражение \[\sqrt{991}\] и определим его примерное значение. \[\sqrt{991}<40^{2}\].
Из решения, можно сделать вывод, что \[p_{3}=991 \text { и } a_{3}=a_{2} \div p_{3}=991 \div 991=1\].
Расчет согласно алгоритма завершен, поскольку ответ равен один.
Записываем окончательный ответ к задаче: \[897924289=937 \cdot 967 \cdot 991\]
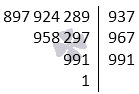
Применение при решении задач, признаков делимости для разложения на множители
При разложении чисел на множители, всегда необходимо использовать алгоритмы решения. Однако имеются случаи, когда разложить нужно число небольшого значения. Для этого можно применять обычные таблицы умножения или делимости.
Разберем несколько примеров:
Нужно разложить на простые множители число со значением равным 10. Применяем таблицу умножения и записываем, что \[2 \cdot 5=10\]. Числа 2 и 5 являются простыми значениями. Поэтому их можно назвать и простыми множителями для 10.
Рассмотрим еще одно значение равное 48. Снова воспользуемся таблицей перемножения данных. Запишем выражение: \[48=6 \cdot 8\].
Данные значения, не является простыми множителя, потому что их можно разложить: \[6=2\cdot3 \] и \[8=2\cdot4\]. Правильное разложение будет выглядеть следующим образом: \[48=6 \cdot 8=2 \cdot 3 \cdot 2 \cdot 4 \text {. }\]
Преобразуем уравнение и запишем его канонический вид: \[48=2^{4} \cdot 3\]
Для разложения значения 3400, нужно воспользоваться признаком делимости числа. Для данного значения это 10 и 100. Распишем число: \[3400=34 \cdot 100\], отсюда можно выполнить следующее действие 100 разделить на 10 и записать, что \[100=10 \cdot 10 \Rightarrow 3400=34 \cdot 10 \cdot 10 .\] Применяя основные признаки делимости значений, получаем выражение: \[3400=34 \cdot 10 \cdot 10=2 \cdot 17 \cdot 2 \cdot 5 \cdot 2 \cdot 5 .\]
Все числа относятся к простым множителям. Запишем выражение в виде канонического разложения.















