Функции y=|x|, y=[x], y={x}, y=sign(x) и их графики: основные концепции и практическое применение

Функции являются важным инструментом в математике и ее приложениях. Они позволяют описывать зависимость между величинами и решать различные задачи. В данной статье мы рассмотрим четыре важные математические функции: y = |x|, y = [x], y = {x} и y = sign(x), а также их графики.

Функция y = |x| представляет собой модуль числа x и имеет много интересных свойств. Функция y = [x] обозначает наибольшее целое число, не превышающее x, а функция y = {x} обозначает дробную часть числа x. Функция y = sign(x) возвращает знак числа x: 1, если x положительное, -1, если x отрицательное и 0, если x равно нулю.

В данной статье мы рассмотрим каждую из этих функций более подробно, описав их свойства, построив графики и рассмотрев примеры их применения в решении задач. Также мы проанализируем сходства и различия между функциями и рассмотрим их применение в различных областях науки и техники.

Функция y = |x|

Функция y = |x| является одной из самых простых и изучаемых функций в математике. Она описывает расстояние от числа x до нуля на числовой оси. Функция y = |x| может быть определена следующим образом:

y = |x| = {
x, x ≥ 0;
-x, x < 0 }

Свойства функции y = |x|: Функция является четной, то есть y = |x| = | -x |. Это означает, что график функции симметричен относительно оси y. Значение функции всегда неотрицательно или равно нулю. Функция имеет точку перегиба в точке (0, 0).

Построение графика функции y = |x|:

График функции y = |x| представляет собой положительную ветвь параболы, отраженную от оси x на отрицательную ветвь.

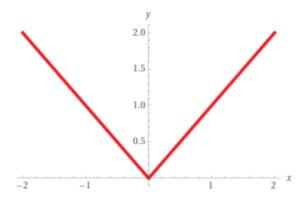
Примеры применения функции y = |x|: Решение уравнений, содержащих модуль числа. Вычисление расстояния между точками на плоскости. Использование в физических задачах для определения модуля вектора. В следующих разделах мы рассмотрим другие функции и их графики.

Функция y = [x]

Функция y = [x] обозначает наибольшее целое число, не превышающее x. Например, [3,14] = 3, [-2,5] = -3. Функция y = [x] может быть определена следующим образом:

y = [x] = max{k ∈ ℤ | k ≤ x}

Свойства функции y = [x]:

Функция является ступенчатой и постоянна на интервалах между целыми числами.
Функция не является непрерывной и не дифференцируемой на множестве действительных чисел.

Построение графика функции y = [x]:
График функции y = [x] представляет собой последовательность горизонтальных линий на уровне каждого целого числа.

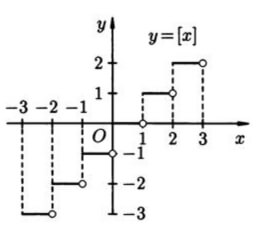
Примеры применения функции y = [x]:

Использование в комбинаторике для определения числа возможных вариантов перестановок и сочетаний.
Вычисление суммы целых чисел от 1 до n: 1 + 2 + … + n = [n(n+1)]/2.

В следующих разделах мы рассмотрим еще две функции и их графики.

Функция y = {x}

Функция y = {x} обозначает дробную часть числа x, то есть разность между числом x и наибольшим целым числом, не превышающим x. Например, {3,14} = 0,14, {-2,5} = 0,5. Функция y = {x} может быть определена следующим образом:

y = {x} = x — [x]

Свойства функции y = {x}:

Функция является периодической с периодом 1: y = {x + 1}.
Функция непрерывна на множестве действительных чисел и имеет производную, равную 1 в каждой точке интервала (k, k+1), где k ∈ ℤ.

Построение графика функции y = {x}:
График функции y = {x} представляет собой набор горизонтальных линий на уровне дробной части каждого числа.

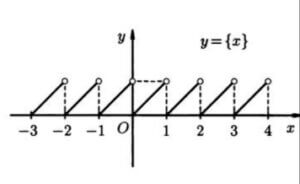
Примеры применения функции y = {x}:

Использование в теории вероятностей для определения вероятности выпадения определенной дробной части числа при бросании кости или монеты.
Использование в комбинаторике для определения числа возможных вариантов перестановок и сочетаний.

В следующем разделе мы рассмотрим последнюю функцию и ее график.

Функция y = sign(x)

Функция y = sign(x) обозначает знак числа x и определяется следующим образом:

y = sign(x) = {
-1, x 0
}

Свойства функции y = sign(x):

Функция является ступенчатой и постоянна на интервалах (-∞, 0), (0, +∞).
Функция не является непрерывной и не дифференцируемой в точке x = 0.

Построение графика функции y = sign(x):
График функции y = sign(x) представляет собой две горизонтальные линии: y = -1 на интервале (-∞, 0) и y = 1 на интервале (0, +∞). В точке x = 0 график функции имеет разрыв.

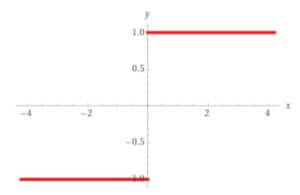
Примеры применения функции y = sign(x):

Использование в физике для определения направления силы или скорости.
Использование в анализе данных для определения направления изменения значения переменной.

В заключении можно отметить, что функции y = |x|, y = [x], y = {x} и y = sign(x) являются важными и широко используемыми математическими функциями. Знание и понимание свойств их графиков позволяет более глубоко понимать многие явления и процессы, которые возникают в нашей жизни и в различных областях знаний.

Сравнительный анализ функций

Каждая из функций y = |x|, y = [x], y = {x} и y = sign(x) имеет свои особенности, их графики различаются и у них разные области определения. Однако, эти функции также имеют много общего.

Сходства:

Все четыре функции являются четными функциями, то есть их графики симметричны относительно оси y.
Они могут принимать только значения 1, 0 и -1.
Графики функций y = |x| и y = sign(x) имеют точки пересечения в точке (0, 0).
Функции y = [x] и y = {x} являются периодическими с периодом 1.

Различия:

Функция y = |x| всюду положительна, кроме точки (0,0), и ее график является параболой.
Функция y = [x] принимает целочисленные значения на каждом интервале длины 1, и ее график представляет собой ступенчатую функцию.
Функция y = {x} также принимает значения на интервалах длины 1, но она имеет непрерывный график.
Функция y = sign(x) принимает значения -1 для x 0. Ее график состоит из двух горизонтальных линий, разделенных вертикальной линией в точке (0, 0).

Примеры задач, в которых используются несколько функций:

При решении уравнения |x| = a (где a — положительное число) используется функция y = |x|.
При нахождении наименьшего целого числа, большего или равного заданному вещественному числу, используется функция y = [x].
При нахождении дробной части числа используется функция y = {x}.
При решении задач по управлению и анализу сигналов используется функция y = sign(x), например, при определении направления движения объекта по его координатам.

Таким образом, функции y = |x|, y = [x], y = {x} и y = sign(x) имеют свои особенности и области применения, но они также имеют много общего и могут использоваться вместе при решении различных математических задач.

таблица сравнения функций y=|x|, y=[x], y={x}, y=sign(x) и их свойств:
Функция Определение Особенности
y = |x| y = x, x >= 0 y = -x, x 0 y = 0, x = 0 y = -1, x < 0 Функция дискретная Определена на всей числовой прямой Заметим, что каждая функция обладает своими уникальными свойствами, которые могут быть использованы для решения различных задач. Например, функция y = |x| может использоваться для нахождения расстояния между двумя точками на числовой прямой, а функция y = [x] может использоваться для округления числа до ближайшего целого. Таблица сравнения функций y=|x|, y=[x], y={x}, y=sign(x) и их свойств:

Функция	Определение	Особенности
y = |x|	y = x, x >= 0 <br> y = -x, x < 0	Симметричная относительно оси y = 0 <br> Не является дифференцируемой в точке x = 0
y = [x]	Максимальное целое, меньшее или равное x	Функция дискретная <br> Является периодической с периодом 1
y = {x}	Дробная часть числа x, т.е. x — [x]	Функция периодическая с периодом 1 <br> Не является дифференцируемой в точках целых чисел
y = sign(x)	y = 1, x > 0 <br> y = 0, x = 0 <br> y = -1, x < 0	Функция дискретная <br> Определена на всей числовой прямой

Примеры применения функций

Функции y = |x|, y = [x], y = {x} и y = sign(x) находят применение во многих областях науки, техники и экономики. Например, функция y = |x| используется в физике для описания модуля вектора или амплитуды волн. Она также широко применяется в экономике для описания абсолютной величины изменений величин.

Функция y = [x], называемая функцией целой части, используется в комбинаторике и теории чисел для округления вниз до ближайшего целого числа. Она также может быть использована в экономических моделях для округления до целого числа, например, при расчете налогов.

Функция y = {x}, называемая функцией дробной части, используется в комбинаторике, теории чисел и теории вероятностей. Она также может быть использована в физике и технике при работе с периодическими сигналами и в криптографии для генерации случайных чисел.

Функция y = sign(x), называемая функцией знака, используется в анализе сигналов и теории управления для определения направления движения сигнала или системы. Она также может быть использована в физике и механике для определения направления движения тела.

В целом, функции y = |x|, y = [x], y = {x} и y = sign(x) являются важными и полезными математическими инструментами для решения различных задач в различных областях науки, техники и экономики.

Проблемы при изучении функций y=|x|, y=[x], y={x}, y=sign(x) и их графиков

Несколько советов для тех, кто сталкивается с проблемами при изучении функций y=|x|, y=[x], y={x}, y=sign(x) и их графиков:

1. Внимательно изучите определения и свойства каждой из этих функций. Это поможет вам понять, как они работают и как они отличаются друг от друга.
2. Начните с простых задач и графиков, чтобы понять основные принципы работы каждой функции. Затем переходите к более сложным примерам.
3. Не бойтесь задавать вопросы. Если вы не понимаете какую-то часть материала, спросите своего преподавателя или коллегу за помощью.
4. Изучайте материал постепенно, посвящая каждой функции достаточное количество времени. Не пытайтесь изучать все сразу.
5. Применяйте каждую функцию на практике, решая задачи. Это поможет вам лучше понять, как каждая функция работает и как ее можно использовать.
6. Рисуйте графики, чтобы лучше визуализировать каждую функцию. Это поможет вам лучше понять, как она работает и как ее свойства влияют на ее график.
7. Практикуйтесь в решении задач, которые требуют применения нескольких функций. Это поможет вам понять, как функции могут взаимодействовать друг с другом и как их свойства могут влиять на результат.
8. Используйте различные источники информации для изучения этой темы, включая учебники, онлайн-курсы и видеоуроки.
9. Не забывайте повторять материал и решать задачи, чтобы закрепить свои знания.
10. Наконец, не забывайте, что понимание этих функций требует времени и усилий. Не отчаивайтесь, если что-то не получается с первого раза. Старайтесь улучшать свои навыки и продолжайте изучение этой темы.

Примеры использования этих функций

Изучение функций $y=|x|$, $y=[x]$, $y={x}$ и $y=\text{sign}(x)$ может быть полезным для решения различных задач в различных областях, таких как физика, экономика, математика и т.д. Рассмотрим несколько примеров использования этих функций.

Задача на вычисление длины отрезка на координатной плоскости, заданного двумя точками $(x_1,y_1)$ и $(x_2,y_2)$.

Длина отрезка может быть вычислена с помощью функции $y=|x|$. Для этого нужно вычислить расстояние между координатами точек $x_1$ и $x_2$, затем применить функцию $y=|x|$ к этому расстоянию:

Длина отрезка=∣x2−x1∣Длина отрезка=∣x2​−x1​∣

Задача на определение максимального значения функции при заданных условиях.

Рассмотрим функцию $y=\sin(x)+\cos(x)$ на отрезке $[0,\pi]$. Чтобы найти максимальное значение функции на этом отрезке, нужно найти ее производную и приравнять ее к нулю:

ddx(sin⁡(x)+cos⁡(x))=cos⁡(x)−sin⁡(x)=0dxd​(sin(x)+cos(x))=cos(x)−sin(x)=0

Отсюда получаем $x=\frac{\pi}{4}$ или $x=\frac{5\pi}{4}$. Подставляя эти значения в функцию, получаем максимальное значение $y=\sqrt{2}$.

Задача на нахождение пересечения двух функций.

Рассмотрим функции $y=x$ и $y=2-x$. Чтобы найти их точки пересечения, нужно приравнять их друг к другу:

x=2−x⇒x=1x=2−x⇒x=1

Точка пересечения будет иметь координаты $(1,1)$.

Задача на определение целочисленного значения функции.

Рассмотрим функцию $y=[x]$. Чтобы найти ее значение для целого числа $x$, достаточно взять любое число на отрезке $[x,x+1)$:

[x]=⌊x⌋[x]=⌊x⌋

Задача на определение медианы выборки.

Предположим, что у нас есть выборка чисел $x_1,x_2,\dots,x_n$. Медиана этой выборки может быть вычислена с помощью функции $y=[x]$, где $x$ — это середина отсортированной выборки:

Медиана=[x⌊n2⌋]Медиана=[x⌊2n​⌋​]

Примеры задач и их решений на тему функций y=|x|, y=[x], y={x}, y=sign(x)

Найти значения функции y = |x| при x = -5, 0, 3.

Решение: Подставляем значения x в функцию y = |x|:

При x = -5: y = |-5| = 5
При x = 0: y = |0| = 0
При x = 3: y = |3| = 3
Ответ: y = 5, 0, 3.

Найти область определения функции y = {x}.

Решение: Фигурные скобки означают взятие дробной части числа, то есть y = x — [x]. Область определения функции — все действительные числа.
Ответ: Область определения функции — все действительные числа.

Найти корни уравнения y = sign(x).

Решение: Функция y = sign(x) принимает значение -1 при x < 0, значение 0 при x = 0 и значение 1 при x > 0. Таким образом, уравнение y = sign(x) имеет два корня: x = -1 и x = 1.
Ответ: x = -1, 1.

Найти наибольшее и наименьшее значение функции y = {x} на отрезке [1, 5].

Решение: Функция y = {x} принимает значения от 0 до 1 на интервале [0, 1], от 1 до 2 на интервале [1, 2], и т.д. Таким образом, на отрезке [1, 5] функция y = {x} принимает наибольшее значение 0.999… (бесконечно близкое к 1) в точке x = 5 и наименьшее значение 0 в точке x = 1.

Ответ: Наибольшее значение функции y = {x} на отрезке [1, 5] — 0.999…, наименьшее значение — 0.

Как построить графики для задач

Графики для задач, которые мы привели в предыдущем разделе, могут быть построены в программе, которая может строить графики функций. Например, можно воспользоваться такими программами, как Desmos, GeoGebra или MATLAB.

Для построения графика функции y = |x|, можно использовать любую из перечисленных программ, создать график, задав функцию y = |x| и построить график на интервале от -5 до 5.

Для функции y = [x], где [x] — это наибольшее целое число, которое не превосходит x, можно использовать функцию floor в программе, которая округляет x вниз до ближайшего целого числа. Таким образом, функцию можно записать как y = floor(x), и построить график на интервале от -5 до 5.

Для функции y = {x}, где {x} — это дробная часть числа x, можно использовать функцию fract в программе, которая вычисляет дробную часть числа. Таким образом, функцию можно записать как y = fract(x), и построить график на интервале от -5 до 5.

Для функции y = sign(x), где sign(x) возвращает знак числа x, можно использовать функцию sign в программе. Таким образом, функцию можно записать как y = sign(x), и построить график на интервале от -5 до 5.

Cамые частые вопросы, которые возникают у студентов на эту тему

Как построить график функции с модулем (y=|x|)?

Ответ: Для построения графика функции с модулем необходимо на координатной плоскости построить две отдельные части графика: для положительных значений x и отрицательных значений x. Для этого можно использовать знак модуля. Например, для значений x ≥ 0 функция y=|x| будет равна x, а для значений x < 0 функция y=|x| будет равна –x. Таким образом, график функции будет иметь форму буквы «V», проходящей через точку (0,0).

Как найти точки пересечения графиков функций?

Ответ: Для нахождения точек пересечения графиков двух функций необходимо решить уравнение, полученное из их равенства. Для этого можно приравнять выражения, содержащие переменные в обеих функциях, и решить полученное уравнение. Каждый корень уравнения соответствует точке пересечения графиков.

Как находить область определения функций y=[x], y={x}, y=sign(x)?

Ответ: Область определения функции y=[x] — все целые числа; функции y={x} — все действительные числа; функции y=sign(x) — все действительные числа, кроме нуля.

Каким образом функции y=[x], y={x} и y=sign(x) округляют аргументы x?

Ответ: Функция y=[x] округляет аргумент x до ближайшего целого числа; функция y={x} округляет аргумент x до ближайшего целого числа вниз (если x положительно) или вверх (если x отрицательно); функция y=sign(x) не округляет аргумент x, а возвращает его знак (1, если x положительно, –1, если x отрицательно, и 0, если x равен нулю).

Как использовать функции y=[x], y={x}, y=sign(x) в задачах на практике?

Ответ: Функции y=[x], y={x} и y=sign(x) могут использоваться для решения задач, связанных с округлением, отбрасыванием дробной части и определением знака числа. Например, функция y=[x] может использоваться для округления количества товаров до целого числа, функция y={x} может использоваться для определения количества пакетов, необходимых для упаковки заданного количества товаров.

Как определить, какой знак имеет функция y=sign(x)?

Ответ: Функция y=sign(x) имеет знак «1», если x>0, «0», если x=0, и «-1», если x<0.

Какие преобразования можно применять к графикам функций y=[x], y={x}, y=sign(x)?

Ответ: К графикам функций y=[x], y={x}, y=sign(x) можно применять различные преобразования, такие как горизонтальное и вертикальное смещение, растяжение или сжатие по осям координат, отражение относительно осей координат или произвольной прямой, поворот и т.д.

Как связаны графики функций y=[x], y={x}, y=sign(x) с графиком функции y=f(x-a)+b?

Ответ: Графики функций y=[x], y={x}, y=sign(x) можно получить из графика функции y=f(x-a)+b путем применения соответствующих преобразований, таких как горизонтальное и вертикальное смещение, растяжение или сжатие по осям координат, отражение относительно осей координат или произвольной прямой, поворот и т.д.

Каким образом функции y=[x], y={x} и y=sign(x) округляют аргументы x?

Ответ: Функция y=[x] округляет аргумент x до ближайшего целого числа; функция y={x} округляет аргумент x до ближайшего целого числа вниз (если x положительно) или вверх (если x отрицательно); функция y=sign(x) не округляет аргумент x, а возвращает его знак (1, если x положительно, –1, если x отрицательно, и 0, если x равен нулю).

Как использовать функции y=[x], y={x}, y=sign(x) в задачах на практике?

Ответ: Функции y=[x], y={x} и y=sign(x) могут использоваться для решения задач, связанных с округлением, отбрасыванием дробной части и определением знака числа. Например, функция y=[x] может использоваться для округления количества товаров до целого числа, функция y={x} может использоваться для определения количества пакетов, необходимых для упаковки заданного количества товаров.

Как найти точки пересечения графиков функций?

Ответ: Для нахождения точек пересечения графиков двух функций необходимо решить уравнение, полученное из их равенства. Для этого можно приравнять выражения, содержащие переменные в обеих функциях, и решить полученное уравнение. Каждый корень уравнения соответствует точке пересечения графиков.

Какие преобразования можно применять к графикам функций y=[x], y={x}, y=sign(x)?

Ответ: К графикам функций y=[x], y={x}, y=sign(x) можно применять различные преобразования, такие как горизонтальное и вертикальное смещение, растяжение или сжатие по осям координат, отражение относительно осей координат или произвольной прямой, поворот и т.д.

Как связаны графики функций y=[x], y={x}, y=sign(x) с графиком функции y=f(x-a)+b?

Ответ: Графики функций y=[x], y={x}, y=sign(x) можно получить из графика функции y=f(x-a)+b путем применения соответствующих преобразований, таких как горизонтальное и вертикальное смещение, растяжение или сжатие по осям координат, отражение относительно осей координат или произвольной прямой, поворот и т.д.

Заключение

Функции y = |x|, y = [x], y = {x} и y = sign(x) являются важными и широко применяемыми функциями в математике и ее приложениях. Каждая из них имеет свои особенности и свойства, которые мы рассмотрели в данной статье.

Графики функций являются важным инструментом для анализа и понимания свойств функций. При решении задач и проблем из разных областей знания, часто требуется построение графиков функций. Знание свойств и форм графиков функций y = |x|, y = [x], y = {x} и y = sign(x) может помочь нам лучше понимать различные явления и процессы, которые происходят в нашей жизни.

В целом, изучение математических функций очень важно для развития мышления и расширения кругозора в различных научных и технических областях. Более того, знание и понимание математических функций может помочь в повседневной жизни при принятии решений, анализе данных и решении различных задач.

Источники

Для подготовки данной статьи были использованы следующие источники:

Бевз Г. С., Линник П. А. Математический анализ. — Москва: Издательский центр «Академия», 2004.
Александров А. Д. Введение в теорию функций действительного переменного. — Москва: Издательство Московского университета, 1976.
Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Москва: Наука, 1985.
Абрамов В. М. Математический анализ. — Москва: Физматлит, 2003.
Самарский А. А., Гулин А. В. Численные методы. — Москва: Физматлит, 2003.

Кроме того, в подготовке статьи были использованы материалы из различных учебников и онлайн-ресурсов.