Как найти длину вектора
При решении различных задач в геометрии возникает необходимость определить длину заданного вектора. Для того чтобы ее найти, нужно знать координаты начальной и конечной точки направленного отрезка. Далее все расчеты производятся по формуле, которую достаточно легко вывести, если правильно применить теорему Пифагора.
Понятие длины вектора
Прежде чем перейти к определению длины вектора, необходимо разъяснить само понятие «вектор». В геометрии оно используется для обозначения такого объекта, который характеризуется направлением и величиной. Его можно представить в виде отрезка. Далее необходимо пояснить то, как он выглядит на плоскости.
Отрезком в геометрии называют какую-то часть прямой, ограниченную двумя точками. У него может быть всего два направления, для обозначения которых используются такие понятия как начало и конец отрезка, которые соответствуют его границам. Направление принято указывать от начала отрезка к его концу.
Называть отрезок вектором можно в том случае, если известно, какая из двух его границ является началом, а какая – концом.
В геометрии он может обозначаться двумя буквами, соответствующими его началу и концу.
Если обозначается как \[\vec{A B}\], то A – это начало отрезка, а B – соответственно его конец.
Также допустимо обозначение в виде одной строчной буквы, например \[\vec{a}\]. На рисунке показано как это выглядит на плоскости.
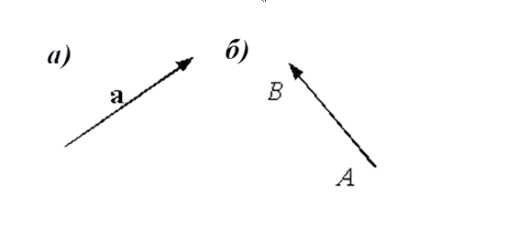
После того, как стало понятно, что такое вектор и как он обозначается, можно переходить к определению его длины.
Понятие длины вектора \[\vec{a}\] используется для обозначения размера направленного отрезка. Она обозначается, как \[|\vec{a}|\].
При решении задач в геометрии необходимо знать, в каких случаях применимо понятие равенство двух векторов.
Для того чтобы можно было назвать два вектора равными, должны соблюдаться два определенных условия:
- они являются сонаправленными;
- длина одного равна длине другого.
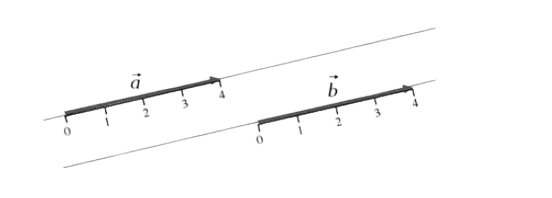
Определять векторы можно только в том случае, если введена система координат и ней у направленных отрезков имеются точные координаты.
Любой вектор независимо от его обозначения и длины можно разложить следующим образом:
\[\vec{c}=m \vec{i}+n \vec{j}\], где m и n — это какие-то действительные числа, а \[\vec{i}\] и \[\vec{j}\] – это два единичных вектора, расположенных непосредственно на осях \[O x\] и \[O y\].
Координатами рассматриваемого вектора \[\vec{c}=\vec{mi}+\vec{nj}\] в введенной нами прямоугольной системе координат будут являться коэффициенты его разложения. В математическом виде это записывается следующим образом:
\[\bar{c}=m, n\]
Формула длины вектора
Для того чтобы определить длину произвольного вектора, необходимо вывести формулу на основании точных данных координат этого отрезка в квадратной системе координат.
Чтобы понять, как это сделать, рассмотрим соответствующую задачу.
Координаты заданного вектора \[\vec{a}-x, y\]. Требуется определить его длину по указанным данным.
Решение:
Для того чтобы приступить к решения примера требуется ввести на плоскости систему координат \[x O y\]. Далее нужно будет отложить в введенной системе координат \[\vec{OA}=\vec{a}\]. После этого можно приступить к построению проекций \[O A_{1}\] и \[O A_{2}\], направленного отрезка, которой расположен на оси \[O x\] и \[O y\] так, как показано на рисунке ниже.
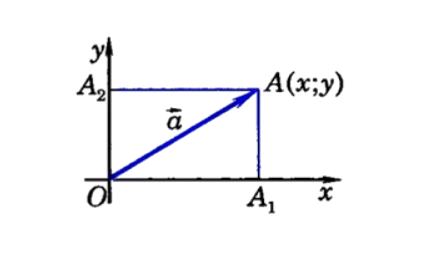
\[\vec{OA}\] будет для точки A радиус вектором. Это означает, что она будет иметь следующие координаты — x, y. Исходя из этого можно сделать вывод, что \[\left[O A_{1}\right]=x,\left[O A_{2}\right]=y\].
Для того чтобы определить длину, применяем теорему Пифагора. В результате получаем:
\[\begin{aligned}
&\left| \vec{a}\right|^{2}=\left[\mathrm{OA}_{1}\right]^{2}+\left[\mathrm{OA}_{2}\right]^{2} \\
&\left.|\vec{a}\right|^{2}=x^{2}+y^{2} \\
&\left.|\vec{ a}\right|^{2}=\sqrt{x^{2}+y^{2}}
\end{aligned}\]
Ответ: Искомая длина заданного вектора определяется по формуле \[\left.|\vec{a}\right|^{2}=\sqrt{x^{2}+y^{2}}\]
На основании рассмотренного примера можно сделать вывод, что для определения длины какого-либо вектора, у которого известны координаты, следует найти корень из суммы квадратов заданных координат.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры задач
Требуется определить расстояние между двумя точками X и Y, координаты которых (−1,7) и (8,4), соответственно.
Решение. Известно, что любые две точки на плоскости можно связать с понятием направленного отрезка. В данном случае мы будем рассматривать вектор \[\vec{X Y}\]. Как было сказано ранее, координаты определяются путем вычитания координат конца отрезка \[(Y)\] из соответствующих координат его начальной точки \[(X)\].
Применяя это правило, получаем: \[\vec{X Y}=(8+1,4-7)=(9-3)\]
Затем, чтобы найти искомую длину, применим формулу, выведенную нами ранее.
Получаем: \[d=\sqrt{9^{2}+(-3)^{2}}=\sqrt{81+9}=\sqrt{90}=3 \sqrt{10}\]
Ответ: Длина вектора равна \[3 \sqrt{10}\]
Важно! Эта задача позволяет вывести формулу для определения расстояния между начальной и конечной точками. Пусть они имеют следующие координаты \[\left(x^{\prime}, y^{\prime}\right)\] и \[\left(x^{\prime \prime}, y^{\prime \prime}\right)\]. Тогда определить длину между этими точками можно с помощью формулы:
\[d=\left(\mathrm{x}^{\prime}-\mathrm{x}^{\prime \prime}\right) 2+\left(y^{\prime}-y^{\prime \prime}\right)\]
Пусть нам дан один треугольник и известны координаты его вершин (6,-10),(13,-3),(5,0). Требуется найти периметр фигуры.
Решение. Сначала найдем длины сторон треугольника, используя выведенную формулу.
Длина первой стороны равна: \[\sqrt{(6-13)^{2}+(-10+3)^{2}}=\sqrt{(-7)^{2}+(-7)^{2}}=\sqrt{98}=7 \sqrt{2} .\]
Вторая сторона треугольника будет равна: \[\sqrt{(6-5)^{2}+(-10-0)^{2}}=\sqrt{1^{2}+(-10)^{2}}=\sqrt{101}\].
Третья сторона треугольника равняется: \[\sqrt{(13-5)^{2}+(-3-0)^{2}}=\sqrt{8^{2}+(-3)^{2}}=\sqrt{73}\].
Сложив все три стороны, получим длину периметра рассматриваемого треугольника.
Ответ: \[7 \sqrt{2}+\sqrt{101}+\sqrt{73}\].
Заключение. В процессе решения задач мы вывели формулу длины вектора, и научились применять ее для определения периметра геометрических фигур.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)