Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника
Нахождение периметра квадрата
Квадрат – это такой четырехугольник, который обладает свойствами прямоугольника, параллелограмма, а также ромба:
- Все стороны равны.
- Все углы прямые, то есть по 90°.
- Диагонали равны, а угол их пересечения прямой.
- Диагонали при пересечении делать эти углы пополам.
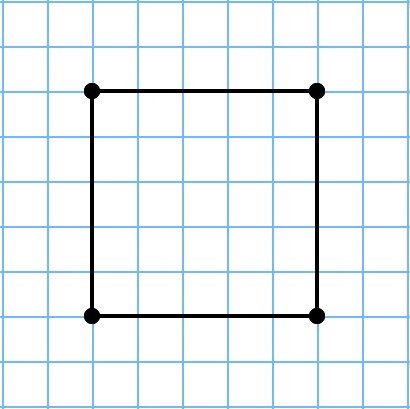
Зная свойства квадрата, можно понять, что его периметр находится путем сложения всех 4 сторон или же умножения его одной стороны на 4. Из этого выведем формулу где a – сторона квадрата:
\[P = a + a + a + a\]
\[P = 4a\]
Пример 1
Найдите периметр квадрата, сторона которого равна 6 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + a + a
6 + 6 + 6 + 6 = 24 (см)
Ответ: периметр этого квадрата равен 24 см.
Пример 2
Найдите периметр квадрата, сторона которого равна 10 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 4a
4 × 10 = 40 (см)
Ответ: периметр равен 40 см.
Нахождение периметра прямоугольника
Прямоугольник – это геометрическая фигура, которая может быть квадратом, прямоугольником или же ромбом.
Характеристики:
- У прямоугольника все углы по 90°
- В отличие от квадрата, у прямоугольника равны только противолежащие стороны, которые являются его шириной и высотой. Эти стороны параллельны. Из этого следует, что каждый квадрат – прямоугольник, но квадратом являются не все прямоугольники.
- Его прилегающие стороны перпендикулярны во всех случаях.
- Если провести диагональ, то она поделит прямоугольник на два равных прямоугольных треугольника.
- Если мы имеем две диагонали, то можно утверждать, что они одинаковой длины.
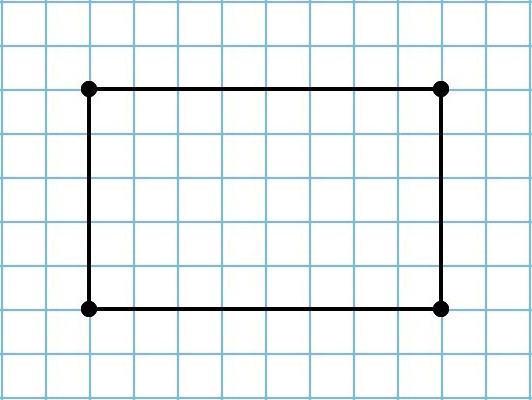
Периметр прямоугольника – это сумма длин всех его сторон. Получается, чтобы найти его периметр, воспользуемся формулами, в которых a – ширина и b – высота:
\[P = a + a + b + b\]
\[P = 2(a + b)\]
\[P = 2a + 2b\]
Пример 1
Найдите периметр прямоугольника, стороны которого равны 8 и 4 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + b + b
8 + 8 + 4 + 4 = 24 (см)
Ответ: периметр этого прямоугольника равен 24 см.
Пример 2
Найдите периметр прямоугольника, стороны которого равны 10 и 12 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 2(a + b)
2(10 + 12) = 44 (см)
Ответ: периметр равен 44 см.
Пример 3
Найдите периметр прямоугольника, стороны которого равны 9 и 7.
Решение:
На очереди третья формула. Подставим числа и решим:
P = 2a + 2b
2 × 9 + 2 × 7 = 32 (см)
Ответ: периметр равняется 32 см.
Нахождение периметра параллелограмма
Параллелограмм – это такой четырехугольник, у которого противоположные стороны парно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°
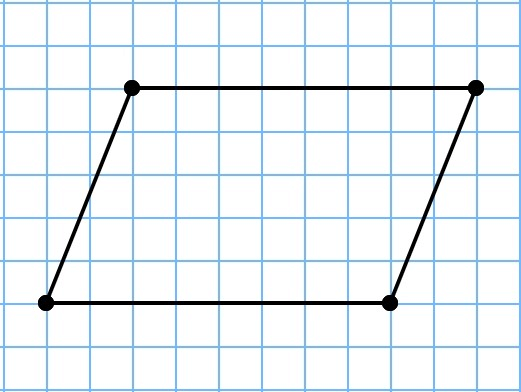
Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
\[P = a + a + b + b\]
\[P = 2(a + b)\]
\[P = 2a + 2b\]
Нахождение периметра трапеции
Трапеция – это четырехугольник, отличающийся тем, что его две стороны параллельны, а другие две не параллельны.
Характеристики:
- Основа трапеции – это те две параллельные стороны.
- Боковые стороны – не параллельные стороны.
- Если две боковые стороны равны, то можно сделать вывод, что такая трапеция равнобедренная.
- Трапеция с прямыми углами является прямоугольной.
- В трапеции можно провести среднюю линию, которая будет параллельна основаниям, а также равняться их полусумме.
- Если трапеция равнобедренная, то ее углы и длины диагоналей равны.
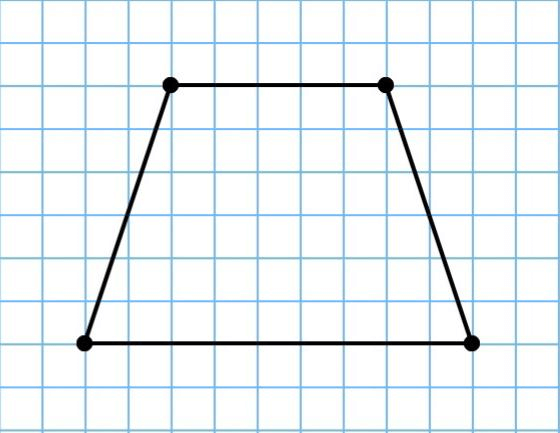
Чтобы найти периметр трапеции, необходимо знать длины всех ее сторон, чтобы сложить их. Представим, что
стороны трапеции – это a, b, c, d. Получается, для нахождения периметра трапеции, нам надо сложить все ее
стороны:
\[P = a + b + c + d\]
Пример 1
Найдите периметр трапеции, если известно, что ее стороны равны: 2, 6, 5, 5.
Решение:
Используем формулу:
P = a + b + c + d
2 + 6 + 5 + 5 = 18 (см)
Ответ: периметр трапеции равен 18 см.
Нахождение периметра ромба
Ромб – это четырехугольник, являющийся параллелограммом с равными сторонами.
Характеристики:
- Стороны и высоты ромба равны.
- Углы диагоналей при пересечении равны 90° — эти углы прямые.
- Диагональ является биссектрисой и делит углы пополам.
- Ромб называется параллелограммом, так как он имеет те же свойства, что и параллелограмм.
- В каждый ромб можно вписать окружность.
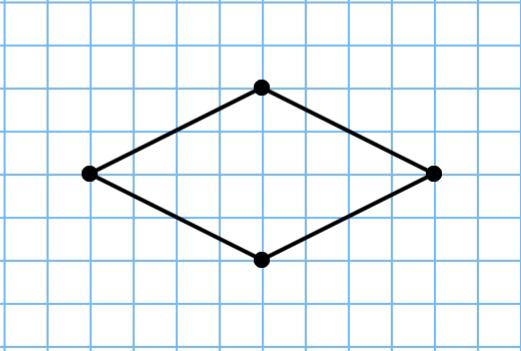
Ромб – это квадрат, а это значит, что найти его периметр можно так, как и периметр квадрата:
\[P = a + a + a + a\]
\[P = 4a\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нахождение периметра многоугольника
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.
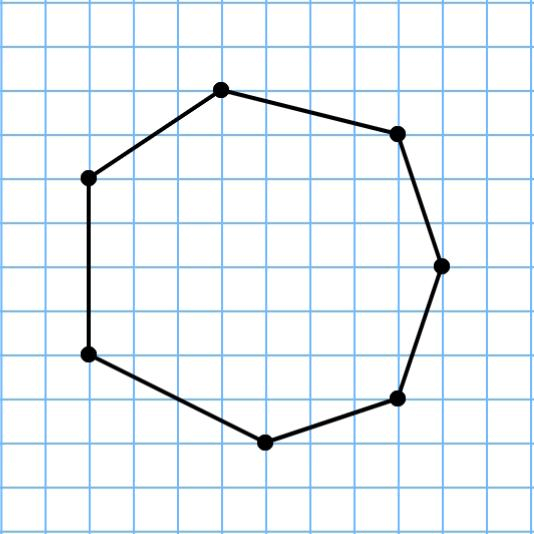
Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
\[P = a1 + a2 + … an\]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Нахождение периметра эллипса
Эллипс это замкнутая кривая, находящаяся на плоскости. Ее получают с помощью пересечения цилиндра плоскостью.
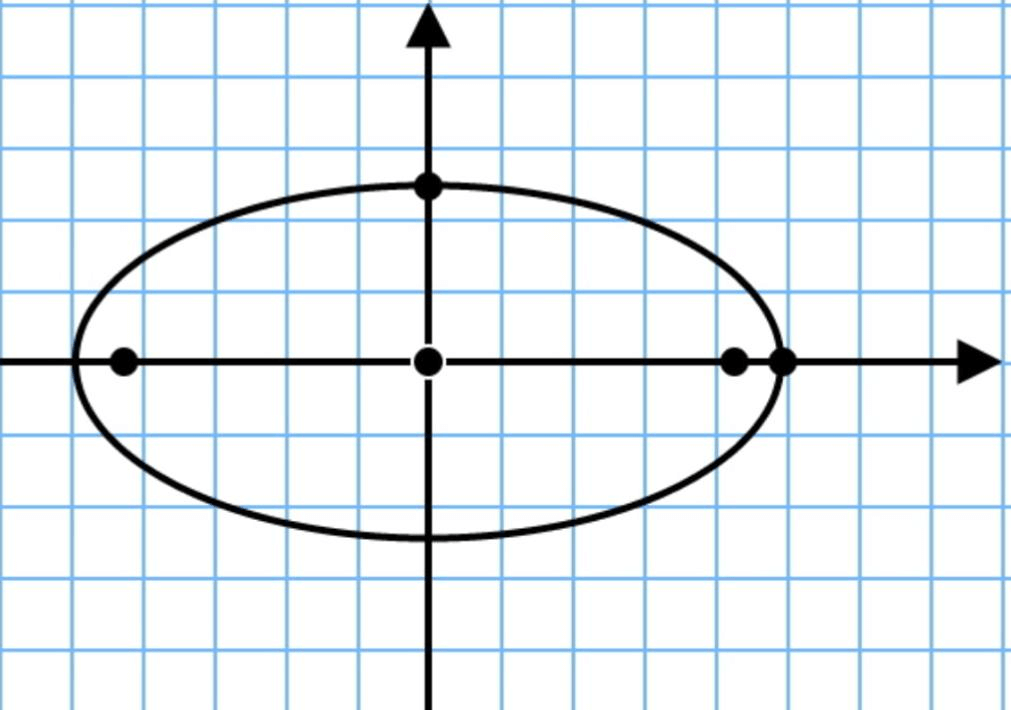
Для нахождения периметра, нужно следовать формуле:
\[P=4 \pi a b+a-b / a+b\]
Калькулятор периметр квадрата
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)