Теорема Пифагора
Основы теоремы Пифагора, формула и доказательство
Данная теорема издавна, является основой математики и в частности ее раздела — геометрии.
Основное определение теоремы Пифагора звучит следующим образом — сумма квадратов катета равна сумме квадрата гипотенузе для прямоугольного треугольника.
Теорема получила свое название в честь ученого, потому что именно он смог первый ее доказать.
Некоторые ученые, среди них, немецкий Контор, утверждали, что первое упоминание о теореме знали еще в древности. Поговаривали, что первыми о ней узнали Египтяне в 2200 году до нашей эры. Считали, что ранее прямые углы строили, благодаря треугольникам со сторонами 3,4,5.
Ранее теорема Пифагора звучала “теоремой невесты или нимфа”. данное название она получила с арабского языка. При переводе теоремы, ошибочно решили, что нимфа означает с перевода невеста.
Формула теоремы Пифагора имеет следующую запись:
a2+b2=c2
где стороны :
- a и b — стороны квадрата катетов;
- с — сторона гипотенузы.
Из данной формулы можно вывести следующие выражения:
Для геометрической фигуры, где с — самая длинная сторона, характерны следующие свойства:
- если c2 < a2 + b2 — в этом случае угол напротив стороны с является острым углом;
- если c2 = a2 + b2 — в этом случае, угол напротив стороны с является прямым;
- если c2 > a2 + b2 , следовательно угол, который относится к стороне с, имеет название тупого угла.
Доказательств теоремы существует множество с разными методами математического подхода. Самые известные из них:
- При помощи подобных треугольников;
- Метод площадей треугольников;
- Стандартное доказательство Евклида;
- Способ доказательства теоремы Леонардо да Винчи;
- При помощи площадей подобных треугольников;
- Методом бесконечности.
Однако, самая популярная методика доказательства, связанная с площадями подобных треугольников.
Соответственно все сложенные площади квадратов, которые построены при помощи катетов равны площади квадрата, который построен при помощи гипотенузы
Из этого следует, что площади данных квадратов равны – a2,b2,c2 . Именно так и звучит геометрическое доказательство теоремы Пифагора.
Подробное описание действий при доказательстве теоремы
Постараемся доказать, следующее уравнение: a2+b2=c2.
Изобразим прямоугольный треугольник со сторонами a, b, c.
- Необходимо прямоугольный треугольник изобразить в виде квадрата.
- От катета “а” продолжаем линию вверх на расстояние катета “b”.
- Затем проведем линию другого катета “а” вправо.
Получается такой же треугольник, только в перевернутом виде.
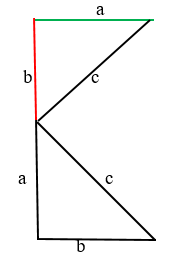
Таким же образом изображаем и с другой стороны. Проводим от катета (а) линию катета (b) и опускаем вниз отрезки (а) и (b).
Внизу от катета (b) проводим линию катета (а). В центре фигуры от каждого катета проводим гипотенузы (с).
Таким образом, при помощи построенных гипотенуз получился квадрат в центре фигуры.
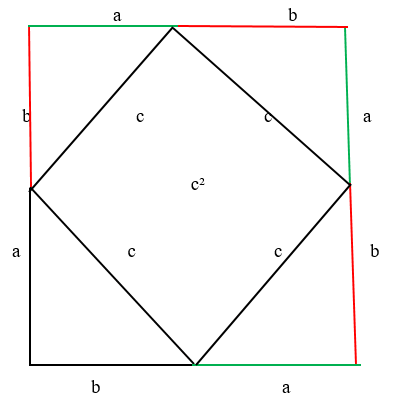
Полученный квадрат состоит из четырех прямоугольных треугольников. Площадь каждого треугольника равняется произведению его катетов.
A именно, \[\frac{1}{2} a b\].
Следовательно площадь квадрата в центре равняется квадрату гипотенузе c2, так как все четыре гипотенузы имеют сторону с длиной (с).
Из рисунка видно, что стороны квадрата (четырехугольника) имеют равные значения, следовательно, и прямые углы. Но, нужно доказать, что углы прямые.
Для этого построим квадрат:
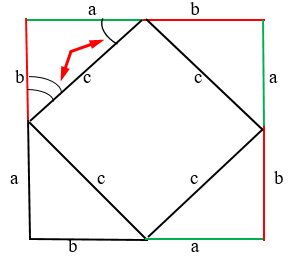
Видно, что два обозначенных угла имеет измерение по 90 градусов. Следовательно, если треугольники равны между собой, то и следующие углы так же буду прямыми. То есть равны предыдущим углам.
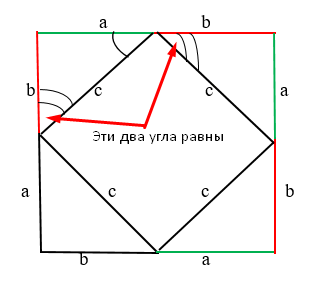
Суммарное значение углов равняется 90 градусов. Следовательно, предыдущий также равен 90 градусов. Таким правилом мы руководствуемся и с другой стороны.
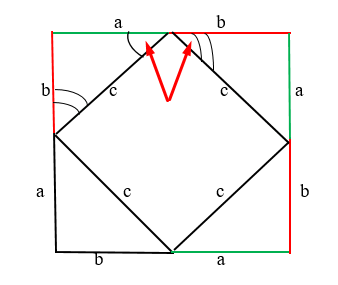
Сумма острых углов в треугольнике, который является прямоугольным равняется 90 градусам. Отсюда следует, что угол квадрата будет равен 90 градусов. Потому что три угла в сумме равняется 180 градусов.
Так как площадь квадрата состоит из: суммы равных площадей, прямоугольных треугольников и площади квадрата. Таким образом, получили фигуру со сторонами a и b.Нам известно, что площадь квадрата со стороной a и b – это будет квадрат его стороны. То есть (a+b)2.
- Записываем формулу: (a+b)2;
- Далее видим, что площадь прямоугольного треугольника равняется половине произведения его сторон катетов. Составляем выражение: \[(a+b)^{2} \cdot 4 \cdot \frac{1}{2}\].
- Затем к полученной формуле плюсуем площадь квадрата, который построен в центре фигуры треугольник со стороной. Выполнив перечисленные действия получаем следующее выражение: \[(a+b)^{2} \cdot 4 \cdot \frac{1}{2}+c^{2}\]
- Необходимо опустить скобки: a2+b2+2ab=2ab+c2
- Сокращаем уравнение и получаем выражение: c2=a2+b2

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Использование теоремы в решении
Пример №1
Вычертим прямоугольный треугольник со сторонами, длины которых равны 4 и 5 соответственно.
Необходимо найти значение гипотенузы. Обозначим ее буквой “с”
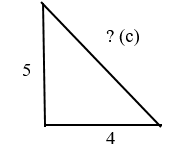
Решение примера:
Сумма квадратов катетов 52 + 42 равняется квадрату гипотенузы. В приведенной задаче это – c2 .
Применим на практике теорему Пифагора и подставим числовые данные: 52 + 42 = c2;
Подставив числовые значения и произведя расчет получаем следующие значения, 52=25 , а 42 = 16 . Суммарное значение катетов равняется 41.
Следовательно 41= c2. А именно: квадрат неизвестной стороны треугольника равен 41.
Выведем квадрат из числа 41 и получим значение 6,4.
Значение гипотенузы определено и равняется 6,4.
Ответ задачи: значение гипотенузы равно — 6,4.
Пример №2
Решение примера:
Для примера решения возьмем треугольник, где длина гипотенузы равняется 12, длина одного катета равна =10
Необходимо вычислить значение неизвестного нам катета.
Неизвестное значение стороны треугольника обозначим буквой – b.
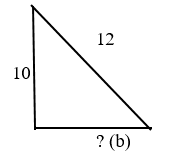
Воспользуемся теоремой Пифагора и определяем неизвестное значение, подставляя числовые данные в формулу.
102+b2=122
102=100, а 122=144;
Вычисляем уравнение и записываем следующее выражение:
100+b2 = 144;
Далее находим значение неизвестного катета в квадрате b2
b2 = 144 — 100;
b2=44;
Получаем b2=44, следовательно выводим квадрат числа и получаем значение b=6.6.
Ответ задачи: значение второго катета составляет 6,6















