Эллипс – уравнение, свойства, фокусное расстояние и эксцентриситет фигуры
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.
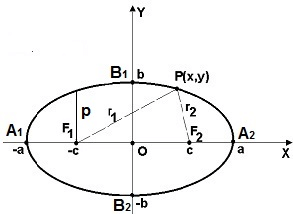
F1 и F2 – фокусы эллипса;
а – большая полуось;
b – малая полуось
с – фокусное расстояние
Фокусное расстояние эллипса и его полуоси связаны между собой соотношением \[\boldsymbol{a^{2}=b^{2}+c^{2}}\]
Доказательство:
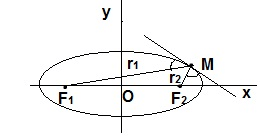
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что
r1 + r2 = 2*√(b2 + c2)
Когда точка M пересекает горизонтальную ось
r1 + r2 = а – c + а + c
По определению эллипса r1 + r 2 = const
Это позволяет после приравнивания получить
a² = b² + c²
r1 + r2 = 2а
Что и требовалось доказать.
Уравнение эллипса
Каноническим уравнением эллипса называют уравнение \[\boldsymbol{1=\left(x^{2} / a^{2}\right)+\left(y^{2} / b^{2}\right)}\]
Доказательство уравнения:
Введём прямоугольную декартову систему координат.
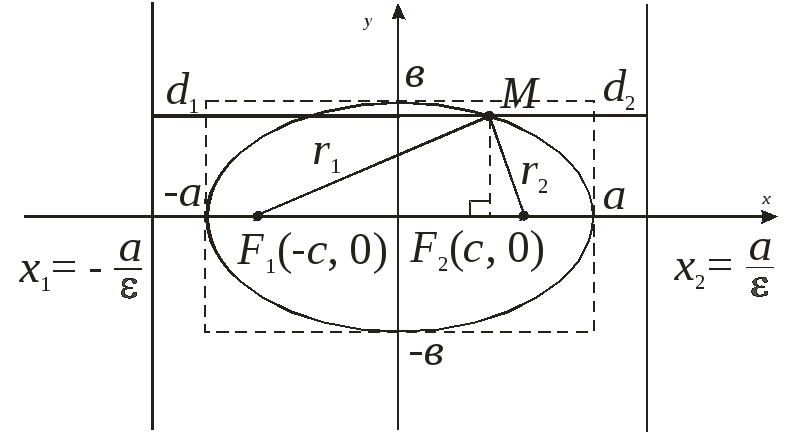
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.
- Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r1 + r2 = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.
r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]
Из этих уравнений получаем √[(x + c)2 + y2] + √[(x — c)2 + y2] = 2a
Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)2 + y2 = 4a2 – 4a√[(x — c)2 + y2] + (x – c)2 + y2
После сокращения приходим к 2xc = 4a2 – 4a√[(x-c)2 + y2] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)2 + y2] = a2 – xc
Возведём это выражение в квадрат
a2(x-c)2 + a2 y2 = a4 – 2a2xc + x2c2
Если раскрыть скобки и сократить на -2a2 xc, то a2x2 + a2c2 + a2y2 = a4 + x2c2
Отсюда легко получить (a2 – c2)x2 + a2y2 = a2(a2 – c2)
Из этого следует, что b2x2 +a2y2 = a2b2 - Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x2/a2) + (y2/b2)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y2 = b2(1- x2/a2)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r1 = √[(x + c)2 +y2] = √[x2 +2xc + c2 +b2 – b2x2/a2] = √[x2(1 – b2/a2) + 2xc +c2 +b2] =
= √[x2(a2 – b2)/a2 + 2xc + (c2 + b2)] = √[x2 (c2/a2) + 2xc +a2] = √[x(c/a) +a]2 = |a +xε|
т. е. r1 = |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r2.
Т. к. x2/a2 больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r1 = a + xε, r2 = a — xε
Из полученных равенств выходит, что r1 + r2 = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.
Свойства эллипса
- У эллипса имеются две взаимно перпендикулярные оси симметрии.
Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М1 (-x, y) и M2 (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M1 симметрична по отношению к оси X, а M2 по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии. - У эллипса есть центр симметрии.
Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии. - Эллипс пересекает каждую из осей в двух точках.
Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будет
r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]
Теперь давайте рассмотрим выражение
(x+-c)2 + y2 = x2 +- 2xc + c2+ y2 =
= x2 +- 2xc + a2 – b2 +y2 = x2 +- 2xc+ a2 — b2 + b2(1-x2/a2) =
= (a2 – b2)*x2/a2 +-2xc +a2 = c2*x2/a2+-2xa(c/a) + a2 = (a +c*x/a)2
Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F1M = a + εx и F2M = a – εx. Напомним, что ε – это эксцентриситет эллипса.
А теперь несколько свойств эллипса без доказательств.
- Эллипс можно получить, сжав окружность.
- Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
- Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
- Уравнение касательной к эллипсу в точке М, имеющей координаты xM и yM
1 = (x*xM)/a2 + (y*yM)/b2 - Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
- Угол между касательной к эллипсу и одним его фокальным радиусом (r1) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r2) фигуры.
Как построить эллипс
Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.
Построение эллипса по его большой и малой осям
Считается самым простым, не требующим серьёзных навыков.
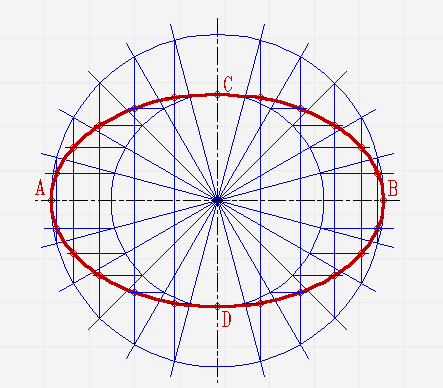
Проведите две перпендикулярные оси;
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;
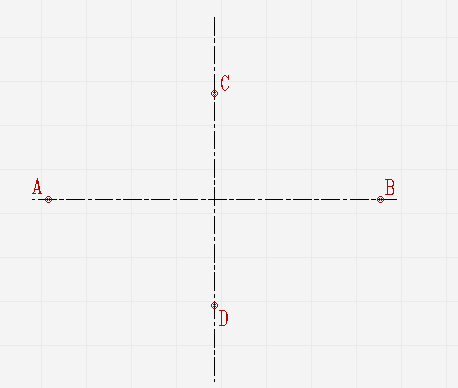
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;
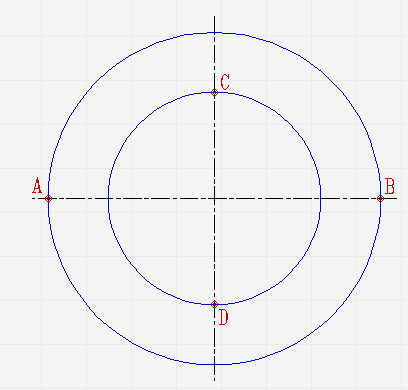
Проведите ещё диаметры в различных направлениях;
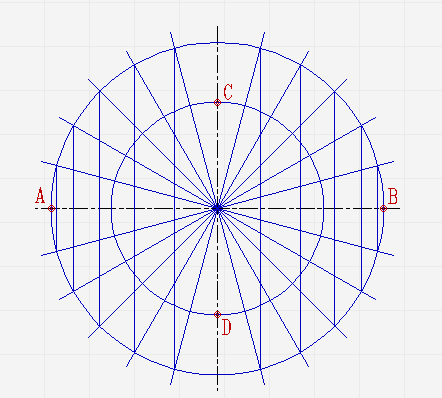
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;
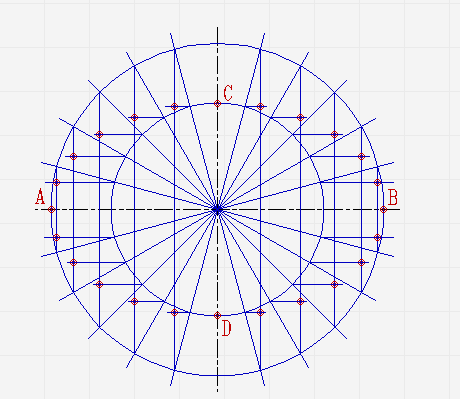
Соедините полученные точки плавной линией.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как построить эллипс с помощью циркуля
Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.
Порядок действий следующий:
- Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
- Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
- Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P1 и P2. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q1 и Q2. Отрезки P1P2 и Q1Q2 будут большой и малой полуосями будущего эллипса;
- Установите раствор циркуля на величину a. Поместите циркуль в точке Q1 или Q2. После этого обозначьте циркулем на отрезке P1P2 точки F1 и F2. Это будут фокусы фигуры.
- Отметьте на P1P2 любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P1. Затем начертите окружность данного радиуса из фокуса F1. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P2, но уже с центром из F2;
- Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P1P2;
- Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.
Примеры решения задач
Задача 1
Эллипс задан уравнением 16x2 + 25y2 = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.
Решение:
Разделим полученное уравнение на 400. Этим мы приведём его к виду
(x2/25) + (y2/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.
Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно
c=+-√(a2 – b2) = +-√(25-16) = +-3, а значит координаты фокусов будут
F1(-3,0) и F2 (3,0). Эксцентриситет ε = с/a = 3/5.
Ответ: a = 5, b = 4, ε = 3/5.
Задача 2
Выяснить, является ли эллипсом линия, заданная как
9x2 + 25y2 – 225 = 0
Преобразуем данное нам уравнение к каноническому виду. Для этого:
Перенесём 225 в правую сторону
9x2 + 25y2 = 225
Поделим обе части этого уравнения на 225
(9x2/225) + (25y2/225) = 1
Сократим дроби и получим
(x2/25) + (y2/9) = 1
Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.
Ответ: 9x2 + 25y2 – 225 = 0 является уравнением эллипса.
Задача 3
Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.
Решение:
Если большая ось равняется 10, значит полуось будет 5.
Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.
Далее нужно подставить и вычислить
4 = √(25-b2)
Возведём это уравнение в квадрат
16 = 25 – b2
Перенесём b2 влево, а 16 вправо
b2 = 25 – 16 =9
В результате этих не сложных преобразований и вычислений получим каноническое уравнение
(x2/25) + (y2/9) = 1
Ответ: (x2/25) + (y2/9) = 1.
Задача 4
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.
Решение:
Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси
c = √(169 – b2)
Возведём обе части уравнения в квадрат
c2 = 169 – b2
Отсюда
b2 = 169 – 144 = 25
Далее остаётся лишь составить каноническое уравнение
(x2/169) + (y2/25) = 1
Ответ: (x2/169) + (y2/25) = 1
Задача 5
Найти фокусы у эллипса, который задан уравнением (x2/25) + (y2/16) = 1
Решение:
Нам нужно найти число с, которое определяет первые координаты фокусов
c = √(25-16) =3
Фокусы заданного эллипса будут равны
F1(-3,0) и F2(3,0).
Ответ: F1(-3,0) и F2(3,0).















