Решение интегралов
Практическое применение интегралов в жизни
Реальный мир не идеален и не прямолинеен. В нем нет геометрических форм без изъяна, нет движения без ускорения. И зависимости между величинами редко представлены прямой линией. Поэтому вычисления не обходятся без интегралов.
Интеграл — важнейшее понятие математики. Связано с необходимостью отыскивать функции по их производным и измерять объемы и площади, работу сил за какой-либо промежуток времени.
Множество частных случаев из жизни делают интегрирование не просто полезным, а необходимым действием. Интеграл поможет:
- рассчитать стоимость, изучив зависимость потребности от предложений;
- вычислить время выполнения работы, с учетом усталости людей;
- узнать, как изменяется долг по кредиту в течение времени;
- определить прирост жителей города
Место интегралам нашлось не только в физико-математических науках, но и в астрономии, экономике, медицине, биологии и архитектуре.
Понимая практическую значимость интегралов, легче усвоить базовые понятия и применять их в решении задач.
Из истории интегрирования
Интегрирование рассматривается, как сложение бесконечно малых частей бесконечное количество раз.
Интегральный расчет получен при определении площадей и объемов. Правила измерения квадратуры были известны древним ученым. В Египте и Вавилоне вычисляли площади круга и объем усеченной пирамиды.
Значительный вклад внесли древнегреческие ученые. Первый метод интегрирования назвали «исчерпание» по аналогии с водой, которую черпают кружкой из ведра. В Древней Греции Архимед объяснил задачу вычисления площади круга без знаний о числе «Пи».
Описание метода
Для нахождения площади круга в него вписываются геометрические фигуры. Высчитывается предел последовательности площадей этих фигур, который и принимается за площадь круга.
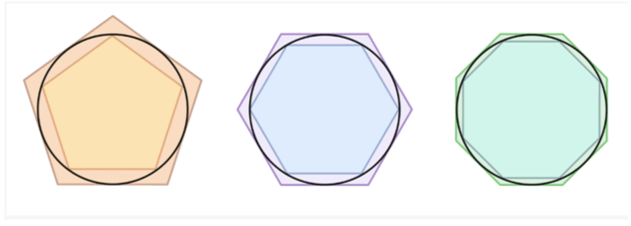
Данный способ вычисления площади рассматривает идею интегрирования. То есть нахождения предела безграничной суммы. Метод нашел применение в решении прикладных задач в разных научных областях.
Ньютон и Лейбниц сформулировали теорию интегрирования опираясь на законы дифференциального исчисления. Чтобы разобраться в классической теории нужно получить базовые знания.
Смысл интегрирования заключается в двух видах задач: геометрических и аналитико-алгебраических. В первом случае находят площади фигур, во втором подсчитывают суммарное значение переменной величины, принимающей различные значение единиц времени, длины и других измерений.
Понятие «Интеграл» в простом изложении
Термин «интеграл» произошел от латинского integer, то есть «целостный». Данный термин предложил математик Лейбниц еще в 17 веке.
Интеграл – это сложение маленьких частей и даже обозначение ∫ представляет собой вытянутую s, что означает сумму.
Интеграл – первообразная функции. Интегрирование – определение первообразной.
В математике интеграл вычисляет площадь, ограниченную кривой линией. Неопределенный интеграл – это вся фигура. Определенный интеграл – площадь некоторой части.
Запись интеграла функции:
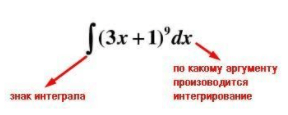
х – аргумент, его можно заменить любой другой переменной, в отношении которой будет осуществляться интегрирование. d – бесконечно малое число. Сочетание «dx» называют приращением и рассматривают, как бесконечно малый «икс».
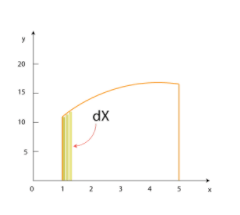
На рисунке криволинейная трапеция разбита на столбцы шириной х, число столбцов – d.
Неопределённый интеграл
Неопределенный интеграл – это сумма всех первообразных данной функции, которая не имеет границ интегрирования.
Сумма F(x)+C всех первоначальных функций f(x) на интервале а< x<b является неопределенным интегралом от функции f(x) на этом интервале и обозначается ∫f(x)dx .
Если функция F(x) является первообразной для f(x) , то по определению
∫ f(x)dx = F(x)+C
∫ — знак интеграла, f(x)dx — подынтегральное выражение, f(x) — подынтегральная функция, х — переменная интегрирования, С — произвольная постоянная.
Дифференцирование — процесс нахождения производной по данной функции или дифференциала. Обратный процесс – интегрирование. С помощью него по данной производной находят первоначальную функцию.
При нахождении неопределённых интегралов вычисляют первообразную и прибавляют «C».
Определённый интеграл
Определенный интеграл – это число, обозначающее площадь части фигуры. Значение аргумента ограничены промежутком a≤x≤b.
Определенный интеграл – это число, обозначающее площадь части фигуры. Значение аргумента ограничены промежутком a≤x≤b.
Обозначение \[\int_{a}^{b} f(x) d x\] читается, как «интеграл от а до b от функции f(х) по dx.
В графике на рисунке ограничения А и В обозначены на оси X.
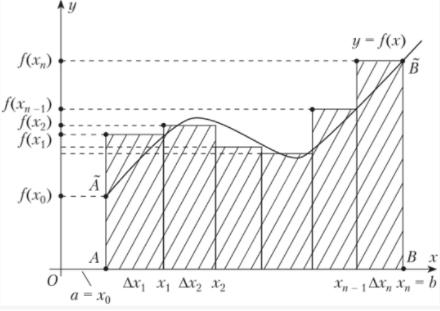
Определенные интегралы выражают площадь плоской фигуры, длину кривой, объем и поверхность тела, координаты центра тяжести, инерцию, работу.
Чтобы найти определенный интеграл, нужно вычислить первообразную, заменить значения «a» и «b» и посчитать разность. Связь между первообразной функцией и определенным интегралом выражает формула интеграла, Ньютона-Лейбница:
Таблица первообразных для решения интегралов.
Рассмотрим таблицу интегралов:

Правильное вычисление интегралов
Решение заданий с интегралом сводится к интегрированию функции по переменной. Когда интеграл имеет табличный вид, для решения нужна лишь таблица интегралов. В иных случаях необходимо упростить выражение, привести к табличной форме.
Прежде, чем приступить к преобразованию выражений с интегралами следует выучить основные свойства интегралов:
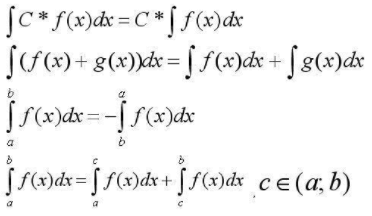
Простые способы преобразования выражений с интегралами помогут разобраться с более сложными теоремами и вычислениями интеграла:
Вынесение константы из-под знака интеграла:
Разложение на сумму интегралов суммы интеграла:
Знак интеграла изменится, при подмене а на b и b на а.
Разбиение интеграла на промежутки:

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления интегралов
Найти неопределенный интеграл.

Часто при решении используют тригонометрические формулы.
Решение определенного интеграла.
Давайте рассмотрим несколько примеров вычисления интегралов:
Пример 1.
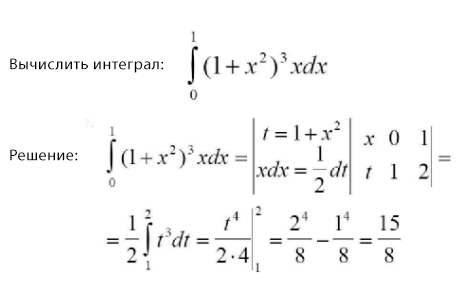
Пример 2.
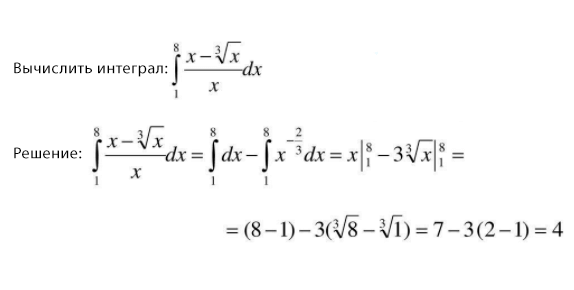
Словарь базовых понятий.
Для понимания сути интеграла необходимо разбираться в базовых понятиях: функция, производная, приращение, предел.
Функция – отношение между элементами, где изменение одного элемента, повлечёт изменение другого.
Производная – функция, которая описывает скорость трансформации второй функции в каждой данной точке. Вторая функция называется первообразной. По сути — это предел отношения приращения функции к приращению аргумента. Высчитывание проводят, используя таблицу производных со стандартными функциями.
Приращение – количественная степень изменения функции при вероятном изменении аргумента.
Предел – величина, к которой стремится значение функции, при стремлении аргумента к определённому значению.
Решение задач с интегралами могут показаться сложными. Выполнение практических заданий поможет преодолеть трудности.
Решение интегралов сводится к простым видоизменениям подынтегральной функции и поиску её в таблице интегралов.
Мы также можем отметить, что интегралы играют не последнюю роль в нашей жизни. В Биологических науках, к примеру, при их помощи узнают прирост популяции видов, в медицине используют в различных исследованиях, например, в томографии, в астрономии рассчитывают передвижение космических объектов и многое другое. Да и вообще трудно найти область, в которой не применяются данные методы вычисления.















