Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Нередко при решении задач в высшей математике требуется провести вычисление определителя матрицы. Для того, чтобы делать это правильно, нужно знать ключевые определения, свойства и различные вычислительные методы. В аналитической геометрии, математическом анализе, линейной алгебре и остальных разделах высшей математики специалисты применяют определитель матрицы.
Что такое матрица?
На первом шаге стоит чётко понимать, что матрица — типичная таблица, внутри которой
расположены цифры. Размерность — основополагающая характеристика матрицы, которая говорит о
том, сколько столбцов и строк прописано в матричной структуре. При этом определитель можно посчитать для
квадратной матрицы.Принято говорить, что та или иная матрица А имеет размер
[m x n], когда в ней расположено m строчек и n столбиков. Визуально это
выглядит следующим образом: \[A=[m \times n]\].
В некоторых случаях запись такая: \[A=\left(a_{i j}\right), \quad 1 \leq i \leq m ; \quad 1 \leq j \leq
n\].
7 свойств определителя
- Когда 2 строчки/столбца меняются местами, меняется знак у определителя на противоположный;
- В случае умножения одной строки/столбца на число k, весь определитель также умножится на данное число;
- Определитель будет неизменным в случае, если взять одну строку и сложить/отнять её любое количество раз из другой;
- В целом определитель равен 0, когда 2 строчки определителя равны, или пропорциональны, или одна из строчек заполнена нулями;
- Столбцы также имеют все эти свойства;
- Определитель будет неизменным, если матрица транспонируется;
- Определитель произведения матриц численно равен произведению определителей.
Как можно найти определитель матрицы второго порядка?
В основном студенты и ученики получают от преподавателей задание вычислить определитель матрицы второго, третьего, иногда четвёртого порядка. В первом случае решение типовое и достаточно понятное. Детально это происходит следующим образом:
это квадратная матрица второго порядка, определителем которой называется число
Посчитать определитель подобной матрицы можно здесь так:
В матрице 2-го порядка n = 2, отсюда следует, что факториал n! = 2! = 2. До момента применения формулы
важно разобраться с данными, которые мы получаем:
- k = 2;
- перестановки множеств 1,2 и 2,1;
- сколько инверсий в перестановке \[N_{k}\]: 0 и 1, так как 2 > 1;
- соотвествующие произведения. \[(-1)^{N_{k}} * a_{1 j 1(k)} * a_{2 j 2(k)}: a_{11} * a_{22}\] и \[-a_{12} * a_{21}\]
В итоге получаем:
Проанализировав ранее сказанное, получаем типовой алгоритм для нахождения определителя матрицы 2-го порядка 2х2:
Если рассмотреть данную формулу на наглядном примере, то это будет вот так:
Вычислить определитель матрицы \[2 \times 2\]:
\[A=\left|\begin{array}{cc}2 & 3 \\-6 & 1\end{array}\right|\]
Решение:
Итак, у нас получается \[a_{11}=2, a_{12}=3, a_{21}=-6, a_{22}=1\].
Для решения необходимо воспользоваться ранее рассмотренной формулой:
\[A=\left|\begin{array}{ll}a_{11} & a_{12} \\a_{21} & a_{22}\end{array}\right|=a_{11} * a_{22}-a_{12} * a_{21}\]
Подставляем числа с примера и находим:
\[A=\left|\begin{array}{cc}2 & 3 \\-6 & 1\end{array}\right|=2 * 1-3 *(-6)=3-(-18)=21\]
Ответ:
Определитель матрицы второго порядка = 21.
Чтобы упростить понимание процесса, как в данном случае находится определитель матрицы, можно представить такой расчёт: от произведения элементов основной диагонали отнимается произведение элементов другой диагонали.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Матрица 3-го порядка: методы нахождения ее определителя
Существует 2 способа, позволяющих быстро и точно решить уравнения. Определитель матрицы при этом находится по правилу треугольника или «параллельных полосок».
Правило треугольника
Визуальная схема действий здесь выглядит достаточно просто:
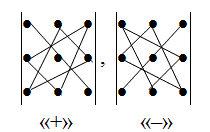
Произведения элементов в левом определителе, соединенные прямыми, суммируются; затем, перемноженные элементы правого определителя, связанные по прямой, вычитаются. Происходит это таким образом:
Правило Саррюса
Согласно правилу Саррюса («параллельных полосок»), матрица рассчитывается с учётом некоторых факторов и ряда операций:
- слева от определителя выписываются 2 первых столбца;
- элементы с основной диагонали и остальные, прописанные параллельно, перемножаются, произведения будут со знаком «+»;
- элементы с побочной диагонали и другие, которые ей параллельны, перемножаются, произведения будут со знаком «-».
Схематично это выглядит так:
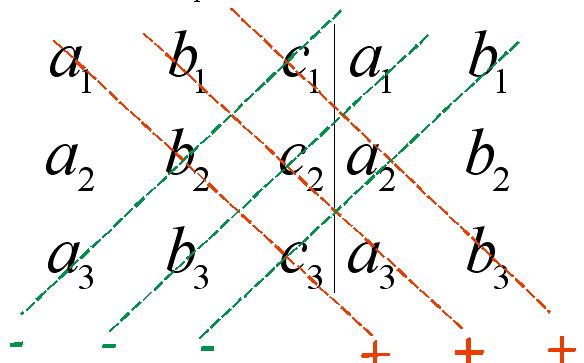
Расчёт идёт по формуле:
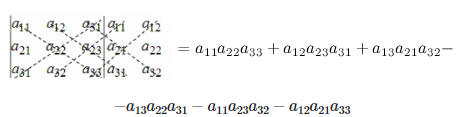
Вычислить определитель \[\left|\begin{array}{rrr}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2\end{array}\right|\] с
помощью правила Саррюса.
Решение:
\[\begin{array}{|rrr|rr}3 & 3 & -1 & 3 & 3 \\4 & 1 & 3 & 4 & 1 \\1 & -2 & -2 & 1 & -2\end{array} =3 \cdot 1
\cdot(-2)+3 \cdot 3 \cdot 1+\\+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4
\cdot(-2)=54\]
Ответ:\[\left|\begin{array}{rrr}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2\end{array}\right|=54\]
Разложение определителя по элементам строки или столбца
Определитель матрицы четвёртого порядка вычисляется двумя способами: разложение по элементам строки или столбца. Это — способ рассчитать определитель n как нахождение определителя порядка n-1, достаточно представить определитель как итог сложения произведений элементов строки/столбца на их алгебраические дополнения.
\[|A|=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}\](разложение по элементам 1-ой строки)
\[|A|=a_{12} A_{12}+a_{22} A_{22}+a_{32} A_{32}\](разложение по элементам 2-го столбца)
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)