Умножение матриц и алгоритм решения задач

Алгоритм умножения матриц в различных случаях

Умножаем данные в строке для первой матрицы на соответствующие данные в столбцах из второй матрицы.

• Перемножаем числовые значения первой строки на значения из первого столбца:

1. Производим умножение первого элемента первой строки на соответствующий элемент из первого столбца.
2. Находим произведение второго элемента первой строки и второго элемента, который берем из столбца №1.
3. Проделываем такие же действия со всеми элементами, до тех пор, пока не дойдем до конца первой строки матрицы.  
4. Вычисленные произведения необходимо сложить между собой.
5. Вычисленный результат будет равняться элементу для первой строки.

• Используя идентичный алгоритм, можно перемножить данные в первой строке из первой матрицы на данные всех последующих столбцов из второй матрицы. Вычисленные значения данных будет являться первой строкой матрицы, которую необходимо вычислить.

• Строка под номером два определяемой матрицы вычисляется также. Произведение числовых данных второй строки из первой матрицы на соответствующие данные для каждого столбца из второй матрицы. Окончательные данные фиксируются в составленную, новую матрицу, после окончания каждого определения суммы значений.
• Аналогичные действия нужно проводить с каждой строкой вычисляемой матрицы.  Вычисления проводятся до тех пор все строчки новой матрицы не будут заполнены значениями.

Правило умножения произведения двух и более матриц

Умножение двух матриц. Произведение матриц (С= А x В) —  является действием только для матриц А и В которые согласованы между собой. Для данных значений, число столбцов у матрицы А должно равняться количеству строк матрицы В:

\[m \cdot n\] \[m \cdot p\] \[p \cdot n\]

Примеры решения:

Пример №1:

Необходимо выполнить умножение двух матриц:

\[A=a_{i j}\] у которой размеры \[m \times n\] 

\[B=b_{i j}\] у которой размеры \[p \times n\] 

Необходимо вычислить матрицу C.

Элементы \[C_{i j}\].

Для вычисления применим формулу:

\[c_{i j}=a_{i 1} \cdot b_{i 1}+a_{i 2} \cdot b_{i 2}+\ldots .+a_{i p} \cdot b_{p j}, \mathrm{i}=1, \ldots . \mathrm{m}, \mathrm{j}=, \ldots . . \mathrm{m}\].

Умножение трёх матриц

Чтобы вычислить произведение трех матриц применяют два способа.

1. Определить AB и умножить на значение С: (АВ)*С;
2. Находим произведение ВС, затем умножаем полученное значение на А.

Пример №2:

Выполним умножение матриц двумя способами.

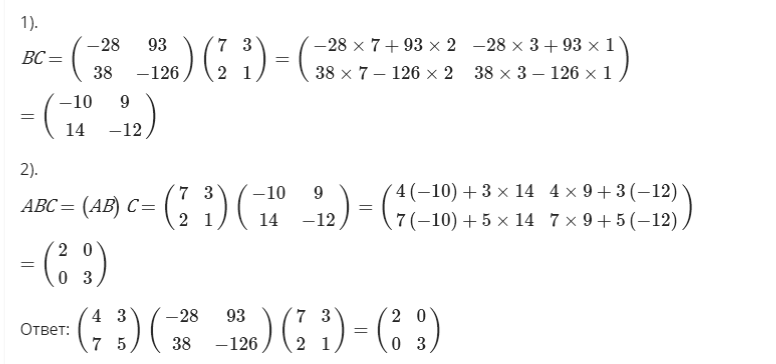
Умножение матрицы на число

Произведение значение матрицы, равное числу A на некое значение К, будет выглядеть следующим образом.

Размер будет таким же, как и в исходной матрице, который получен путем перемножения на заданное число все матричных элементов.

• \[1 \cdot A=A\]
• \[0 \cdot A=\] значение матрицы с нулевым результатом;
• \[k(A+B)=k A+k B\]
• \[(k+n) A=k A+n A\]
• \[(k \cdot n) \cdot A=k(n \cdot A)\]

Пример:

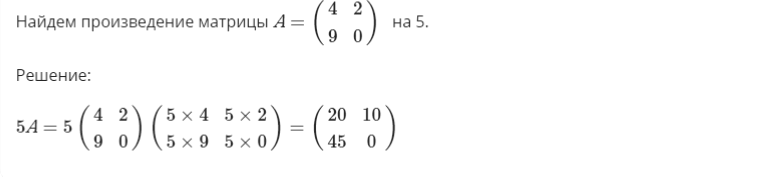
Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Принцип умножения матрицы на вектор значения

Для определения значения произведения матрицы и вектора, нужно использовать правило, которое звучит как: “умножение строки на столбе”

• при умножении матрицы на векторный столбец, значение столбцов в любой матрице обязательно должно совпадать с количеством строк в вектор-столбце.
• окончательным результатом произведения векторного столбца будет являться только вектор.

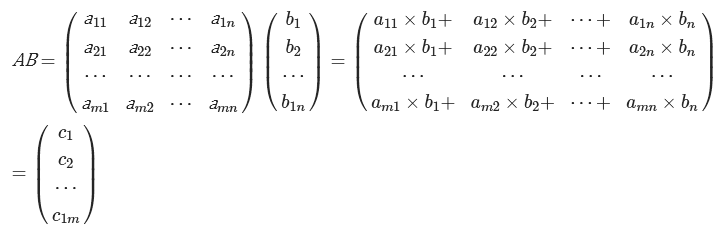
• в случае, когда перемножаем векторную строку, то матрица при умножении должна быть обязательно векторным столбцом. Количество столбиков обязательно должно совпадать со значение столбцов относительно строк.

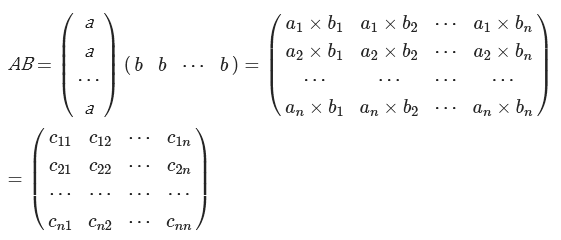
Пример решения задачи данного типа:

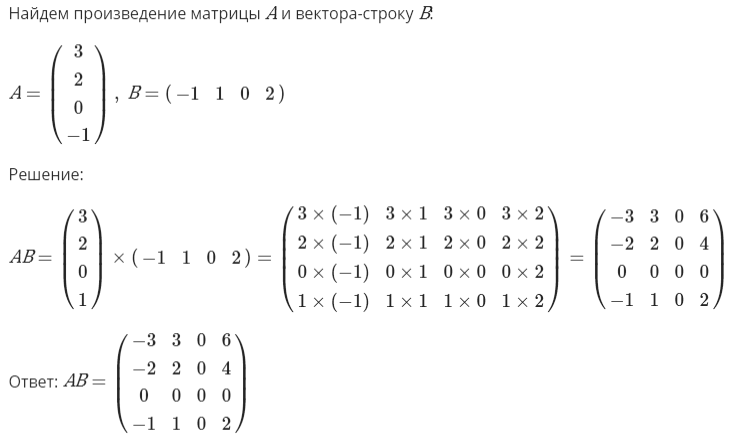
Возведение матрицы в степенное значение

Для того чтобы возвести значение матрицы в степень, необходимо выполнить следующее действие: перемножить все значения матрицы друг на друга.

Произведение для матричного значения будет актуально только в случае, когда: количество столбцов первой матрицы равняется числу таких же столбцов во второй матрице.

Возведение в степень возможно только для квадратной матрицы. Для этого применяют n-ую степень матрицы, и перемножают значение на себя n количество раз.

\[A^{2}=A \bullet A\],

\[A^{3}=A^{2} \bullet A=A \bullet A^{2}\],

\[A^{4}=A^{3} \bullet A=A^{2} \bullet A^{2}=A \bullet A^{3}\],

\[A^{n}=\underbrace{A \bullet A \bullet \ldots \bullet A}_{n \text { paз }} .\]

Пример: Дана матрица:

Найти A² и A³.

Основные свойства и правила умножения матриц

1. \[(A \times B) \times C=A(B C)-\] принцип сочетательного свойства при перемножении матричных значений.
2. \[A(B+C)=A B+A C-\] распределительное сочетание и распределение при перемножении матриц.
3. \[(A+B) C=A C+B C-\] аналогичные характерные действия, которые свойственны второму пункту.
4. \[\lambda(A B)=(\lambda A) B\].