Таблица интегралов

Для быстрого интегрального исчисления нужно знать, как искать производные простой и сложной функции. Ведь нахождение интеграла и производных являются взаимно обратные операции. Для интегрирования потребуются: таблица интегралов полная и также формулы интегралов таблица основных свойств, таблица производных и интегралов.

У многих возникает сложность в изучении и понимании неопределенных интегралов. Если производные обладают всего лишь 5 правилами дифференцирования, четким алгоритм, таблицей производных, то при интегрировании совсем иначе. Используются десятки приемов и способов интегрирования. При неверном выборе способа интегрирования и различного метода интеграл вычислять можно долго, так как он представляет собой некий ребус.

Определение первообразной

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство (F(x)+C)׳=f(x). Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Неопределенный интеграл имеет обозначение: \[\int f(x) d x=F(x)+C, c=\text { const }\].

Определение интегрирования

Дифференциал с интегральным выражением являются взаимно обратными действиями. У любой непрерывной на интервале функции есть какой-либо неопределенный интеграл.

Кратко о терминах и обозначениях:

Таблица интегралов:

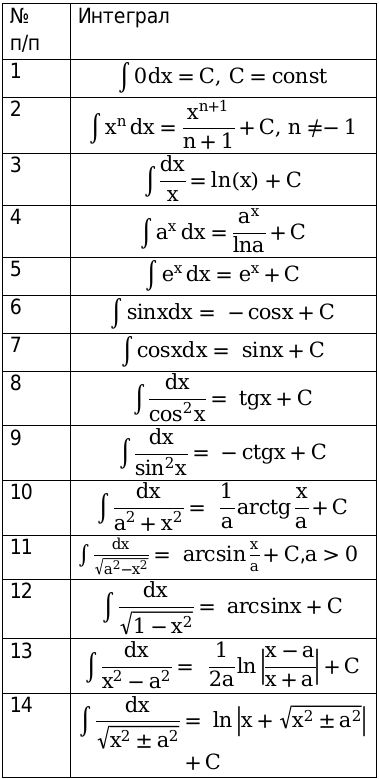
Таблица производных не включает формулы, которые соответствуют формулам из 10,13,14 таблицы. Чтобы проверить справедливость формул, необходимо произвести дифференцирование над ними.

Формулы интегралов, полная таблица основных свойств:

Расшифровка свойств интегралов:

1. Неопределенный интеграл при интегрировании функции является равным предоставляемой функции.
2. Производная от интегрального выражения будет равна подынтегральной функции, а дифференциал будет равен подынтегральному выражению.
3. Множитель в виде числа можно выносить за интеграл.
4. Интегральное выражение от суммы функций имеет такое же значение, как сумма интегральных выражений.
5. Подынтегральное выражение с множителями внутри равен подынтегральному выражению с выносимой константой.

C помощью них можно упростить выражение интеграла и вычислить элементарными действиями.

Стоит рассмотреть примеры для лучшего восприятия темы:

Вычислить интеграл и сделать проверку:

Вычислим интеграл, раскрывая скобки. При этом знак интеграла относится к каждому члену выражения.

Берем в использование свойство интеграла в этом же действии:

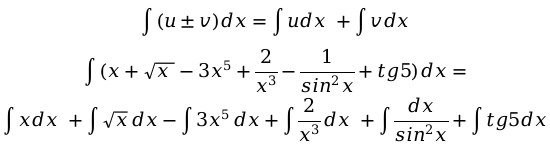
Вынесем все существуемые константы за знак интеграла — в данном случае они представляют собой числа. Стоит обратить внимание, что последнее выражение tg5 — это и является константа, её также выносим.

На этом этапе стоит преобразовать степени, корни для интегрирования. Как при дифференцировании, корни представляем в формате \[x^{\frac{a}{b}}\]. Степени и корни, которые стоят в знаменателе переносим наверх с противоположным знаком.

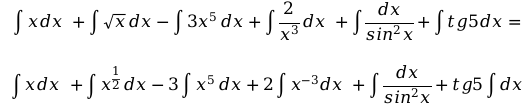
Используя таблицу основных интегралов, интегрируем:

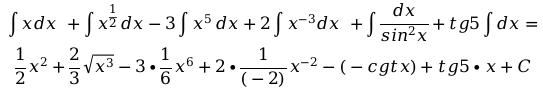
И окончательный ответ:

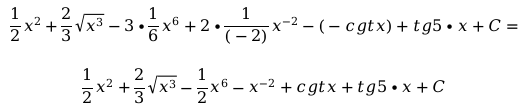
Примечание: В этом примере содержатся и используются только табличные интегралы. Все превращения осуществляются с помощью данных формул:

Стоит обратить внимание на формулу степенной функции: \[\int x^{n} d x=\frac{x^{n+1}}{n+1}+C, n \neq-1\], которая встречается почти в каждом примере.

Интеграл \[\int d x=x+C\] является частным случаем табличного интеграла: \[\int d x=\int x^{0} d x=\frac{1}{1} \cdot x^{1}+C=x+C\].

Константу C ставится только один раз в конечном выражении. Ставить после каждого интеграла не стоит. 

Выполним проверку. Для выполнения проверки необходимо продифференцировать найденное выражение, то есть найти производную:

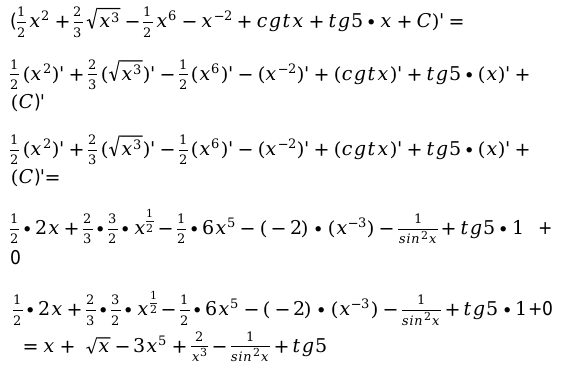
Если получилось исходное выражение, то интеграл был вычислен верно.

Раскрытие дифференциала происходит так:

1. знак d необходимо убрать; 
2. ставится штрих справа над скобкой, чтобы обозначить производную;
3. в конечное выражение добавляется множитель dx

Например: \[d(2 x-1)=(2 x-1)^{\prime} d x=(2-0) d x=2 d x\]

Проверить правильность табличного интеграла:

Решение:

Найдем производную от правой части выражения:

Производная получилось такая же, как и подынтегральная функция. Поэтому формула является верной.

Вычислить интеграл:

Решение:

Используем одно из основных свойств:

Используем свойство о вынесении множителя за интеграл:

С помощью таблицы:

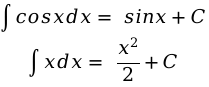
При вычислении воспользуемся 5 свойством:

Найдем ответ:

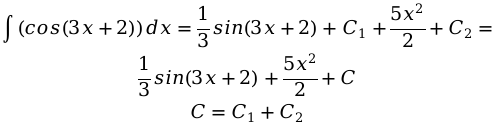
При этом C₁+C₂ являются частями C. Если отдельно решается 2 и более интегралов, то к каждому члену ставится C с определенным индексом.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь