Что такое биссектриса угла в геометрии

Напомним, что углом называют два луча, которые исходят из одной точки O. Для конкретики будем называть их лучами OA и OC. Из точки можно провести бесчисленное количество лучей, но среди них есть один особенный, именуемый биссектрисой угла.

Понятие биссектрисы угла

Определения 1 — 2

Биссектрисой угла в геометрии называют луч, начинающийся в его вершине и делящий указанный угол на две равные части (сектора). Сказанное хорошо видно на рисунке ниже. Для указания равенства двух углов, их отмечают одинаковым количеством дуг.

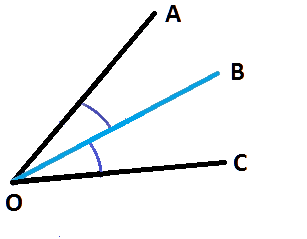
Определить биссектрису угла можно и по-другому, воспользовавшись одним из основных её свойств – все точки биссектрисы угла всегда, во всех случаях, равноудалены от сторон того угла, в котором она проведена.

---

Биссектрисой угла принято считать геометрическое место точек плоскости, находящихся на равном удалении от его сторон.

Свойства точки биссектрисы угла

Из определения 2 можно сделать два вывода:

1. Любая из точек биссектрисы угла находится на одинаковом удалении от его сторон;
2. Если точка имеет равные расстояния от двух сторон угла, то она непременно лежит среди точек его биссектрисы и принадлежит к их множеству.

Докажем эти два утверждения.

Определения 3 — 4

Расстоянием от точки M до проходящей в их общей плоскости прямой принято считать длину перпендикуляра, проведённого к M.

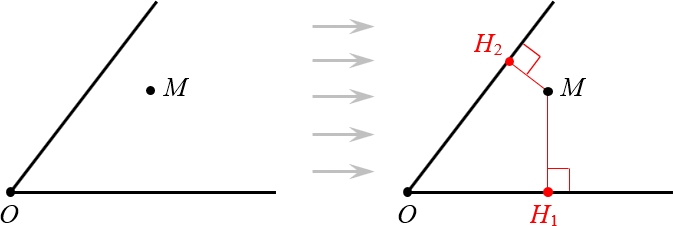
Т. к. луч является частью прямой, а угол создан двумя лучами, из определения выше очень легко понять, что является расстоянием от точки до сторон угла.

---

Расстоянием от точки до сторон угла называют длину перпендикуляров к лучам, которые образуют указанный угол.

Доказательство первого утверждения – расстояния от биссектрисы до сторон угла между собой всегда равны.

Проведём из М перпендикуляры к сторонам угла:

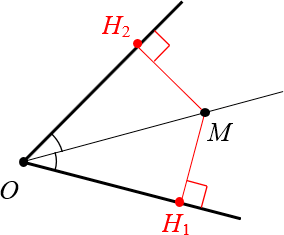
Так перед нами оказалось два прямоугольных треугольника, у которых имеется общая гипотенуза и равные углы.

• Угол MOH₁ равен углу MOH_2.
• Углы MH₁O и MH₂O являются прямыми. Это следует из построения.
• Углы OMH₁ и OMH₂ тоже прямые, ведь сумма углов в любом прямоугольном треугольнике за вычетом прямого всегда равняется 90 градусам.

Из сказанного следует, что треугольники равны по одной их стороне и прилежащим углам, а значит MH₁ = MH₂. Это нам и требовалось доказать.

Доказательство второго утверждения – если расстояния до M численно одинаковы, то она принадлежит биссектрисе.

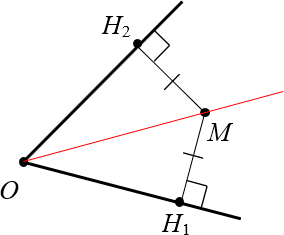
Мы опять имеем прямоугольные треугольники. У них, как видно из рисунка, имеется общая гипотенуза OM. Стороны MH₁ и MH₂ одинаковы по условию. Оставшиеся катеты тоже равны. Их легко вычислить, как OH₁² = OH₂²= OM² – MH₁². Получается, что треугольники равны по всем трём сторонам. Это значит, что равны и углы. Доказательство завершено.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Некоторые свойства биссектрисы угла