Формула нахождения вершины параболы
Понятие вершины параболы
Парабола – это геометрическое множество точек, которые равноудалены от точки F, и которая не является частью параболы и прямой, а также не проходит через центр отрезка.
Вершина параболы — это некая точка, которая расположена ближе всего в директрисе параболы. Данная точка является центром любого отрезка, который ограничен точками фокуса параболы и директрисой.
Каноническое уравнение параболы выглядит следующим образом:
\[y^{2}=2 p x\]
Где: \[p\] — параметр параболы; \[x\] — ось данной параболы.
Данное уравнение будет справедливо только для параболы, вершина которой проходит через центр осей.
Чтобы определить принадлежность точки к графику заданной параболы, нужно точку подставить в уравнение:
где:
- a, b, c — заданные коэффициенты;
- х — ось координатной прямой.
Определение вершины кубической параболы
Кубическая парабола – плоская алгебраическая кривая третьего порядка.
Ее каноническое уравнение в прямоугольной декартовой системе координат имеет вид у = ах3, где а ≠ 0.
Для кубической параболы характерен центр симметрии в самом начале координат. Данная точка является точкой перегиба кривой. Касательная к кубической параболе, в этой же точке именуется как ось абсцисс.
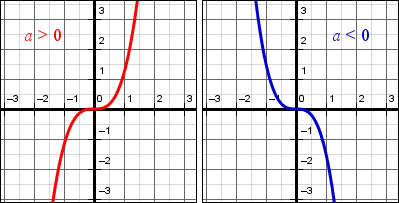
Для того, чтобы определить точки вершин кубической параболы, нужно вычислить ее производную. Точки вершин, иначе еще называют точками минимума и максимума.
После того, как определится производная, нужно ее значение приравнять к нулевому. Затем можно приступать к вычислению значений x и y.
Определение вершин параболы, которая задана квадратичной функцией
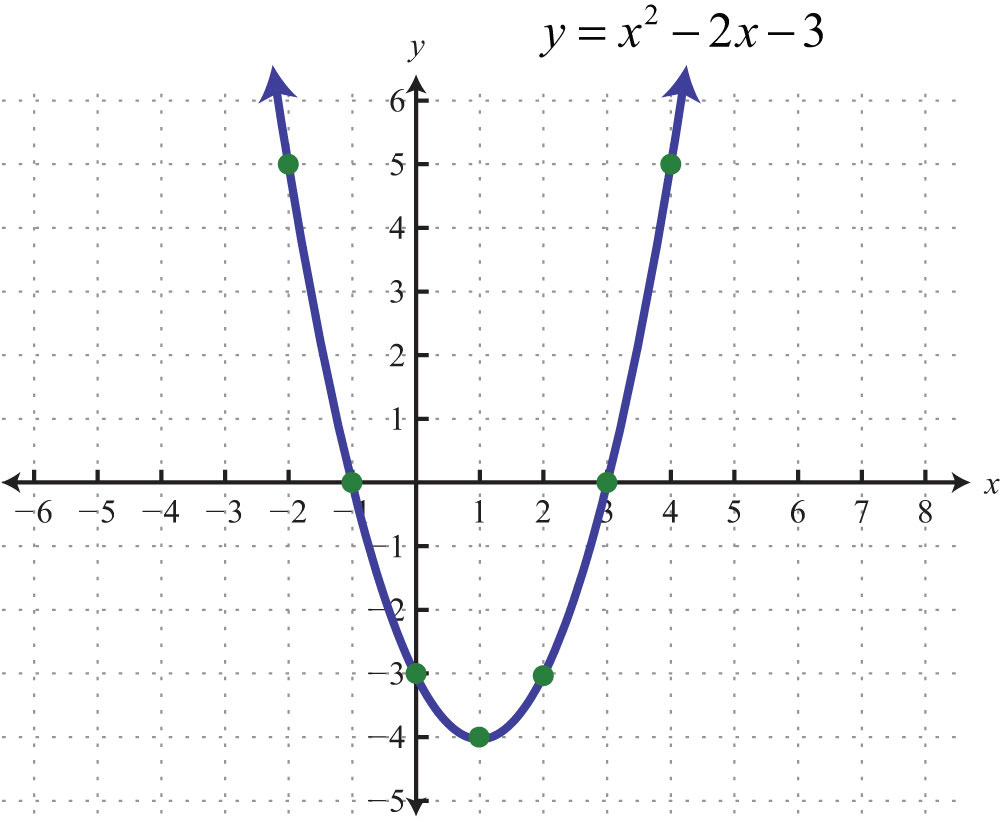
Квадратичная функция вида: \[y=a x^{2}+b x+c\] очень часто используется для того, чтобы задать значения параболы.
Вершина такой функции, всегда находится в произвольной точке.
В технических науках не существует единой формулы, чтобы вычислить сразу две вершины параболы. Однако, довольно легко определяются координаты вершины, по уже упомянутому уравнению.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Алгоритм решения задач по определению точек вершин параболы
- Необходимо выписать коэффициенты a, b, c по условию заданного уравнения. При условии, что коэффициент а будет иметь положительное значение, можно сделать вывод: ветви параболы направлены вверх. Следовательно, если значение отрицательное, то ветви будут направлены вниз.
- Вторым действием определяется абсцисса вершины параболы.
(x) по следующей формуле \[x=-\frac{b}{2 a}\], для этого необходимо применить коэффициенты a, b, c из заданного по заданию уравнения. - Найденное значение x нужно подставить в уравнение, решить его, и тем самым будет выполнен окончательный расчет.
- В ответ записать найденные координаты вершин параболы x и y.
Пример решения уравнения параболы
Рассмотрим подробно на примере, решение задач данной категории.
Запишем данное уравнение следующего вида: \[y=x^{2}-5 x+7\].
Воспользуемся алгоритмом решения, и выполним следующие действия:
- Зададим коэффициенты параболы. Они равны следующим значениям: a=1, b=-5, с=7.
- Чтобы вычислить вершину x параболы, нужно известные коэффициенты a=1, b=-5 подставить в формулу: \[x=-\frac{b}{2 a}=\frac{-5}{2}=2,5\].
- Вычисленное значение х, нужно подставить в исходное уравнение: \[y=2,5^{2}-5 \cdot 2,5+7=0,75\]
- Координаты вершины параболы будут равняться следующим значения: (0,75 и 2,5).















