Формула производной от дроби, примеры
Один из важнейших разделов математики – производные. Для их нахождения существуют специальные формулы производных. Для работы с ними необходимо знать основные формулы элементарных функций.
Таблица формул производных
Ниже приведена таблица формул производных элементарных функций.
| \[C^{\prime}=0\] | \[(\ln \ln x)^{\prime}=\frac{1}{x}\] |
| \[x^{\prime}=1\] | \[(\sin \sin x)^{\prime}=\cos \cos x\] |
| \[\left(x^{2}\right)^{\prime}=2 x\] | \[(\cos \cos x)^{\prime}=-\sin \sin x\] |
| \[\left(x^{n}\right)^{\prime}=n * x^{n-1}\] | \[(\operatorname{tg} x)^{\prime}=\frac{1}{\cos ^{2}(x)}\] |
| \[\left(a^{x}\right)^{\prime}=a^{x} * \ln (a)\] | \[(\operatorname{ctg} x)^{\prime}=-\frac{1}{\sin ^{2}(x)}\] |
| \[\left(e^{x}\right)^{\prime}=e^{x}\] | \[(\arcsin \arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}\] |
| \[(x)^{\prime}=\frac{1}{x * \ln (a)}\] | \[\begin{aligned} (\arccos &\arccos x)^{\prime} \ &=-\frac{1}{\sqrt{1-x^{2}}} \end{aligned}\] |
| \[(\operatorname{arctg} x)^{\prime}=\frac{1}{1+x^{2}}\] | \[(\operatorname{arcctg} x)^{\prime}=-\frac{1}{1+x^{2}}\] |
Смысл производной
В математике производная имеет геометрический и физический смыслы.
Допустим, что некоторая функция f(x) задана в интервале (a, b). При этом есть две точки x и x0, которые находятся в указанном интервале. Если значение x будет изменяться, то и f(x) тоже изменится. Изменение аргумента находится из выражения (x – x0). Эта разность обозначается как Δx – приращение аргумента. В таком случае приращением функции будет являться разность между ее значениями в двух точках. Исходя из этого, можно дать определение производной. Ей называется предел отношения приращения функции к приращению аргумента в указанной точке. При этом сам аргумент стремится к нулю.
В математике формулы производных функций записываются так:
Смысл этих формул, а точнее нахождения их значений, может быть описан с точки зрения геометрии и физики.
Геометрический смысл состоит в том, что производная функции в конкретной точке равняется тангенсу угла, который образован осью абсцисс и касательной линией к графику. Пример показан на рисунке ниже.
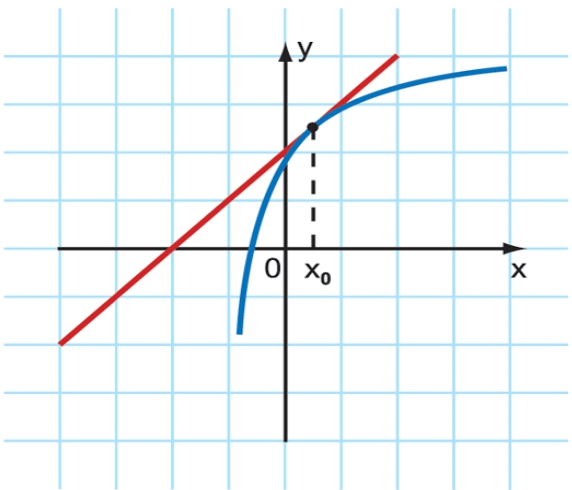
В физике смысл состоит в том, что производная от пройденного расстояния по времени есть скорость движения точки.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Формула вычисления производной дроби
Рассмотрим формулу вычисления производной дроби. Функция v(x) имеет производную в определенной точке x. При этом v(x) не равна нулю (v(x) ≠ 0). В таком случае справедлива следующая формула:
Рассмотрим примеры использования формулы производной дроби при решении задач.
Первый пример с выражениями из тригонометрии: \[y=\frac{\cos \cos x}{x^{2}}\]
Пользуясь таблицей 1 найдем:
\[\begin{gathered}
y^{\prime}=\frac{\left.(\cos \cos x)^{\prime} * (x^{2}-x\right) *\left(x^{2}\right)^{\prime}}{\left(x^{2}\right)^{2}} =\\
\frac{(-\sin \sin x) * x^{2}-(\cos \cos x) * 2 x}{x^{4}} .
\end{gathered}\]
Вынесем x за скобки и преобразуем полученное выражение: \[y^{\prime}=\frac{(-\sin \sin x) * x-2 \cos \cos x}{x^{3}}\]
Другой пример:
\[\begin{gathered}
y=\frac{x^{3}}{x^{3}+2} \\
y^{\prime}=\frac{\left(x^{3}\right)^{\prime} *\left(x^{3}+2\right)-x^{3} *\left(x^{3}+2\right)^{\prime}}{\left(x^{3}+2\right)^{2}} \\
y^{\prime}=\frac{3 x^{2} *\left(x^{3}+2\right)-x^{3} * 3 x^{2}}{\left(x^{3}+2\right)^{2}} \\
y^{\prime}=\frac{3 x^{5}+6 x^{2}-3 x^{5}}{\left(x^{3}+2\right)^{2}}=\frac{6 x^{2}}{\left(x^{3}+2\right)^{2}}
\end{gathered}\]
Решение примеров на нахождение производных в математике называется дифференцированием. Они бывают двух типов:
- частными;
- полными.
Между этими типами есть одно основное отличие. При нахождении частной производной функция аппроксимируется только по одному аргументу. Так во всех предыдущих примерах аппроксимация производилась только по x.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)