Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)
Определение значения площади фигуры, ограниченной линиями y=f(x), x=g(y)
При помощи основных формул и значений интегралов, можно определить площадь криволинейной трапеции G. Для этого используются следующий перечень формул:
Формула, для определения непрерывной и положительной функции, следующего вида: y=f(x) на промежутке [a;b].
Для непрерывной и функции с отрицательными показателями, вида: y=f(x) на числовом промежутке [a;b].
Однако, когда необходимо решить задачи с определением площади фигур, очень часто возникает необходимость применять более сложные фигуры.
Для этого используют фигуры, площади которых ограничены линиями, которые представлены в виде функций следующего типа: как y=f(x) или x=g(y).
Доказательство данных функций подробно описывается для трех случаев, параллельно изображая весь процесс решения графиками на координатной прямой.
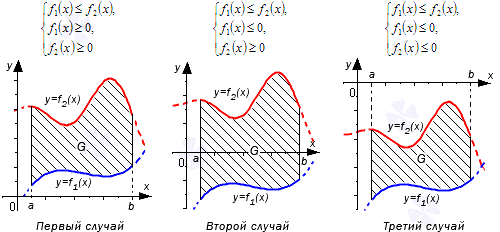
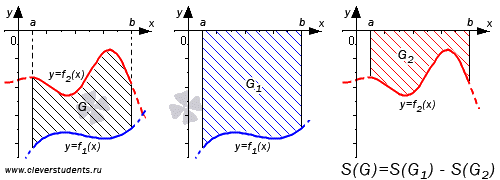
Первый вариант:
В данной ситуации, обе функции имеют положительные характеристики, в силу свойства целостности площади. Следовательно, сумма для площадей исходной фигуры, обозначенной G и криволинейной геометрической трапеции G1 равняется значению площади фигуры G2. Из этого следует:
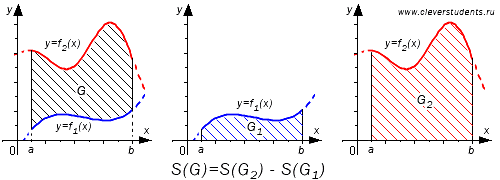
Второй вариант:
Таким же образом, как и в первом случае, можно доказать равенство, которое характерно для второго варианта.
Графически данная ситуация будет выглядеть следующим образом.
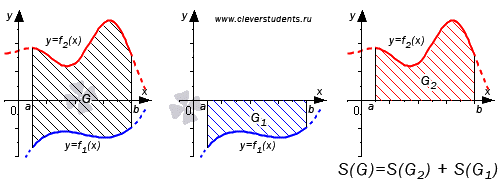
Третий вариант:
Для данного варианта характерно две функции, отрицательные по своим значениям.
Формула, которая применяется для доказательства, выглядит следующим образом:
Для более понятно и доступного восприятия, лучше всего данное доказательство изображать в виде графического рисунка.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
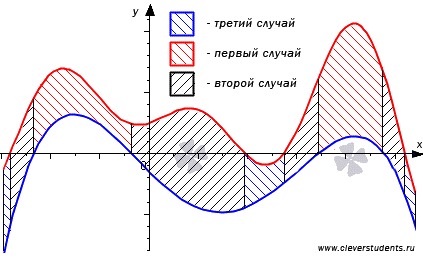
Общий случай, для определения площади фигуры
Общий случай для фигуры, когда функция имеет вид: \[y=f_{1}(x) \text{ и } y=f{2}(x)\] и пересекают ось значений на координатной прямой.
Точки, которые пересекают вышеуказанные функции, можно обозначать следующими показателями: \[x_{i}, \quad i=1,2, \ldots, n-1\]. Данные точки, разделяют промежуток значений (a и b) на несколько частей, которые можно обозначить как n. Значение а всегда равняется b. Заданную фигуру, площадь которой нужно определить, можно обозначить как объединение двух фигур. На интервале, где располагается геометрическая фигура, она попадает под один из трех вариантов, которые были рассмотрены ранее.
Следовательно, можно составить и записать следующее выражение:
Для последнего перехода функции справедливо пятое свойство интегральных значений.
Из этого следует, что заданная формула: \[S(G)=\int_{a}^{b}\left(f_{2}(x)-f_{1}(x)\right) d x\] является доказанной.
Примеры вычисления площади стороны фигуры
Необходимо определить вычислить площадь фигуры ограниченной линиями геометрической фигуры, которая ограничена параболой:
\[y=-x^{2}+6 x-5\] и прямыми линиями: \[y=-\frac{1}{3} x-\frac{1}{2}\], \[, x=1, x=4\].
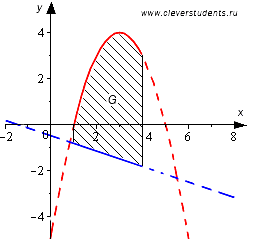
На протяжении всего отрезка [1;4] график в виде параболы равен функции:
\[y=-x^{2}+6 x-5\] и расположен выше прямой: \[y=-\frac{1}{3} x-\frac{1}{2}\]
Следователь, применяя все известные формула и используя алгоритм решения, для определения площади фигуры. Можно определить значение определенного интеграла по формуле Ньютона-Лейбница:
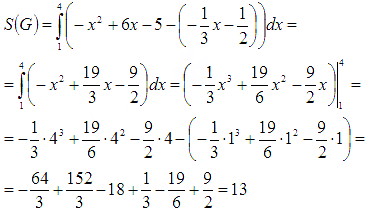
Определим значение площади фигуры, которая ограничена линиями, со следующими значениями:
Для вычисления необходимо выяснить предел интегрирования. Так как дана только одна прямая равная 7.
Для этого необходимо построить график, со всеми известными данными.
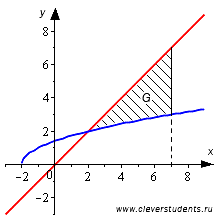
Согласно графику, можно сделать вывод, что нижний предел интегрирования, для определения площади, будет являться точка пересечения графика прямой
y=x и значения половины параболы \[y=\sqrt{x+2}\]
Значение данной точки можно вычислить из следующего равенства:
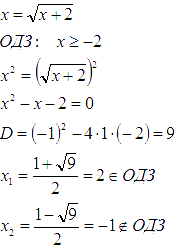
Исходя из вычислений, приведенных выше, можно сделать вывод, что абсциссой точки, где происходит пересечение, будет являться значение 2.
В данном примере и графике видно, что все линии пересекаются в точках на промежутке (2;2).
График функции y=x располагается выше графической функции \[y=\sqrt{x+2}\], которой характерен интервал (2;7).
Для определения площади используем формулу: