Площадь прямоугольной трапеции

Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).

5 способов вычисления:

1. через три стороны трапеции;
2. умножив высоту трапеции на среднюю линию;
3. через основание и углы;
4. через диагонали и углы между ними;
5. через четыре стороны.

Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.

Площадь прямоугольной трапеции по трём сторонам

Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.

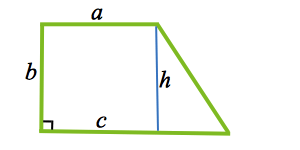
a – малое основание;

b – перпендикулярная сторона;

c – большое основание;

h – высота.

Рисунок 1. Прямоугольная трапеция. Высота h.

 \[\boldsymbol{S}=\frac{\mathbf{1}}{\mathbf{2}} *(\boldsymbol{a}+\boldsymbol{c}) * \boldsymbol{b}, \text { где } \mathbf{S}\], где S – площадь прямоугольной трапеции.

Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.

Задача.

Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.

Решение:

Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.

Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.

Площадь прямоугольной трапеции по высоте и средней линии

Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.

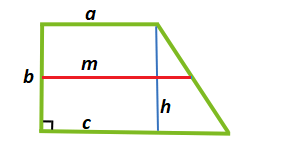
\[\boldsymbol{S}=\boldsymbol{m} * \boldsymbol{h}\], где S – площадь фигуры, m – средняя линия, а h – высота, которую можно заменять на перпендикулярную основаниям сторонуb.

Задача.

Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.

Решение:

Найдём площадь трапеции путём умножения известных величин.

Ответ: S = 29,51 кв.см.

Вычисление площади по основаниям и углам

Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.

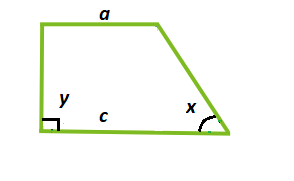
\[S=\frac{1}{2} *\left(c^{2}-a^{2}\right) * \frac{\sin (y) * \sin (x)}{\sin (y+x)}\], где S – площадь; с – большое основание;a – малое основание;

y, x – первый и второй угол при основании.

Задача.

Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8^о?

Решение:

Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.

Ответ: S = 29.48 кв.см.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Площадь прямоугольной трапеции через диагонали и углы между ними

Умножив синус угла, образованный на пересечении диагоналей, на произведение диагоналей, делённое пополам, получим площадь прямоугольной трапеции.

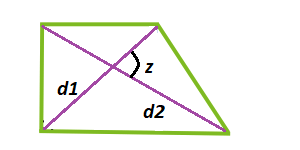
\[S=\frac{1}{2} * d 1 * d 2 * \sin (x)\], где S – площадь; d1 – диагональ 1; d2 – диагональ 2; z – угол между диагоналями.

Задача.

Найдите площадь прямоугольной трапеции, имя данные первой диагонали d1, второй – d2 и угла между ними z. d1 = 2,23 см; d2 = 2,65 см, z = 57^o.

Решение:

Пользуясь формулой расчёта площади, при известных диагоналях и углу между ними, составим решение.

Ответ: S=2,48 кв.см

Площадь прямоугольной трапеции, исходя из значения всех её сторон

Если известны показатели всех сторон прямоугольной трапеции, то вычислить её площадь можно по формуле, приведённой ниже.

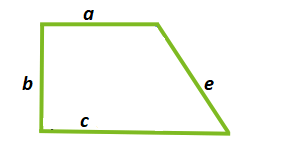
\[\left.S=\frac{a+c}{2} * \sqrt{e^{2}-\left(\frac{(c-a)^{2}+e^{2}-b^{2}}{2 *(c-a)}\right.}\right)^{2}\], где a – малое основание; c – большое основание; b – перпендикулярная основаниям сторона; e – неперпендикулярная боковая сторона.

Задача.

Дано: a = 3 см; b = 3 см; c = 5 см; e = 3,5 см.

Найти: площадь трапеции S.

Решение: применяя формулу расчёта площади по всем сторонам фигуры, найдём площадь трапеции.

Ответ: S = 11,98 кв.см.