Центральная симметрия
Понятие движения, основные правила и определения
Для того чтобы вывести основное определение движения в пространстве, необходимо составить определение отображения пространства на себя.
Отображение пространства — это соответствие каждой любой точке, изучаемого пространства какой-либо заданной точке этого же пространства, в котором задействованы все точки пространства.
Пространственное движение — это отображением пространства на себя, которое фиксирует заданные расстояния между определенными точками.
В ходе движения любой отрезок будет отображаться, как равный ему по параметрам.
Аналогичным образом будет отображаться и другие геометрические фигуры. К таким можно отнести: треугольник, пирамида, квадрат и другие.
Понятие и признаки центральной симметрии
Чтобы правильно составить определение центральной симметрии, необходимо вывести понятие симметричности контурных параметров точек относительно друг друга в зависимости от расположения.
Следовательно, точки х и х1 будут называться симметричными относительно заданной координаты О, в том случае, если знание О будет являться центром отрезка (х и х1).
Центральной симметрией фигуры относительно любой точки будет являться изображение, которое выглядит как фигура, составленная из точек. В свою очередь эти точки симметричны относительно заданной координаты начальной фигуры.
Выполним доказательство данного утверждения. Рассмотрим следующий пример.
Допустим нам даны две точки: z и z” — они будут являться симметричными относительно координаты О. Далее необходимо построить систему координат Ozxy. В полученной системе координат ее центром будет являться точка О. Значения точки z будут следующие координаты \[(\alpha \beta \gamma)\]. Следовательно, точка z’ примет значения \[\left(\alpha^{\prime} \beta^{\prime} \gamma\right)\].
Также стоит отметить тот факт, что все эти точки будут симметричны относительно начала координат.
Для большей наглядности составим и запишем следующее выражение:
\[\begin{aligned}&\frac{\alpha+\alpha^{\prime}}{2}=0; \\&\frac{\beta+\beta^{\prime}}{2}=0; \\&\frac{\gamma+\gamma^{\prime}}{2}=0.\end{aligned}\]
Из этого следует, что: \[\alpha=-\alpha^{\prime}, \beta=-\beta^{\prime}, \gamma=-\gamma^{\prime}\].
Рассмотрим две произвольно заданные значения x и y, с соответствующими координатами \[(\alpha 1 \beta 1 \gamma 1)\] и \[(\alpha 2 \beta 2 \gamma 2)\].
Составим формулу для определения расстояния между координатами:
\[d=\sqrt{\left(a_{1}-a_{2}\right)^{2}+\left(\beta_{1}-\beta_{2}\right)^{2}+\left(\gamma_{1}-\gamma_{2}\right)^{2}}\]
Исходя из вышеизложенной формулы, можно сделать вывод что: параметры x’ и y’ с координатами \[\left(-a_{1},-\beta_{1},-\gamma_{1}\right)\] и \[\left(-a_{2},-\beta_{2},-\gamma_{2}\right)\] соответственно.
Следовательно, расстояние между заданными координатами значений будет определять по следующей формуле:
\[\begin{aligned}&a^{\prime}=\sqrt{\left(-a_{1}-a_{2}\right)^{2}+\left(-\beta_{1}-\beta_{2}\right)^{2}+\left(-\gamma_{1}-\gamma_{2}\right)^{2}}= \\&=\sqrt{\left(a_{1}-_{2}\right)^{2}+\left(\beta_{1}-\beta_{2}\right)^{2}+\left(\gamma_{1}-\gamma_{2}\right)^{2}}=d\end{aligned}\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример решения задач по симметрии точек
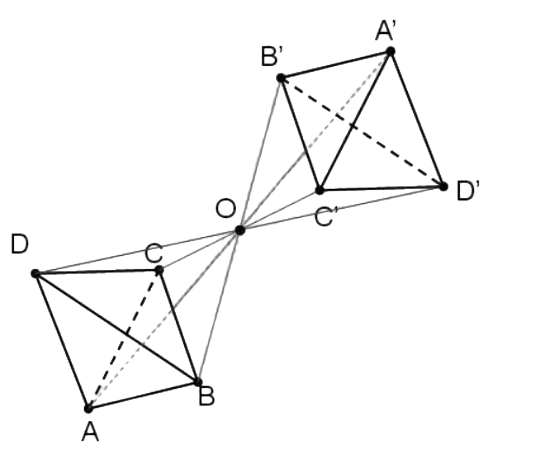
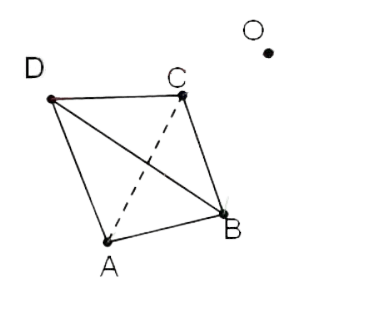
По условию задачи необходимо выполнить построение симметрии центральной симметрии тетраэдра относительно заданных значений и центральной координаты О.
Построение центральной симметрии тетраэдра, относительно точки О, будет выполнено исходя из изображения, которое отражено на рисунке 2.
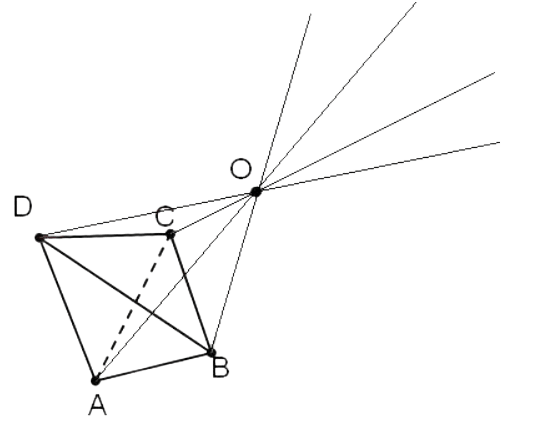
Чтобы выполнить построение центральной симметрии, необходимо для начала провести через все точки геометрической фигуры прямые. Каждая прямая должна проходить через точку О.
Выполнив все необходимые действия получим следующий вид, изображенный на рисунке 3.
Далее, для выполнения следующих этапов решения необходимо воспользоваться уже изученными определениями. Следовательно, точка А переходит в определенную координату равную А’ , которая будет принадлежать заданной прямой ОА. Аналогичная ситуация будет складываться и с остальными точками. Значение В перейдет в такую точку В’ , которая также будет принадлежать прямой (ВО). Точка С преобразовывается в координату С’, которая будет принадлежать прямой (CО). Аналогично, и точка D перейдет в такую точку D’ , которая будет принадлежать прямой DO.
Следовательно, будут выполняться следующие равенства:
\[|A O|=\left|A^{\prime} O\right|,|B O|=\left|B^{\prime} O\right|,|C O|=\left|C^{\prime} O\right|,|D O|=\left|D^{\prime} O\right|\]
Таким образом, центральная симметрия этого тетраэдра изображена на рисунке 4.