Расстояние от точки до прямой на плоскости и в пространстве
Представим некоторую прямую N и точку C, которая не принадлежит этой прямой. Опустим прямую из некоторой точки С к прямой N с пресечением под прямым углом в точке F. Получится отрезок CF, который будет называться наименьшим расстоянием от заданной точки C до рассматриваемой прямой N.
Расстояние от точки до прямой
Данное расстояние эквивалентно длине перпендикуляра, проложенного из рассматриваемой точки к заданной прямой.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
На конкретных примерах нахождение расстояния между точкой и прямой заключается в вычислении высоты той или иной соответствующей фигуры – треугольника, а также параллелограмма или трапеции.
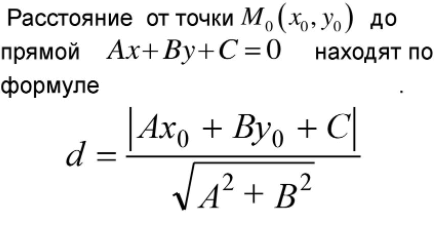
Например: из точки A опущены две наклонные линии к прямой a, отношение длин которых 2:3. Найти расстояние от точки до прямой, когда длина одной проекции равна 2 см, а второй 7 см.
Дано: A∉a
AB⊥a
Наклонные AC и AD, AC:AD=2:3
Проекции этих наклонных BC = 2см и BD = 7 см
Требуется найти: AB
Решение: Считаем k – коэффициент пропорциональности. При этом BC = 2k см и BD = 3k см.
Исследуем прямоугольный треугольник ABC.
В соответствии с теоремой Пифагора получается AC2, = AC2 -BC2 откуда вычисляем:
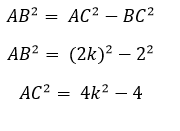
Аналогично для треугольника ACB:
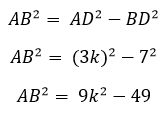
Найдём k, приравняв правые части полученных равенств решим уравнение:
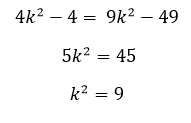
k=3, найдём AB, зная k:
Ответ: ближайшее расстояние от точки до прямой:
Расстояние между двумя точками на прямой
Равняется длине отрезка, который в заданном масштабе соединяет эти точки. Задачу измерения расстояния между соседними точками на прямой в основном рассматривают на координатной прямой, на плоскости в прямоугольной координатной системе, в трёхмерном пространстве,
На координатной прямой расстояние между двумя точками соответствует модулю разности координат конкретных точек.
Если даны точка A(x) и точка B(y), то расстояние между ними d можно вычислить по формуле d=ꟾy-xꟾ. При этом, выражение ꟾy-xꟾ можно заменить выражением ꟾx-yꟾ, полученные значения будут противоположными и их модули равны.
Пример. Даны точки A(2) и B(-6), определить расстояние между точками по прямой.
Решение. Подставим в формулы наши значения, вместо x=2 и y=-6. Следовательно
AB=ꟾy-xꟾ=ꟾ-6-2ꟾ=ꟾ-8ꟾ=8
Ответ: расстояние от точки до прямой равно 8.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Расстояние между точкой и прямой на плоскости
Это наименьшее расстояние от конкретной точки до прямой. Равняется длине перпендикулярного прямой отрезка, соединяющего заданную точку и прямую.
Проложим перпендикуляры на координатной оси из точек A и B. Сделаем анализ прямоугольного треугольника ABC. Имеющего катеты равные:
Для вычислений применим теорему Пифагора, определим длину отрезка AB
Формула для расчёта расстояния от точки до прямой на плоскости: подставим в формулу длины имеющихся отрезков AC и BC с координатами тачек A и B. Аналогично находим расстояние между двумя точками в пространстве.
Пример. Необходимо определить расстояние между точкой A(-1,3) и точкой B(6,2).
Решение:
Ответ: \[\mathrm{AB}=5 \sqrt{2}\]















