Угол между двумя пересекающимися плоскостями
Диагональным называют двугранный угол, образованный двумя полуплоскостями и прямой линией, являющейся их общей границей.
Чтобы находить угол между пересекающимися плоскостями, необходимо понимать основные значения специальных терминов и понятий, которые используются в теме плоскостей и прямых.
Сначала дадим определение того, что называется углом между пересекающимися плоскостями. Если в пространстве две плоскости пересекаются, то между ними образуется угол.
Угол между пересекающейся прямой и плоскостью
Если в пространстве имеются пересекающиеся плоскости Y1 и Y2, то точку пересечения обозначим буквой С. Для построения некой плоскости Х, необходимо рассмотреть заданные пересекающиеся плоскости подробнее.
Новая плоскость Х будет образована вследствие пересечения плоскостей Y1 и Y2. Примем обозначение для прямой, которая будет пересекать Y1 и Х, как прямая а. А другую прямую, которая пересечет Y2 и Х, обозначим как b.
Получаем две пересекающиеся прямые, а и b, которые дадут нам точку M.
Понять, что называется углом между двумя пересекающимися плоскостями, поможет рисунок.
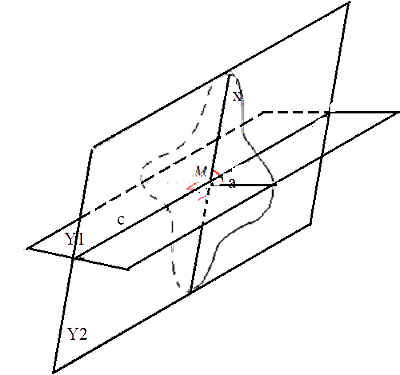
Место расположения точки М не может повлиять на величину угла между a и b, но если М находится на прямой С, то она проходит через плоскость Х.
Для более ясного представления того, что означает угол между двумя пересекающимися плоскостями, нужно:
- Построить перпендикулярную прямую к прямой С, а также лежащую на плоскости Х1.
- При пересечении плоскости Y1 с Y2 и прямой Х1 получаем прямые а1 и b.
- Если при Х и Х1, прямые, а и b перпендикулярны к прямой С, то прямые а1 и b1 также будут перпендикулярны прямой С.
- Построение прямых a и а1, лежащих на плоскости Y1, будет считаться параллельным.
- Прямые b и b1 принадлежат плоскости Y2, имеющей перпендикуляр, то они параллельны.
Как найти угол между двумя пересекающимися плоскостями
Чтобы найти значение, чему равен угол между пересекающимися плоскостями, необходимо сделать дополнительные построения:
- Перенести параллельно плоскость Х1 на плоскость Х.
- Получить совпадающие прямые a и а1, b и b1.
Дадим определение угла между двумя плоскостями.
Угол между прямыми a1 и b1 будет равен углу между пересекающимися прямыми a и b.
Это определение хорошо видно на рисунке.
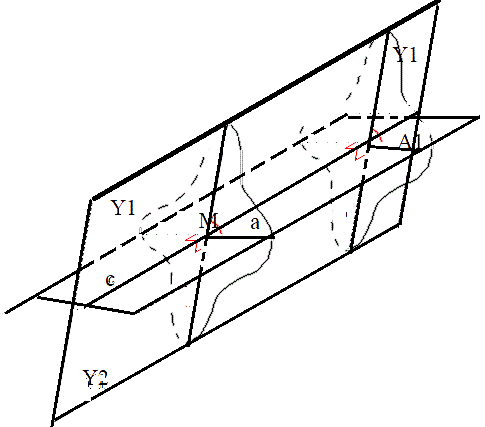
Доказательство:
- Если между прямыми a и b, которые пересекаются, имеем угол между пересекающейся прямой и плоскости, то он не будет зависеть от точки пересечение М.
- Данные прямые принадлежат плоскостям Y1 и Y1, поэтому готовый угол и является углом между пересекающимися плоскостями.
Итак, между двумя плоскостями, которые пересекаются между собой и имеют принадлежащие им прямые линии, в точке третьей плоскости пересечения Х образуется угол, перпендикулярный прямой С.
Чтобы понять это определение, обратимся к рисунку.
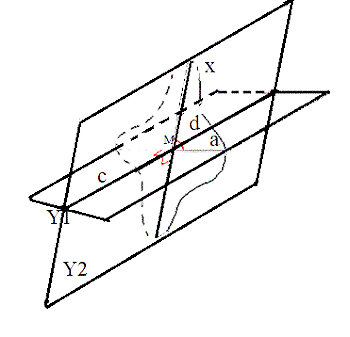
Данное понятие можно сформулировать иначе:
- При пересечении Y1 и Y2 получаем прямую с точкой М.
- Проводим прямые a и b в данных плоскостях, которые будут перпендикулярны прямой c.
- Полученный между двумя прямыми угол будет называться углом между плоскостями.
Этот метод применяют и для построения заданного угла между двумя плоскостями.
Для этого нужно знать следующие правила:
- Угол между плоскостями всегда меньше 900 С.
- Плоскости являются перпендикулярными только в том случае, если угол между ними прямой.
- Между двумя параллельными плоскостями угол равен 0 градусов С.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Методы вычисления угла между плоскостями
Существует несколько методов, позволяющих вычислить угол с максимальной точностью.
Вычислить угол можно несколькими способами:
- используя признаки равенства;
- с помощью треугольников;
- применяя синусы и косинусы;
- используя систему координат.
Необходимо понимать, как найти угол между пересекающимися плоскостями, применяя различные методы. Тогда решение любой задачи покажется легким для выполнения.
Дан один параллелепипед \[A B C D A_{1} B_{1} C_{1} D_{1}\].
Сторона \[A D=3, A B=2, A A_{1}=7\].
Точка E делит сторону \[АА_{1}\] в пропорции 4 : 3.
Задание: необходимо найти угол между плоскостями АВС и \[ВED_{1}\].
Решение:
Сначала сделаем чертеж исходного задания.
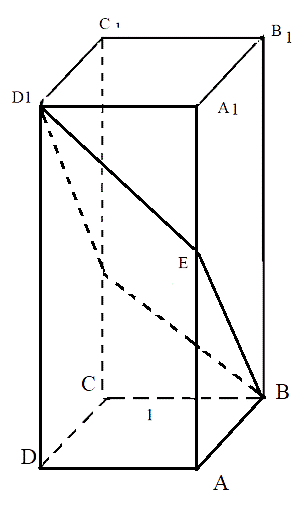
Теперь необходимо обозначить прямую линию пересечения двух плоскостей АВС и \[ВED_{1}\].
Точка B будет общей, далее необходимо найти еще одну точку пересечения.
Поскольку прямые DA и \[D_{1}E\] располагаются в плоскости \[ADD_{1}\] и не могут быть параллельны, значит они пересекаются.
Если прямая DA расположена в плоскости АВС, а \[D_{1}E\] в BED1, то прямые DA и D1E однозначно пересекаются в общей точке, которая лежит на обеих плоскостях. Обозначим эту точку буквой F.
На рисунке хорошо видно, что прямая BF является общей для двух исходных плоскостей.
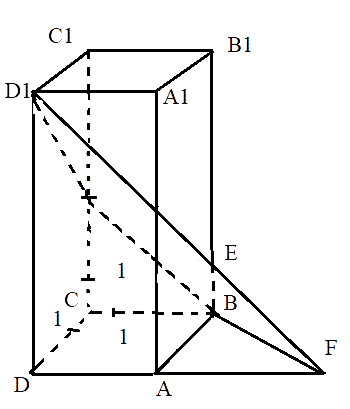
Теперь постараемся найти угол между этими плоскостями:
- Построим прямые в обеих плоскостях, проходящие через общую точку, лежащую на прямой BF и
перпендикулярные ей. - Получился угол между плоскостями.
- Точка А, лежащая на плоскости АВС, является проекцией точки Е.
- Проводим перпендикулярную прямую к BF в точке М.
- Теперь хорошо видно, что ЕМ является проекцией на плоскость АВС в АМ.
- Применяем теорему о перпендикулярах AM ⊥ BF.
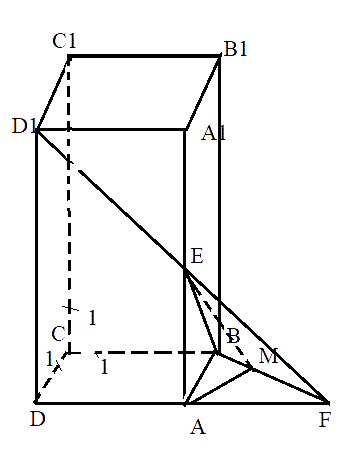
Искомым является ∠AME, который образован пересечением плоскостей АВС и \[ВED_{1}\]. Из полученного треугольника АЕМ находим тангенс, синус или косинус. Теперь, если известны стороны треугольника, можно вычислить угол между двумя пересекающимися плоскостями.
Для этого выполняем несколько дополнительных действий:
В условии задачи сказано, что АА1 разделена точкой Е в пропорции 4 : 3. Это значит, что прямая имеет 7 частей, а отрезок АЕ равен 4 частям.
Чтобы определить АМ, нужно рассмотреть треугольник АВF, где угол A прямой, а АМ является его высотой.
Если АВ = 2, то длину AF можно вычислить по принципу подобия треугольников DD1F и AEF:
\[\frac{A E}{D D 1}=\frac{A F}{D F} \Leftrightarrow \frac{A E}{D D 1}=\frac{A F}{D A+A F} \Rightarrow
\frac{4}{7}=\frac{A F}{3+A F} \Leftrightarrow A F=4\]
С помощью теоремы Пифагора находим длину BF в треугольнике ABF:
\[\mathrm{BF}=\sqrt{(}\left(\mathrm{AB}^{2}+\mathrm{AF}^{2}\right)=\sqrt{\left(2^{2}+4^{2}\right)}=2
\sqrt{5}\]
Находим длину отрезка АМ через площадь треугольника ABF:
S треугольника \[\mathrm{ABC}=\frac{1}{2} \cdot \mathrm{AB} \cdot \mathrm{AF}\] или S треугольника
\[\mathrm{ABC}=\frac{1}{2} \cdot \mathrm{BF} \cdot AM\]. Тогда \[\mathrm{AM}=\frac{A B \cdot A F}{B
F}=\frac{2 \cdot 4}{2 \sqrt{5}}=\frac{4 \sqrt{5}}{5}\].
Находим тангенс угла в треугольнике АЕМ:
\[\operatorname{tg} \angle \mathrm{AME}=\frac{A E}{A M}=\frac{4}{4 \sqrt{5}}: 5=\sqrt{5}\]
В итоге угол между пересекающимися плоскостями arc равен arctg√5. Или \[\operatorname{arctg} \sqrt{5}=\arcsin
\frac{\sqrt{30}}{6}=\arccos \frac{\sqrt{6}}{6}\].
Ответ: \[\operatorname{arctg} \sqrt{5}=\arccos \frac{\sqrt{6}}{6}\].
B единичном кубе \[A B C D A_{1} B_{1} C_{1} D_{1}\] найдите угол между плоскостями \[\left(A D_{1}
E\right)\] и \[\left(D_{1} F C\right)\], где точки E и F — середины ребер \[A_{1} B_{1}\] и \[B_{1} C_{1}\] соответственно.
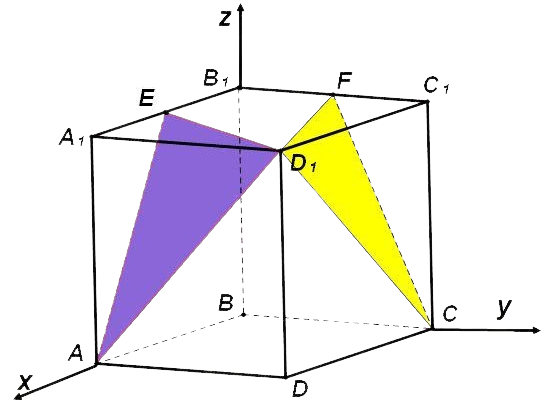
Решение:
Введем прямоугольную систему координат и определим координаты точек:\[A(1 ; 0 ; 0), C(0 ;
1 ; 0), D_{1}(1 ; 1 ; 1), E\left(\frac{1}{2} ; 0 ; 1\right), F\left(0 ; \frac{1}{2} ; 1\right)\]
Составим уравнение плоскости \[\left(A D_{1} E\right)\]:
\[2 x-y+z-2=0\\\overrightarrow{n_{1}}\{2 ;-1 ;
1\}\] — нормальный вектор плоскости \[(AD_{1} E)\].
Составим уравнение плоскости \[\left(D_{1} F C\right)\]:
\[x-2 y-z+2=0\\\overrightarrow{n_{2}}\{1 ;-2
;-1\}\] — нормальный вектор плоскости \[(D_{1}FC)\].
Отрезок, соединяющий центр основания правильной треугольной пирамиды с серединой бокового ребра,
равен стороне основания. Найти угол между смежными боковыми гранями пирамиды.
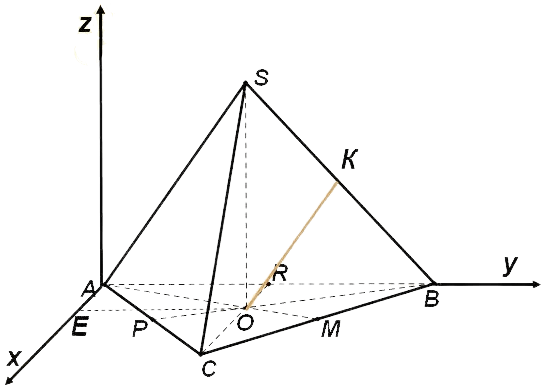
Решение: \[R O=\frac{1}{3}; C R=\frac{\sqrt{3}}{6}; E O=\frac{1}{2}\]
SO найдем из \[\triangle O S B\]:
\[\begin{aligned}&S B=2, \quad B O=\frac{\sqrt{3}}{3} \\&S O=\sqrt{S B^{2}-O B^{2}} \\&S
O=\sqrt{4-\frac{1}{3}}=\frac{\sqrt{11}}{\sqrt{3}} \\&S\left(\frac{\sqrt{3}}{6} ; \frac{1}{2} ;
\frac{\sqrt{11}}{\sqrt{3}}\right)\end{aligned}\]















