Линейные неравенства, примеры, решения
В статье мы рассмотрим, что собой представляют линейные неравенства с одной переменной и покажем, какими способами их можно решать.
Понятие линейного неравенства
Линейными неравенствами с одной переменной называются неравенства, которые можно записать в виде формулы ax + b > 0. Вместо «>» могут быть знаки «<» или «≤», «≥». x – неизвестная переменная. a и b – действительные числа.
Линейными неравенствами с одной переменной называют неравенства a*x < c либо a*x > c, в которых x – искомая переменная, а a и c некоторые числа. О том, что коэффициент при x может или не может быть равным нулю, ничего не говорится. Это позволяет строгое неравенство 0*x > c и 0*x < c записать в виде 0*x ≥ c и 0*x ≤ c.
Линейными неравенствами с одной переменой считают неравенства, имеющие вид ax + b < 0, ax + b > 0, ax + b ≥ 0, ax + b ≤ 0. Где a и b являются любыми числами, но a не должно равняться нулю. x – искомая переменная.
Неравенства ax + b > 0 и ax > c считаются равносильными, так как получаются с помощью переноса слагаемого из одной их части в другую. Решения подобных неравенств совпадают.
Примеры линейных неравенств с одной переменной:
- -2x + 4 > 0;
- 3x +1 ≤ 0;
- 2(x-1) < 2x-4;
- 3x+1 ≤ 6-3x
- 3x – 6 > 0.
Как решать линейные неравенства
Решением линейного неравенства называют нахождение всех значений переменной x, при которых оно сохраняет свою силу. Самыми распространёнными и результативными способами, с помощью которых удаётся решить подавляющее большинство линейных неравенств являются метод равносильных преобразований, метод интервалов и графический метод. Рассмотрим каждый из них подробнее.
Решение линейных неравенств с помощью равносильных преобразований
Применительно к нашему случаю равносильными называются следующие преобразования:
- Перенос одного и более членов неравенства из одной части в другую. При этом знак переносимого слагаемого меняется на противоположный. В качестве примеров подобного рода неравенств можно привести
2x − 3 > 6 и 2x > 6 + 3 или 10x – 1 > 3 и 10x > 3 + 1.
- Деление или умножение обеих частей неравенства на одно положительное число. Знак неравенства при этом остаётся тем же. В качестве примеров можно указать
2x > 9 и 10x > 45 или -9x > -15 и -3x > -5.
- Деление или умножение обеих частей неравенства на одно отрицательное число. Знак неравенства при этом нужно сменить на противоположный. Примеры подобных неравенств следующие 5x < -8 и -10x>16 или 9x +12 > 21 и 3x — 4 < -7.
Решить: 2x – 9 >3.
Решение: Видно, что коэффициент при x ненулевой. Это значит, описанные выше преобразования применимы.
Переносим свободное слагаемое из левой части в правую и получаем 2x > 3+9, 2x > 12
Разделим обе части на 2. Будем иметь x > 6. Это неравенство равносильно 2x – 9 >3.
Полученное решение можно записать в виде x > 6 либо \[(6,+\infty)\].
Скобки круглые т. к. неравенство строгое.
Ответ: \[(6,+\infty)\].
Решить: -5x – 8 ≥ 12
Решение: Коэффициент при x равен -5 т. е. тоже не нулевой, а значит можно решать дальше. Переносим -8 в правую часть и получаем -5x ≥ 12 + 8, -5x ≥ 20.
Делим обе части на -5. Не забываем, что при этом необходимо будет сменить знак.
x ≤ -4
Решение записываем, как x ≤ -4 или (-∞, -4]. Скобка в конце стоит квадратная т. к. x может быть не только меньше, но и равным 4.
Ответ: (-∞, -4].
Если числовое неравенство b > 0 («<», «≤», «≥») верно, то исходное неравенство будет иметь своё решение при любом из значений x. Если же оно неверно, то у исходного неравенства решений нет вовсе.
Решить неравенство: 0*x + 9 > 0.
Решение: Указанное неравенство равносильно 9 > 0.
x при этом может принимать совершенно любые значения.
Решение имеет вид (-∞, ∞).
Ответ: (-∞, ∞).
Решить: 0*x + 3 < 0.
Решение: Данное неравенство сводится к 3 < 0
Оно является неверным, а значит неравенство решений не имеет.
Ответ: решений нет.
У некоторых из читателей возможно появился вопрос, как быть, если и в роли коэффициента при x, и в роли слагаемого выступает ноль. Это неравенства 0*x + 0 < 0, 0*x + 0 > 0, 0*x + 0 ≤ 0, 0*x + 0 ≥ 0. Два первых из них решений не имеют, ведь ноль не может быть больше или меньше самого себя. У двух последних решения есть т. к. любое число равно самому себе, в частности, ноль равен нулю.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Решение линейных неравенств методом интервалов
Он может быть использован лишь тогда, когда коэффициент при x не равен нулю. Последовательность действий при использовании указанного метода следующая:
- Находятся нули функции y = ax + b. Для этого, нужно решить уравнение ax + b = 0. При a неравном нулю его решение будет состоять из одного корня x0.
- Строится координатная прямая. На ней изображается точка с координатой x0. При строгом неравенстве точку нужно изобразить выколотой. При нестрогом – закрашенной.
- На промежутках определяются знаки функции y = ax + b. Если решение неравенства имеет знаки > или ≥, то добавляется штриховка над положительным промежутком. Если решение идёт со знаками если < или ≤, штриховка происходит над отрицательным промежутком.
Решить: −6x + 12 > 0 методом интервалов.
Решение:
Действуем в соответствии с алгоритмом. Находим корень уравнения − 6x + 12 = 0.
Делим обе части выражения на -6. Получаем x=2.
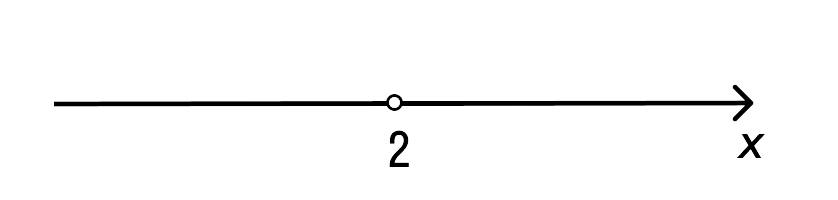
Для определения знака на промежутке (−∞, 2) вычисляем функцию y = −6x + 12 при х = 1. Видим, что −6 * 1 + 12
= 6, 6 > 0, т. е. знак положительный. Определяем, какой знак на промежутке (2, + ∞). Для этого в функцию
подставляем х = 3. Получаем
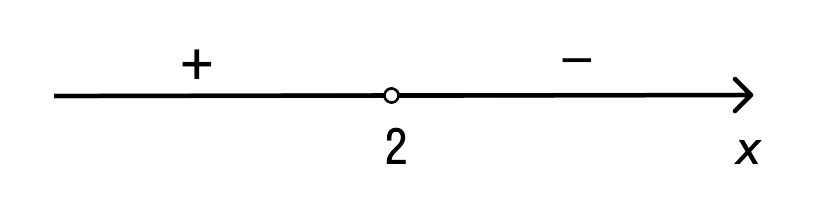
Штрихуем положительный промежуток
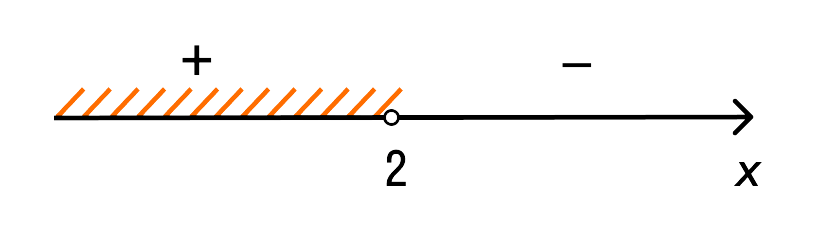
Из чертежа ясно, что решение нашего неравенства (−∞, 2) или x < 2.
Ответ: (−∞, 2).
Решение неравенств графическим способом
Главное при пользовании этим методом правильно найти промежутки, которые требуется изобразить на графике.
Действия при пользовании графическим способом следующие:
- При решении ax + b < 0 определяем промежуток, где график будет ниже оси 0x;
- При решении ax + b ≤ 0 определяем промежуток, где график либо ниже 0х, либо совпадает с ней;
- При решении ax + b > 0 определяем промежуток, где график выше оси 0х;
- При решении ax + b ≥ 0 определяем промежуток, где график выше оси 0х или совпадает с ней.
Решить: −4 * x − √3> 0
Коэффициент при x отрицательный, значит наша прямая убывающая. Чтобы определить точки её пересечения с осью 0x нужно решить уравнение −4 * x − √3 = 0
X= -√3/4
Построим график этого линейного неравенства y=0.
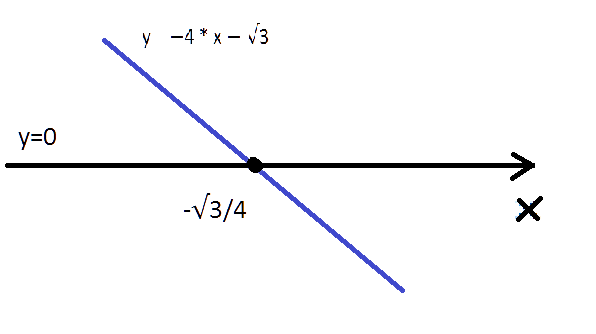
Т. к. у решения неравенства знак >, внимание следует обращать на промежуток выше оси 0x.
Он находится левее точки -√3/4.
Видно, что решением неравенства будет (−∞, −√3/4).
Ответ: (−∞, −√3/ 5).
Неравенства, сводящиеся к линейным
При их решении следует использовать такие приёмы, как раскрытие скобок, собирание в левой части неравенства чисел, а в правой переменных, деление обеих частей на коэффициент при x.
Решить: 3x + 2 > 2(x + 3) + x.
Решение: Раскрываем в правой частях скобки 3x + 2 > 2x + 6 + x.
Переносим члены с иксами в одну сторону, без иксов в другую.
3x — 2x — x > 6 – 2
0x > 4
0 > 4
Получаем противоречие, т. е. неравенство решения не имеет.
Ответ: решений нет.















