Решение кубических уравнений
Кубическим называют уравнение, в котором только одна переменная представлена в третьей степени. Такие выражения в любом случае имеют от одного до трех корней. Значения, которые получаются при решении таких уравнений, могут быть равными друг другу или комплексными, если их не более двух.
Решение кубических уравнений – это решение уравнений, имеющих вид: \[\boldsymbol{a y^{3}+b y^{2}+c y+d=0}\].
В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.
Данный вид уравнения имеет как минимум один корень – y1.
Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:
- разложение на множители;
- применение формул для квадратных уравнений;
- метод дополнения.
Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.
Решение кубических уравнений с двумя членами
Уравнение будет иметь вид: \[\boldsymbol{a y^{3}+b=0}\]
Для решения необходимо преобразовать его: \[y^{3}=b / a=0\]
Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:
y3=b/a=0
(y+3√b/a)(y2—3√b/a*y+3√(b/a)2)=0
В результате из первой скобки выводим:
y=-3√b/a
во второй скобке получаем выражение – трехчлен:
y2-3√b/a*y+3√(b/a)2
Методы решения кубических уравнений возвратного вида
Алгоритм решения кубического уравнения возвратного вида отличается от предыдущего, так как оно выглядит следующим образом:
\[\boldsymbol{a y^{3}+b y^{2}+b y+a=0}\]
В этом уравнении переменные a и b – это коэффициенты.
Первым делом при решении таких уравнений в математике выполняется группировка:
ay3+by2+by+a=a(y3+1)+b(y2+y)=a(y+1)(y2-y+1)+by(y+1)=(y+1)(ay2+y(b-a)+a)
В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay2+y(b-a)+a, потребуется найти дискриминант.
Дискриминант – произведение квадратов разностей корней в различных вариаций.
Решение кубических уравнений в составе которых рациональные корни
Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:
ay3+by2+cy+d=0
При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:
ay3+by2+cy=0
Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:
y(ay2+by+c)=0
Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:
5y3+2y2+4y=0
Решение:
Первым делом стоит упростить уравнение.
5y3+2y2+4y=0
Получим уравнение вида:
y(5y2+2y+4)=0
y=0, так как является корнем выражения.
Следующий шаг – поиск корней квадратного трехчлена 5y2+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.
В ходе решения кубического уравнения с дискриминантом получим:
D=22-2*5*4=-38
Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.
Если в уравнениях вида ay3+by2+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.
В случае, когда a не равно 0, при умножении на a2 каждой составляющей уравнения происходит замещение переменных, и получается: x=ay
ay3+by2+cy+d=0
Каждую составляющую выражения умножаем на a2:
a3*y3+b*a2*y2+c*a*a*y+d*a2=0
Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:
x2+b*x2+c*a*x+d*a2
Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x1 будет корнем, и в то же время корнем начального уравнения:
x1=y1/a
Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y1.
Рассмотрим решение кубических уравнений такого вида на примере.
Пример:
Решить уравнение \[x 3-3 x 2-13 x+15=0\].
Решение:
Ищем первый корень перебором чисел: \[0, \pm1, \pm2, \pm3, \pm5, \pm15\] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:
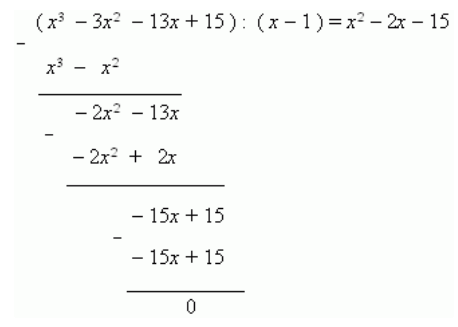
Теперь, решая квадратное уравнение: \[x 2-2 x-15=0\], находим оставшиеся два корня: x1=-3 и x2=5.
Ответ: 1; -3; 5.
Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.
Решение кубического уравнения с помощью формулы Кардано
Есть еще один способ — формула Кардано для решения кубических уравнений.
Если взять уравнение вида B0y3+B1y2+B2y+B3=0, то A1=B1/B0, A2=B2/B0, A3=B3/B0.
Z=-A21/3+A2
P=2A31/27-A1A2/3+A3.
Выведенные значение Z и P подставим в формулу Кардано.
X=3√-P/2+√P2/4+Z3/27+3√-P/2-+√P2/4+Z3/27
В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:
y=x-A1/3
Применить формулу Кордано можно на примере для наглядности.
Решить уравнение \[x^{3}+6 x^{2}+3 x-10=0\]
Решение
Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень \[x=1\]. Делением
\[x=1\] левой части уравнения по схеме Горнера получаем:
\[\begin{array}{r}+\begin{array}{r}1&6&3&-10\\0&1*1=1&7*1=7&10*1=10\\\end{array}
\\\hline\begin{array}{r}1\quad\quad\quad&7\quad\quad\quad&10\quad\quad\quad\quad&0\end{array}\end{array}\]
Следовательно, \[x^{2}+7 x+10=0\]. Решая это квадратное уравнение, получаем
\[x=\frac{-7 \pm \sqrt{7^{2}-4 * 1 * 10}}{2} \Leftrightarrow x_{1}=-2, \quad x_{2}=-5\]
А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения \[a=1, b=6, c=3, d=-10\].
Замена переменной \[x=y-\frac{b}{3 a}=y-\frac{6}{3}=y-2\] приводит исходное уравнение к виду \[y^{3}+p
y+q=0\], где:
\[p=\frac{3 a c-b^{2}}{3 a^{2}}=\frac{3 * 1 * 3-6^{2}}{3 * 1^{2}}=-9, \quad q=\\\frac{2 b^{3}-9 a b c+27 a^{2}
d}{27 a^{3}}=\frac{2 * 6^{3}-9 * 1 * 6 * 3+27 * 1^{2} *(-10)}{27 * 1^{3}}=0\]
Вычислим дискриминант этого уравнения:
\[\Delta=\left(\frac{q}{2}\right)^{2}+\left(\frac{p}{3}\right)^{3}=\left(\frac{0}{2}\right)^{2}+\left(-\frac{9}{3}\right)^{3}=-27\]
Так \[\Delta\] каноническое уравнение имеет 3 действительных корня. Поскольку \[q=0 \Rightarrow
\varphi=\frac{\pi}{2}=>\]
\[y_{1}=2 \sqrt{-\frac{p}{3}} * \cos \left(\frac{\varphi}{3}\right)=2 \sqrt{-\frac{-9}{3}} * \cos
\left(\frac{\frac{\pi}{2}}{3}\right)=2 \sqrt{3} * \cos \left(\frac{\pi}{6}\right)=2 \sqrt{3} *
\frac{\sqrt{3}}{2}=3,\\y_{2}=2 \sqrt{-\frac{p}{3}} * \cos \left(\frac{\varphi}{3}+\frac{2 \pi}{3}\right)=2
\sqrt{3} * \cos \left(\frac{\frac{\pi}{2}}{3}+\frac{2 \pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{5
\pi}{6}\right)=-2 \sqrt{3} * \frac{\sqrt{3}}{2}=-3,\\y_{3}=2 \sqrt{-\frac{p}{3}} * \cos
\left(\frac{\varphi}{3}+\frac{4 \pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{\frac{\pi}{2}}{3}+\frac{4
\pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{3 \pi}{2}\right)=0.\]
В данном случае для корней начального уравнения мы получим:
x1=y1-2=3-2=1;
x2=y2-2=-3-2=-5;
x3=y3-2=0-2=-2.
Получаем ответы: 1, -5, -2.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Общее решение кубического уравнения, если известен один из корней
За исходное уравнение возьмем следующее:
y3+ay2+by+c=0
Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y1. В таком случае, если произвести деление начального уравнения y3+ay2+by+c=0 на y-y1 получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y2 и y3.
Чтобы доказать это, преобразуем кубический многочлен следующим образом:
y3+ay2+by+c=(y-y1)(y-y2)(y-y3)
При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.
Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)