Основные определения и свойства степеней в математике
В предложенном материале мы подробно будем изучать степени, их свойства. И постараемся весь изученный материал усвоить на примерах.
В этой статье мы подробно изучим, что такое степень числа. Разберемся и охарактеризуем определения степени числа. При этом выучим все существующие в математике показатели степени. Начиная от натурального числового показателя, заканчивая рациональным показателем.
Весь материал попутно будем рассматривать, и закреплять на конкретных примерах.
Перед тем, как приступить к изучению основных свойств степеней, разберем следующие основные определения, которые нам понадобятся в процессе всего изучения материала определения:
- основное понятие степени;
- что называют основание степени;
- показатели степени;
- вычисление значений в степень;
- основные свойства степеней.
Степень числового значения — это перемноженные между собой одинаковые значения.
Разберем данное определение на примерах:
2· 2 =4
2· 2· 2=8
2 ·2· 2 ·2· 2 ·2=64
Левую часть равенства можно упростить. Для начала указать множитель, который повторяется, и обозначить количество его повторений. Повторяющийся множитель в данном случае это 2. Дублируется он три и шесть раз соответственно. Поэтому над двойкой записываем 3 и 6:
23=2· 2 ·2
24=2· 2·2·2
26 =2·2·2·2·2·2
28 =2·2·2·2·2·2·2·2
Формулировка выражений звучит следующим образом:
- два в четвертой степени равно шестнадцать;
- два в шестой степени равно шестьдесят четыре;
- два в восьмой степени равно двести пятьдесят шесть;
Основание выражения степени — это числовое или буквенное значение, которое повторяется в выражении не однократно.
В вышеизложенных выражениях — это число два.
Показатель степени — это значение, которое отображает, количество повторений основания степени.
53 =5· 5· 5
63 =6 ·6 ·6
В примере, мы видим, что число 5 и 6 повторяется три раза, так как степень, в которую нужно возвести число равняется трем.
Если степень, будет иметь иное значение. Например: 7, то показатель степени будет равняться семи.
Иными словами, приведенный расчет называется приведением в степень.
Например: нам необходимо определить произведение пяти одинаковых чисел, каждый из них равен 3, то правильно будет сказано, что число 3 возводится в пятую степень:
35=3·3·3·3·3 =243
Видим, что число три в пятой степени равняется числу 243.
Для закрепления разберем еще несколько простых примеров.
Пример 1.
34= 3·3·3·3 =81
Пример 2.
74= 7·7·7·7 =2401
Пример 3
84= 8·8·8·8 =4096
Степени, так же подразделяются на:
— целую степень;
— вещественную степень;
— рациональную степень;
— комплексную степень.
В алгебре, да и, в общем, в математике, степень, как правило, имеет четыре основных свойства:
- натуральную степень показателя значения;
- степень целого показателя;
- рациональную и иррациональную.
В данном уроке, мы поочередно разберемся с каждым свойством, его особенностями расчетов. Закрепим материал на конкретных примерах с применением числовых данных.
Свойство степени с натуральным показателем и особенности вычисления
Натуральный показатель степени и его свойства — это, где показателем степени является натуральное, положительное числовое значение.
Натуральный показатель степени имеет следующие свойства:
а) Главное свойство:
xnxm =xn+m
ynym =xn+m
Равенство является верным при любых значениях m и n. И действительном значении а.
(x x …x) — n множителей
(x x …x) — m множителе
Равенство мы разберем на конкретном числовом примере:
Мы имеем две степени с основание четыре.
Натуральные показатели имеют значения три, и пять соответственно.
Составим равенство, подставляя числовые значения:
43 x45=(4·4·4)(4·4·4·4·4)=64×1024=65536 или 48=4·4·4·4·4·4·4·4=65536
Решив равенство, мы получаем: 4345=48
Тем самым, мы видим, что равенство доказано.
Также, используя свойство умножения, можно обобщить свойства. Если в равенстве представлены от трех и более степеней. Натуральные числа обозначим m1, m2.
Составим равенство: xm1xm2……xmk
Составим несколько равенство, подставляя числовые значения, для лучшего усвоения:
(2)2(2)3(2)3(2)4=(2)2+3+3+4=(2)12
(3)2(3)3(3)3(3)4=(3)2+3+3+4=(3)12
(5)2(5)3(5)3(5)4=(5)2+3+3+4=(5)12
б) Свойство частных степени, когда основания имеют одинаковые значения
Свойство частных имеет следующий вид, в виде равенства:
xnxm =xn-m
Оно справедливо при любых натуральных значений n и m, любом значении x, кроме нуля. Значение основания, нельзя принимать равным нулю. В противном случае при расчете, придется делить на ноль, что по правилам математики недопустимо.
Так же, есть еще одно условие: значение n должно быть больше, значения m. После вычета должно получится положительное число.
Для доказательства условия, составим равенство:
xn-mxm=x(n-m)+m=xn
Преобразовав равенство, мы можем вывести следующий пример:
xn-mxm=xn
Для наглядности, подставим числовые значения:
2522=25-3=23
4542=45-3=42
в) Произведение степеней
Степень произведения можно выразить в виде равенства:
(xy)m=xmym
Равенство можно преобразовать в следующей вид:
(xy)m=(xy)(xy)……(xy), количество множителей равно числовому значению степени.
Рассмотрим несколько равенств с числовыми значениями:
— Вариант для положительных значений:
(45)3=(4)3(5)3
(58)3=(5)3(8)3
— Вариант для дробей:
(56×24)4=(56)4(24)4
— Вариант отрицательных значений:
(56(-89))4=(56)4(-89)4
г) Возведение частного в натуральную степень.
Составим равенство для доказательства данного свойства.
(xy)m=xmym
Должны соблюдаться следующие условия:
- значения x и y, должны быть не равны нулю;
- степень (m) — натуральное число.
Для доказательств равенства распишем пример:
(xy)mym=((xy)y)n=xm
Для закрепления знаний, решим несколько примеров, заменяя буквенные значения числовыми.
(168)2=(16)2(8)2
(12(-7))2=(12)2(-7)2
(1,3(-3))3=(1,3)3(-3)3
(1,4(-3))3=(1,4)3(-3)3
д) Принцип возведения степени в степень
Составим равенство:
(xn)m=xnxm
(25)4=25x4=220
Также, данное свойство, может быть выражено и несколькими степенями, в виде:
((((xn)b)a)m=xn·x·b·a·m
Для решения равенства, такого типа, необходимо перемножить между собой значение степеней.
((((32)3)4)2=32342=348
((((5)3)4)2=52342=548
((((12)3)4)6=32346=3192
е) Принципы равенства и неравенства.
Данный принцип звучит следующим образом: большее значение имеет степень, у которой значение основания степени большее или наоборот.
Например:
x2<y2 или подставив числовые значения, образует вид: 45<55
Еще несколько примеров для закрепления, с разными числовыми значениями:
121,5<32 1.5
42>32
32>12
Как видно из примеров, равенство верно, в том случае если значение основания больше.
Принцип неравенства считается верным, если одна степень больше значения другой, а основание больше нуля, но не меньше единицы. То есть, числовое значение должно быть положительным.
xn>xm
45>42
Степень с целым показателем и ее свойства
После того как мы определили степень числа с натуральным показателем, мы можем дальше продолжать расширять знания о степени и перейти к степени числа, показателем которой является любое число, в том числе и отрицательное и ноль. Из этого следует, чтобы оставались правильными все свойства степени, потому что натуральные числа являются составляющей целых чисел.
Степень с целым показателем — это степень, когда любое целое число, является показателем.
Натуральный вид степени тоже является степенью с целым показателем, потому что натуральные числовые значения так же являются целыми числами.
Для степеней с целыми положительными показателями, свойства аналогичны, как и для натуральных показателей.
Рассмотрим основные свойства степеней с целыми показателями.
- Принцип решения отрицательных степеней.
Рассмотрим следующую последовательность степеней:
3031323334353637
Первая степень в данной цепочке 30. Предыдущая степень с целым показателе будем уже с отрицательным значением 3-1.
3-13031323334353637
Продолжим решать значения с отрицательными степенями:
3-73-63-53-43-33-23-13031323334353637
Теперь определим степени с натуральным значением и с нулем.
Расчеты приведены в таблице 1
Таблицы 1. Расчет степени с натуральными показателями и с нулем
| Значение степени | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Если вычисление положительных значений и нуля, особых трудностей не вызывает. А что делать с отрицательными показателями? На этот вопрос мы ответим далее.
При возведении в положительную степень, как правило, число имеет большее значение. А вот при вычислении в отрицательной степени, результат будет иметь меньшее значение.
Если для примера взять число z, и начать поочередно увеличивать его степень, то в результате мы увидим поочередность чисел, где последующее число меньше следующего в z раз.
Для примера, возьмем число 4.Начало расчета возьмем ноль и будем поочередно повышать степень. Далее найдем значение при вычислении.
Расчеты приведены в таблицу 2.
Таблицы 2. Расчет степени с натуральными показателями.
| Значение степени | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Получили перечень чисел, в котором каждое число больше предыдущего числа в четыре раза. Тогда правильно предположить, что число, которое имеет значение больше единицы, будет в четыре раза больше единицы.
Для определения и решения выражения 4-1 , необходимо выполнить следующее действие: один разделить на четыре.
Получается, что степень 4-1 мы вычислили. Она равна рациональному числу 1/4. Для того чтобы вычислить другие значения, проводим следующие вычисления.
Предыдущее за числом 1/4 должно быть в два раза меньше. Чтобы его получить разделим 1/4 на 2.
Отсюда следует, что 1/4>1/16 в четыре раза.
Выполняя деление на четыре определим значения других степеней с целыми отрицательными показателями:
Расчеты приведены в таблицу 3.
Таблицы 3. Расчет степени с целыми отрицательными значениями степеней.
| Значение степени | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
Проанализировав значения в таблице 3, можно сделать следующий вывод: результаты степени с отрицательными значениями, прямо пропорциональны значениям с положительным результатом.
Данные вычисления и сравнения сведем в таблицу 4.
Таблица 4. Сравнение и анализ итоговых данных.
| -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Решим еще несколько примеров для закрепления материала.
Воспользуемся, уже изученным правилом вычисления значения степеней, у которых значение отрицательное.

Потому что, если z будет равен нулю, в знаменателе число выйдет равным ноль. По правилам математики на ноль делить нельзя.
1.Принцип вычисления тождественных преобразований
Все данные преобразования для натуральных и целых показателей одинаковы. Они, также, сохраняются и для степеней, которые имеют отрицательные значения.
Далее, при помощи примеров, закрепим полученные знания
Пример 1. Найти значение выражения 5−15 × 517
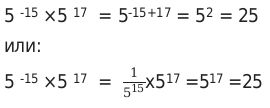
Вариант вычисления, первым способом, легче. Именно его чаще всего и применяют в процессе обучения.
Пример 2. Найти значение выражения (10−4)−1
Используем для расчета правило возведения в степень
(10−4)−1 = 10−4 × (−1) = 104 = 10000
Пример 3. Определить значение выражения (10−5)−1
Для этого применим правилом возведения степени в степень:
(10−5)−1 = 10−5 × (−1) = 105 = 10000
2.Перемещение степени между знаменателем и числителем
В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный.
При этом само значение выражения не поменяется.
Данный метод иногда используется при упрощении выражений.
Рассмотрим основные примеры:
Пример 1.
\[\frac{4^{2}}{4^{2}}=1\] — это выражение является верным, так как после преобразования степеней мы получаем 40. А как гласят правила алгебры — любое число в нулевой степени равно единице.
Пример 2. Перемещение значения степени из знаменателя дробного выражения \[\frac{1}{z^{2} x}\] в числитель \[\frac{1}{z^{2} x}=z^{-2} \times z^{-1}\]
Пример 3. Записать произведение 3x*(x + y)−4 в виде дроби, которая не имеет степени с отрицательным значением.
Выражение имеет множители 3 и (x + y)−4. Множитель 3 не изменяем, а множители (x + y)−4 заменяем на соответственно равную ему дробь \[\frac{1}{(x+y)^{4}}\]
Затем перемножим множитель 3 с числителем дроби \[\frac{1}{(x+y)^{4}}\]. В результате образуется дробь \[\frac{3}{(x+y)^{4}}\].
Итоговый результат: \[3(x+y)-4=3 x \frac{1}{(x+y)^{4}}=\frac{3}{(x+y)^{4}}\].
3.Возведение числа 10 в целую отрицательную степень
Вычисление степени для числа 10 происходит таким же образом, как и остальные числа.
На примерах рассмотрим более подробно.
Пример 1:
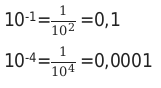
Если обратить внимание на пример, то мы увидим, что количество нулей в ответе равно показателю самой степени.
В случае, если значение степени равно -3, то в ответе количество нулей получается равным трем.
Проще говоря, чтобы возвести 10 в отрицательную степень, можно только записать количество необходимых нулей перед единицей. Но, не забыть поставить запятую, перед вторым нулем.
Пример 1:
10 -2=0,01;
Пример 2:
10 -3=0,001;
Пример 3:
10 -4=0,0001;
Пример 4:
10 -6=0,000001;
Пример 5:
10 -8=0,00000001.
4.Преобразование значений 0,1, 0,01, 0,001, где основанием степени является число 10
Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:
- указать отрицательный показатель степени;
- записать основание равным десяти.
Пример 1: Значение 0,01, где основание — число 10.
В числе 0,01 имеется два 0. Значит, оно будет представлено как 10 -2. Значение показателя равно значению нулей в числе 0,01.
0,01 = 10-2
Число 0,01 это значение деления 1/100, или 1/102
Пример 2: Значение 0,00001 в виде степени с основанием 10.
0,00001 = 10-5
5. Вид числа (значения) стандартный
Запишем число 4 000 в следующем виде 4 и 1 000
4 × 1 000
Значение 1 000 записать в виде значения 103. И тогда выражение будет иметь вид, как 4 × 103.
Именно такое выражение и называют стандартным видом. Он позволяет записывать большие и маленькие числа в более компактном виде.
Пример 1.
1,5× 1 000 = 1,5× 103
Пример 2.
0,158× 10 000 = 0,158× 104
Пример 3.
26× 1 000 000 = 26× 106
Стандартный вид числа имеет следующее выражение: z × 10m, где 1 ≤ z < 10 и m — целое число. Где:
z — исходное числовое значение, которое должно соответствовать неравенству 1 ≤ z < 10.
Возьмем для примера число 14. Подставив его в неравенство и проверим условие. 1 ≤ 14 < 10. Мы видим, что неравенство не соответствует условию. Поэтому приводим число 14 к виду, что бы неравенство соответствовало условию.
Для этого передвинем в числе 14 запятую влево на одну цифру и получим 1,4. Теперь неравенство удовлетворяет условию.
1 ≤ 1,4 < 10
Теперь наша задача состоит в том, чтобы записать произведение z × 10m. С числом z — у нас будет 1,4. Осталось правильно подобрать степень.
Число 14, после переноса запятой, свое значение утратило. Чтобы восстановить изначальное значение числа запятую нужно передвинуть обратно в правую сторону на одну цифру, то есть умножить число 1,4 на 10.
Значит, чтобы записать число 14 в стандартном виде, нужно представить его в виде произведения.
14 = 1,4 × 10¹

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Свойство степени с рациональным показателем
От целых показателей степени числа z мы переходим к рациональным показателем степеням. Далее мы определим степень с рациональным показателем, причем будем производить расчеты так, чтобы сохранялись все свойства степени с целым показателем. Это обязательно, потому что целые числа являются непосредственно частью рациональных чисел.
Свойство степени с рациональным показателем значительно облегчает изучение степеней в целом. Изучив данный метод, можно легко научится решать задачи различного уровня сложности.
Рассмотрим основные свойства степени с рациональным показателем.
а) Произведение степеней с основаниями, которые имеют одинаковые значения.

б) Свойство частного значения.
Доказательство данного свойства идентично по сравнению с предыдущим.
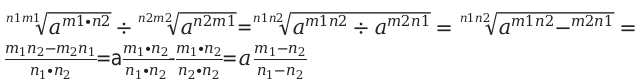
в) Свойство произведения в степень в виде дроби
г) Свойство степени в степени.

д) Свойство сравнения степеней со значениями равными между собой
zm<ym — условие любых положительных значений z и y, z < y и любом рациональном значении m>0.
Отсюда следует неравенство: m<0·zm>ym
е) Условие рациональных чисел
zx<zy, при следующем условии:
x > y при 0<z<1; если z>0 zx>zy
Для того чтобы доказать все перечисленные условия, нам необходимо будет вспомнить, понятие степени с дробным показателем.
Рассмотрим свойство с рациональным показателем на примере:
Пример №1.
Пример № 2: необходимо вычислить \[8 \frac{2}{3}=\frac{1}{8^{\frac{2}{3}}}=\frac{1}{8\left(\frac{1}{3}\right)}=\frac{1}{2^{2}}=\frac{1}{4}\]
Преобразуя уравнение, мы получим следующий вид: 415=(43)5далее записываем в виде \[\sqrt[5]{\left(4^{3}\right)^{5}}=4^{3}=64\]
Степень с иррациональным и действительным показателем
Понятно, что множество действительных чисел можно рассматривать как объединение множеств рациональных и иррациональных числовых значений. Поэтому степень с действительным показателем принято считать определенным значением, когда определяются степень с рациональным показателем и степень с иррациональным показателем. Про степень с рациональным показателем было подробно рассмотрено в предыдущем пункте, осталось лишь разобраться подробнее со степенью с иррациональным показателем.
Иррациональное число — это число, которое, в первую очередь не может быть представлено в виде обыкновенной дроби, а только в виде бесконечной дроби.
Основные свойства иррациональных чисел:
— сумма из двух положительных иррациональных чисел может равняться рациональным числом.
— множество иррациональных чисел встречаются повсюду на протяжении всей числовой прямой
— между двумя любыми различными рациональными числами имеется иррациональное число.
Свойства иррациональных степеней, как было уже сказано ранее, включают в себя все предыдущие характеристики с других свойств степеней
1. a p ⋅ a q = a p + q;
2. a p : a q = a p – q;
3; ( a ⋅ b ) p = a p ⋅ b p;
4.( a : b ) p = a p : b p;
5. ( a p ) q = a p ⋅ q;
6. a p < a q ap =0 a>0, то a p > aq ap>aq;
7. a p < a q ap =0 a>0, то a p > aq ap>aq.
Таким образом, все степени, показатели которых pp и qq являются действительными числами, при условии
a > 0 a>0 обладают теми же свойствами.
Для определения степени с иррациональным показателем, часто конечный результат определяют с точностью до определенного знака.
Для того, чтобы вычислить число в иррациональной степени, нужно его число возвести в дробную степень.
zzn
Более точный результат мы получим, при наиболее приближенном значении.
Рассмотрим на примере: \[3^{\sqrt{3}}\]
Решение:
— Вычислим значение корня из 3.
— Определим приближенное значение до четырех цифр после запятой.
— Возведем значение три в степень и получим значение, в виде бесконечной дроби:
— Далее необходимо округлить полученное числовое значение до четырех знаков.
Иррациональный процесс расчета, метод очень трудоемкий. В основном все вычисления в алгебре строятся таким методом, чтобы избавиться от иррациональности. Он несет в себе неудобства расчета, ведь иррациональность не дает возможность получить точность определения окончательного значения.















