Как найти площадь треугольника, формулы треугольника
Понятие площади
Площадью (S) геометрической фигуры именуется численная величина, характеризующая её размер.
В этом собственно и состоит понятие площади. У неё есть следующие два свойства:
- Площадь равных геометрических фигур имеет одно и то же числовое значение;
- Величина площади фигуры равняется сумме единичных площадей квадратов, на которые её можно разделить.
Пример 1.
Пусть у нас имеется прямоугольник в котором укладывается 7 клеток по вертикали и 12 по горизонтали. Это значит он будет иметь стороны a=7 и b=12.
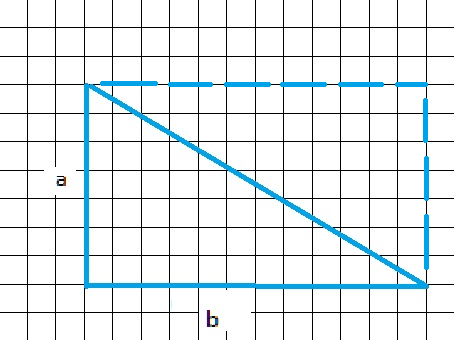
Из рисунка видно, что S нашего треугольника это половина таковой у прямоугольника. Последняя вычисляется так \[\mathrm{S}_{\text {прям }}=\mathrm{a} * \mathrm{~b}\]. Чтобы узнать площадь треугольника, разделим \[\mathrm{S}_{\text {прям }}\] на 2, тогда получим:
\[S= (a*b)/2\].
Подставляем численные значения (7*12)/2 = 42.
Как найти площадь треугольника, если мы знаем его основание и высоту
Площадь любого треугольника численно равняется половине произведения длины основания на высоту фигуры.
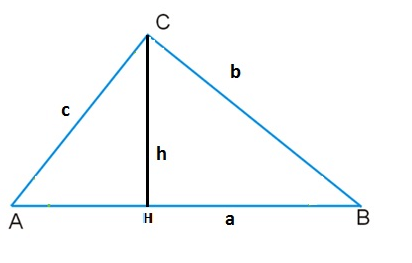
В нашем случае основанием считается сторона AB. Формула для S получается следующей:
\[S=(1/2)*AB*h \].
Доказательство:
Посмотрите рисунок. Из него ясно видно, что высота h делит ABC на 2 прямоугольных треугольника ACH и HCB.
По формуле (1) вычисление S каждого из них идёт так.
S(ACH) = (1/2)(AH)*h
S(HCB)=(1/2)(HB)*h
Чтобы вычислить площадь треугольника abc, нужно S(ACH) и S(HCB) сложить.
S=(1/2)(AH)*h+ (1/2)(HB)*h
Выносим (1/2) и h за скобки и получаем
(1/2)*h*(AH+HB)
Но AH+HB=AB, т. е.
S = (1/2)*AB*h, что и требовалось доказать.
Как видите, формулу площади треугольника получить и доказать достаточно легко.
Теперь о том, как найти площадь треугольника прибегнув к формуле Герона. Эта задача тоже не особо трудная.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Формула Герона для треугольника
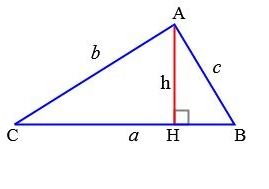
По формуле Герона S треугольника, имеющего стороны a, b, c равна:
P — полупериметр. Он равен
Доказательство:
Положим, что x=CH. В этом случае BH=a-x
С помощью теоремы Пифагора по отношению к AHC и AHB будем иметь
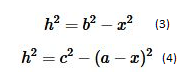
Из них следует, что
\[b^{2}-x^{2}=c^{2}-(a-x)^{2}\]
Отсюда легко найти
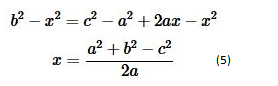
Чтобы найти h подставляем (5) в (3) и получаем
\[h=\sqrt{b^{2}-x^{2}}=\sqrt{b^{2}-\left(\frac{a^{2}+b^{2}-c^{2}}{2 a}\right)^{2}}\] (6)
Тогда S будет равняться
\[S=\frac{1}{2} \cdot a \cdot h=\frac{1}{2} \cdot a \cdot \sqrt{b^{2}-\left(\frac{a^{2}+b^{2}-c^{2}}{2 a}\right)^{2}}\] (7)
Преобразовав это выражение, получаем формулу Герона для площади треугольника.
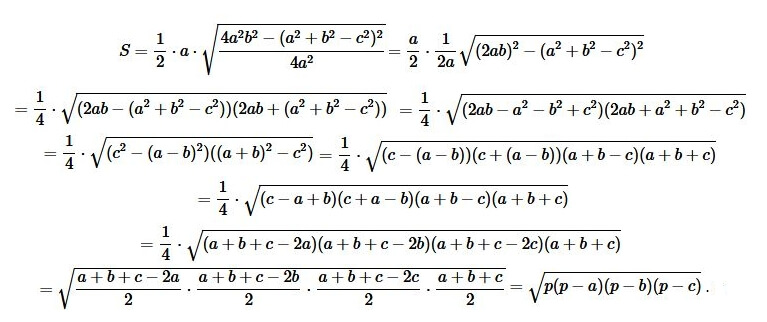
Вот так можно найти площадь треугольника по формуле Герона.
Площадь равностороннего треугольника
Площадь равностороннего треугольника можно вычислить по формуле:
\[S=\frac{\alpha^{2} \sqrt{3}}{4}\].
где a —длина одной из трёх сторон.
Для её доказательства употребим формулу Герона.
Полупериметр в нашем случае равен
p = (З/2)*a
Выражение под знаком корня в формуле Герона можно записать в виде
Выносим второй член произведения из-под корня и получаем
Далее так как p-a = (За-2а)/2=a/2 формула Герона для треугольника приобретает следующий вид
Выносим из-под корня a2 и 4 в знаменателе, в результате расчёта получаем
Что и требовалось доказать.















