Арксинус, арккосинус, арктангенс и арккотангенс числа
Данный тип функций решают задачу вычисления и определения угловых значений по известному заданному значению тригонометрической функции.
Например, синус какого угла будет иметь значение \[\frac{1}{2}\]
Напрашивается ответ, что это угол 60° или \[\frac{\pi}{3}\] , однако вспоминая о периоде значений косинуса, делаем вывод: углы, при которых косинус равен \[\frac{1}{2}\], существует достаточно много.
Данные тригонометрические функции являются обратными по значению. Они имеют множество характерных свойств:
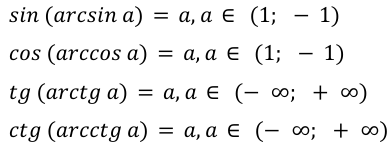
Проведем доказательство перечисленных свойств на примере значения арксинуса. Значение угла данной функции равняется числу a. И данное значение находится на промежутке чисел от -1 до +1.
sin(arcsin a)=a
Все остальные функции доказываются аналогично, согласно их определения.
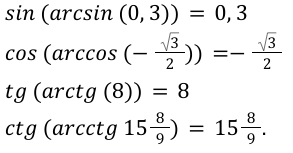
Определение значений обратных функций, будет иметь смысл при условии, что неизвестное число a будет делать в пределах от -1 до +1.
Противоположные значения для обратных значений функций арксинус, арккосинус, арктангенс, арккотангенс
Взаимосвязь функций противоположных чисел можно записать в следующем виде:

Перейдем к доказательству записанных выражений.
Доказательство арксинусов:
\[\text { Если }-1 \leq a \leq 1 \Rightarrow \arcsin (-a)=-\arcsin a .\]
Данная тригонометрическая функция имеет предел значений от \[-\frac{\pi}{2} \text { до } \frac{\pi}{2}\] и синус его равен -a.
Докажем, что — arcsin a находится в пределах \[-\frac{\pi}{2} до \frac{\pi}{2}\] и обоснуем, что sin (-arcsin a)=-a.
Для функции арксинус справедливо неравенство, следующего вида:\[-\frac{\pi}{2} \leq \arcsin a \leq \frac{\pi}{2}\].
Для того чтобы получить эквивалентное неравенство, нужно обе части равенства умножить на значение-1. После вычислений получим:\[-\frac{\pi}{2} \leq-\arcsin \mathrm{a} \leq \frac{\pi}{2}\].
Докажем, что sin ( − arcsin a ) = − a sin(-arcsin a)=-a.
Применим свойство противоположных углов и составим уравнение:
sin ( − a r c sin a ) = − sin ( a r c sin a )=-sin arcsin a.
Арккосинус доказывается следующим образом:
Записываем выражение: \[\arccos (-a)=\pi-\arccos a \text { при } a \in(-1,1)\]
Для этой функции принимает равенство \[0 \leq \arccos a \leq \pi\] обе части равенства нужно перемножить на значение равное -1 и изменить знаки на противоположные. Выполнив вычисления получим равенство: \[\pi \geq \pi-\arccos a \geq \pi\].
Чтобы доказать оставшиеся две функции, применяются аналогичные свойства и правила.
Правило противоположных чисел позволяет упростить процесс решения и исключает все операции при вычислении с отрицательными числами.
Например:
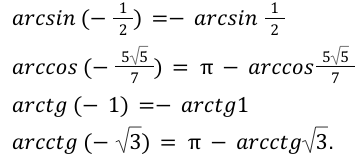
Принцип сложения обратных тригонометрических функций
Для тригонометрических функций, прямых или обратных, характерны простые математические свойства, а именно: сложение данных.
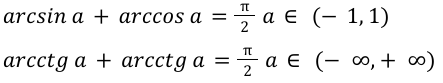
Составим доказательство функций для арксинуса и арккосинуса. Формулы arcsin и arccos в виде суммы, можно представить как \[\arcsin a=\frac{\pi}{2}-\arccos a\]. Затем применить определение, из которого следует, что арксинус — это число, которое относится пределу значений от \[-\frac{\pi}{2} \text { до } \frac{\pi}{2}\] , синус равняется a.
Обе части неравенства \[0 \leq \arccos a \leq \pi\] умножим на значение -1 и прибавим \[\frac{\pi}{2}\].
Выполнив все необходимые операции по вычислению заданного равенства, получим следующие выражения:
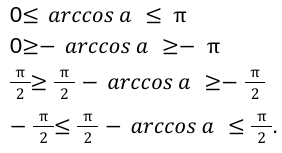
Для завершения доказательства запишем формулу: \[\sin \left(\frac{\pi}{2}-\arccos a\right)=\cos (\arccos a)=a\]
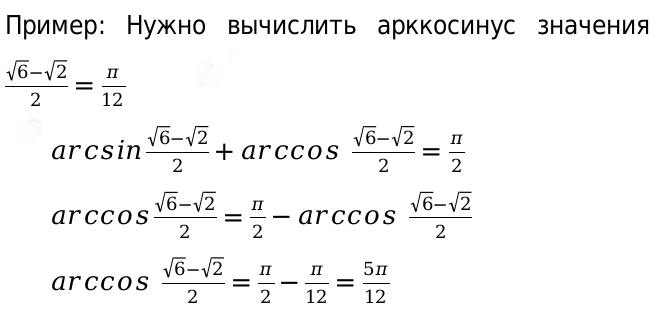
Сформулируем свойства рассматриваемых значений функций относительно синуса, косинуса, тангенса и котангенса.
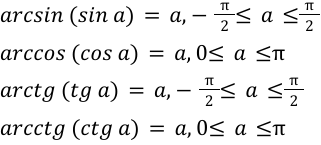
Значение arcsin (sin a) имеет смысл в том случае, если a относится к пределам \[-\frac{\pi}{2} ; \frac{\pi}{2}\] и выполняется условие \[-\frac{\pi}{2} \leq a \leq \frac{\pi}{2}\].
Аналогичные условия характерны и для других функций.
Пример: \[\arcsin \left(\sin \frac{8 \pi}{3}\right)=\frac{8 \pi}{3}\], является неверной, потому что \[\frac{8 \pi}{3}\], не удовлетворяет условию.
Главные значения: arcsin, arccos, arctg и arctg
Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \[0, \pm 30,45,60,90,120 \ldots \ldots \ldots \ldots \ldots \pm 180\] градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.
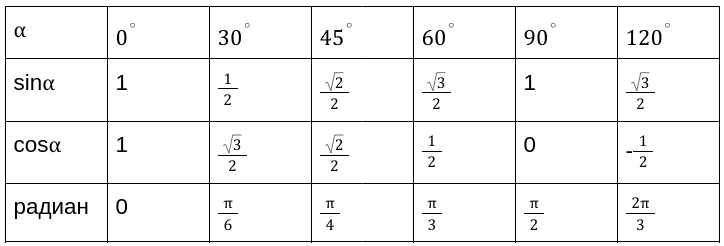
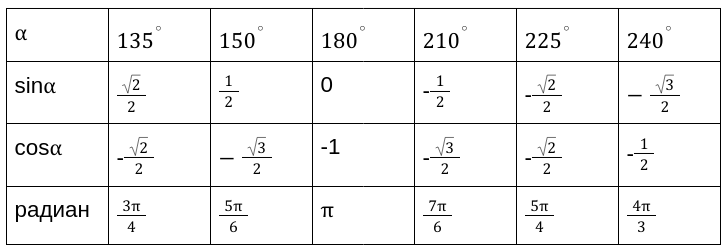
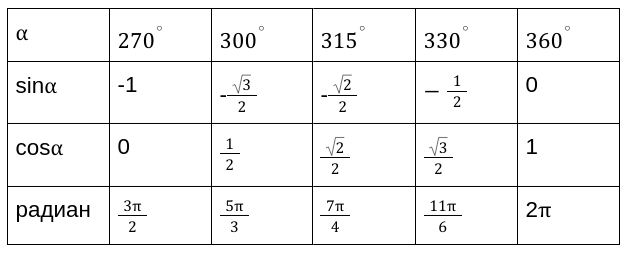
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.
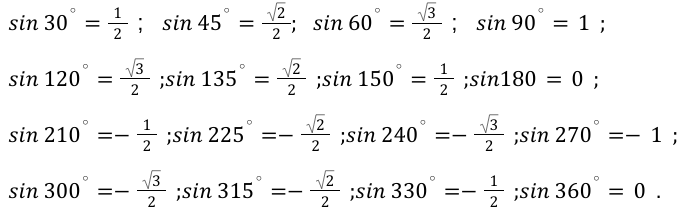
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.

Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.
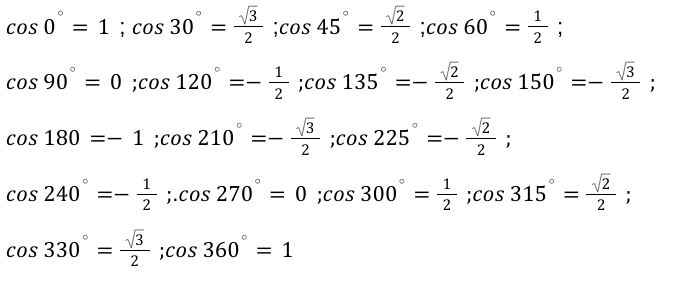
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.
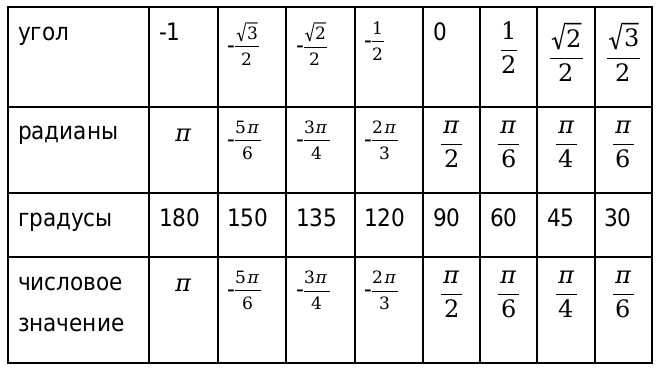
И напоследок остается вычислить значения арктангенса и арккотангенса.
Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:
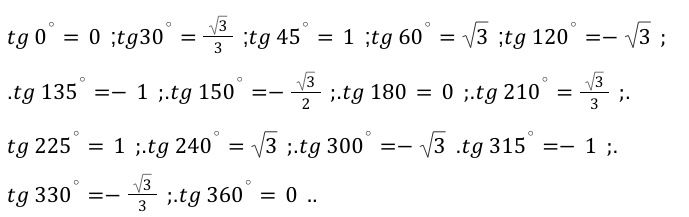
\[\operatorname{tg} 90^{\circ}, 270^{\circ}\] — данные угловые значения, не определяются, согласно основным законам геометрии и математики.
\[\operatorname{ctg} 0^{\circ}, 180^{\circ}, 360^{\circ}\]- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются
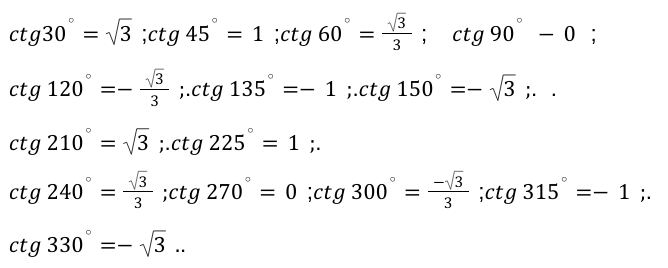
Далее все данные запишем в виде табличной формы.
Первая таблица для арктангенса
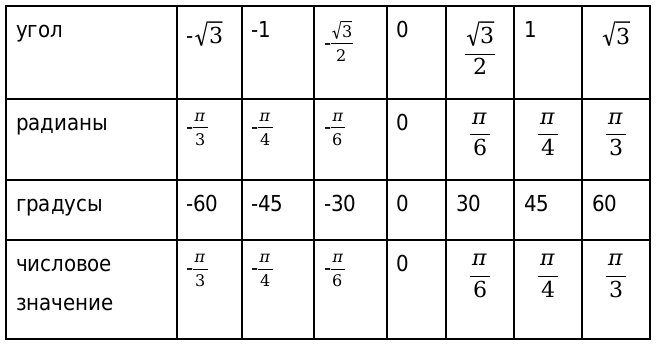
Вторая таблица для арккотангенса
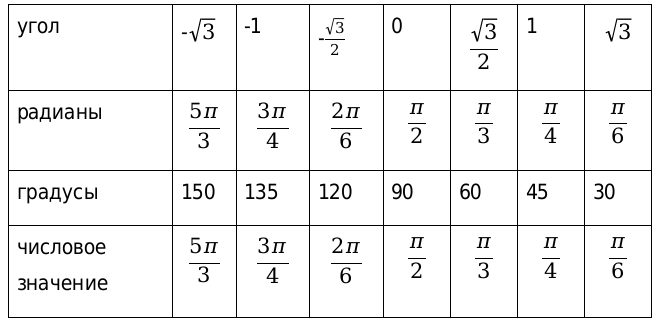
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
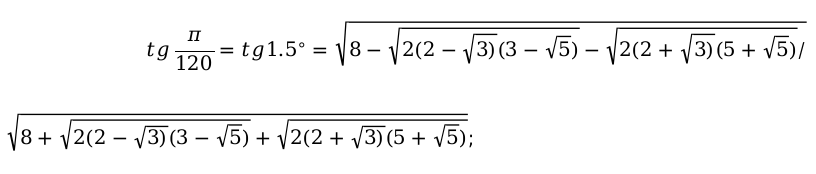
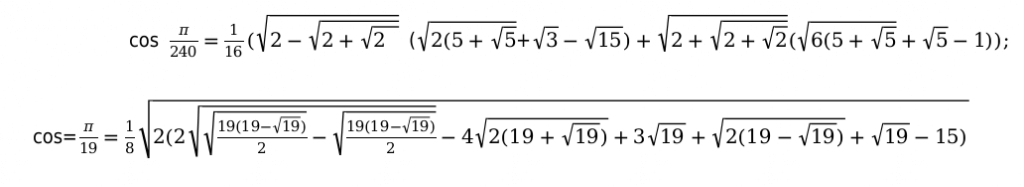
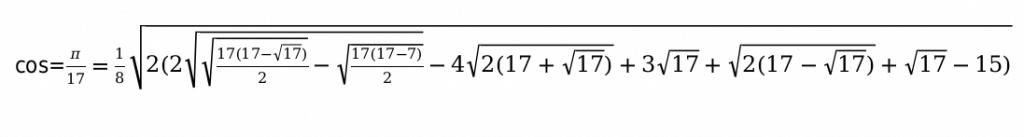
Основные способы, которые помогут заполнить таблицу функций тригонометрии.
Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec).
На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения.
Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.
В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.


Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:
Пример решения:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102
Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение. Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.

Арксинус (y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
| Свойства функции | Функции y=arcsin х |
| E(f) | \[-1 \leq x \leq-1\] |
| D(f) | \[-\frac{\pi}{2}<y<\frac{\pi}{2}\] |
| наличие четности | Нечётная, т.к. arcsin(-x)= — arcsin x |
| характер графика направление | возрастание |
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y).
| Свойства | Функции y=arccos х |
| E(f) | \[-1 \leq x \leq-1\] |
| D(f) | \[0 \leq y \leq \pi\] |
| Чётности | Данное свойство ей не характерно. Иными словами отсутствует. |
| Монотонность | Убывающая |
Арктангенс ( y = arctg x ) – характеризуется, как обратное значение функции относительно тангенса.
Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | \[\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\] | \[(0 ; \pi)\] |
| Характер функции | Нечётная | Нечётная |
| Периоды | Возрастающая | Убывающая |















