Формулы понижения степени в тригонометрии
Формулы понижения степени являются одним из видов основных тригонометрических формул. Они выражают степени (2, 3, …) тригонометрических функций синус, косинус, тангенс, котангенс через синус и косинус первой степени, но кратного угла (α, 3α, …α, 3α, … или 2α, 4α, …2α, 4α, …).
Запишем данные тождества для тригонометрических функций от 2-й по 4-ю степень угла αα, а также для угла α2α2 и для произведения синус на косинус. Для удобства разделим их на группы.
Для квадрата
Формулы данной группы, в частности две первые, наиболее используемые. Их используют при решении тригонометрических тождеств, интегралов и т. д.
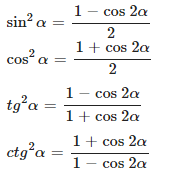
Для куба
Формулы этой группы и другие встречаются не так часто, но их также важно знать:
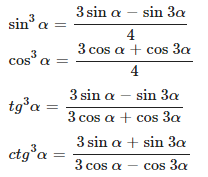
Для решения уравнений 4-й степени
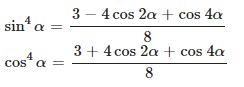

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Формулы половинного угла тригонометрических функций
Указанные ниже тождества — это формулы половинного угла. В случае, если они указаны в таком формате, их можно отнести и к тождествам понижения степени.
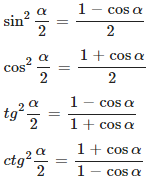
Произведение синус на косинус
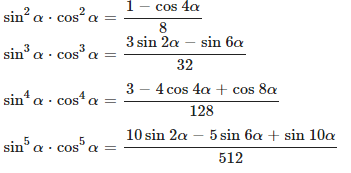
Доказательство
Сейчас обратимся непосредственно к решению формул понижения степени тригонометрических функций.

Формула понижения степени тангенса и котангенса автоматически выводится из определений этих функций. Например:
Если формулы тройного угла
Равность для синуса и косинуса можно доказать, если использовать 2 раза тождества понижения квадратов:
Общий вид формул понижения степени
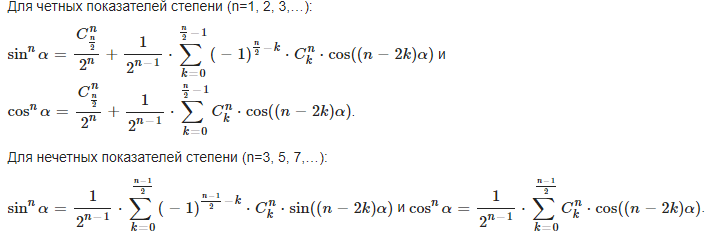
Многие не знают как решить задачу с применением формулы понижения степени, поэтому мы подготовили отличный пример:

Важно: формулы понижения степени в тригонометрии больше используют для решения тождеств и преобразовании выражений уравнений.















