Нахождение высоты трапеции
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
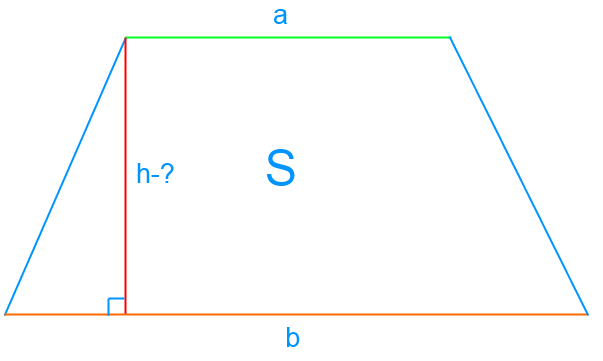
Чтобы вычислить площадь S трапеции мы используем формулу:
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
\[h=\frac{2 \times 50}{(4+6)}=10 \mathrm{~cm}\]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
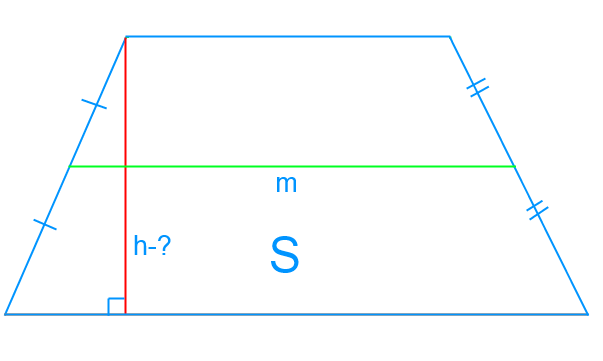
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
\[h=\frac{S}{m}\], будет ответом.
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
\[h=\frac{200}{20}=10 \mathrm{~cm}\]
Ответ: 10 см
Высота прямоугольной трапеции
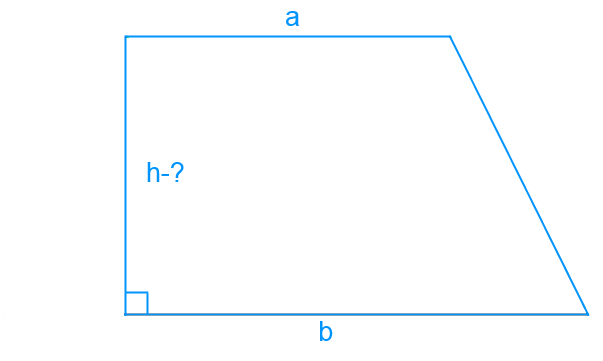
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
\[A C^{2}=A D^{2}+D C^{2}\] может быть записан
\[15^{2}=14^{2}+x^{2}\]
\[x=\sqrt{\left(15^{2}-14^{2}\right)}=\sqrt{(225-196)}=\sqrt{29} \mathrm{см}\]
Ответ: \[\sqrt{29} \mathrm{см}\], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нахождение высоты через стороны
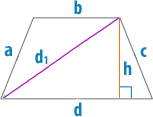
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
\[h=\sqrt{2^{2}-\left(\frac{(4,5-2,5)^{2}+2^{2}-2 \sqrt{2}^{2}}{2(4,5-2,5)}\right)^{2}}=\sqrt{4}=2 см\]
Ответ: h=2 см.
