Понятие единичной окружности и ее связь с тригонометрией
Единичная окружность и определение точки абсцисс
Единичная окружность — представлена окружностью с радиусом, который равняется единичному значению, и ее центр (ось) находится в начале системы координат, которая обозначается как прямоугольной декартовой.
Угол поворота для единичной окружности
Данное понятие тесно связано с разделом математики, а именно тригонометрией. Движение по окружности и можно представить, как угол поворота. Однако величина самого угла поворота, не является зависимой от радиуса самой окружности. Именно это свойство и создает простоту использования единичной окружности при всех процессах решения в математике.
Данную окружность можно задать следующим уравнением:
По вышеизложенному уравнению можно определить поворот конкретной заданной точки на единичной окружности.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Координаты точек единичной окружности
Применяя основные точки единичной окружности, можно сформулировать и вывести основные определения тригонометрических функций:
- косинус;
- синус;
- тангенс;
- котангенс.
Затем выделяют основные свойства и с их помощью составляются главные тождества.
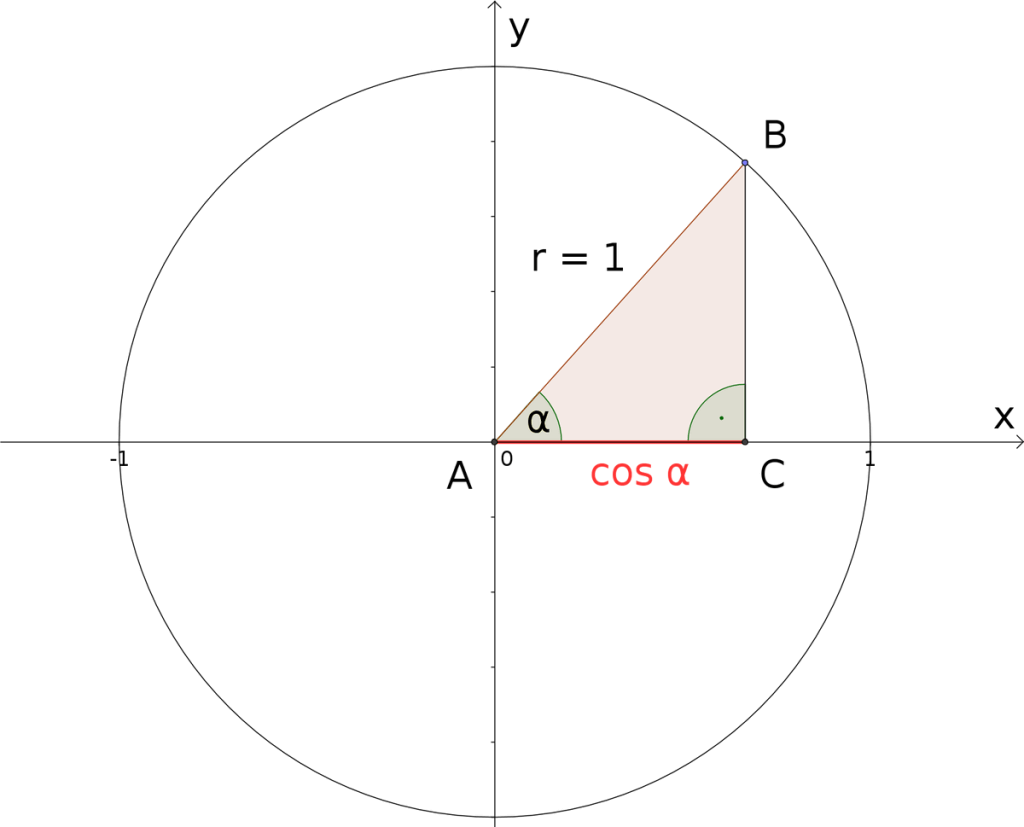
Основное тригонометрическое тождественное уравнение можно вывести при помощи главных функций и записать в следующем виде.
Выполнение любых работ по математике
Популярные статьи
Примеры решения матриц с ответами
Общее уравнение плоскости
Метод Крамера – теорема, примеры решений
Нахождение площади фигуры ограниченной линиями y=f(x), x=g(y)