Сумма и разность синусов и косинусов
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
В математике применяются основные определения, связанные с тригонометрией. А именно:
- синус — соотношение стороны противолежащего катета к стороне гипотенузы, (sin);
- косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos);
Стоит выделить главные тригонометрические тождества, существующие в математике:
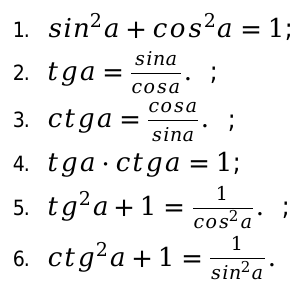
Применим основные формулы тригонометрии, решая задачи.
Пример:
Известно: \[\cos \alpha=0.8\];
Необходимо определить: косинус, тангенс, котангенс, соответствующего угла a.
Решение:
Для определения значения косинуса в квадрате, возводим число 0,8 в квадрат и вычисляем синус. Полученное значение подставляем в формулу и можем определить тангенс угла 0,8. Таким же методом, вычисляем котангенс
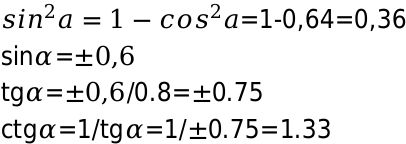
Решение довольно простое и особых сложней не вызывает.
Основные формулы для приведения заданных значений:
Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.
Существует два основных способа, использования формул приведения:
- Если угол можно записать как \[(\pi / 2 \pm \alpha)\] или \[\left(3^{*} \pi / 2 \pm \alpha\right)\], то название функции меняется с косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде \[(\pi \pm \alpha)\] или \[(2 * \pi \pm \alpha)\], то название функции не меняется.
- Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.
Используя основные определения математики, а именно тригонометрии. Можно определить нужные нам данные.
Значения функций тригонометрии на для основных угловых значений.
- синуса (sin):
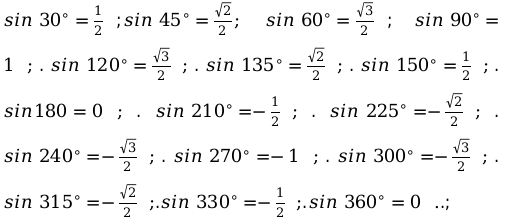
- косинуса (cos):
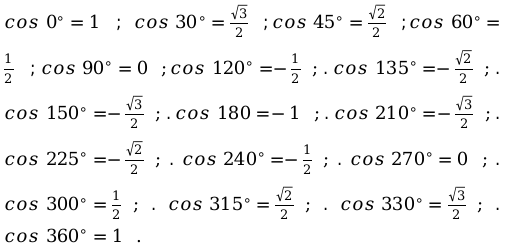
Преобразовав формулы сложения, мы получим тригонометрические уравнения угла.
Формулы кратности значения угла:
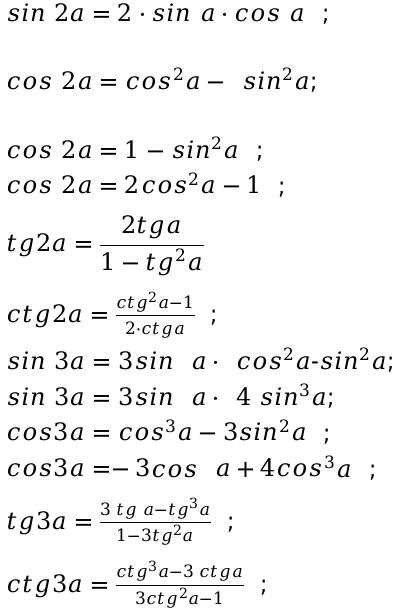
Формулы угла, определяющие половину значения (половинного угла):
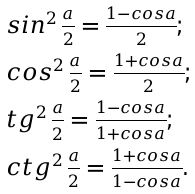
Более подробно в данном материале мы рассмотрим все уравнения суммы и разности, связанные именно с функцией косинус и синус.
Основные формулы для определения суммы и разности cos и sin
Перейдем к рассмотрению к простой форме разности и суммы функций.
Рассматриваемое уравнений можно представить, как — произведение. Преобразовать на множители косинус или синус, и тем самым упростить процесс вычисления.
Составим и запишем основные формулы для функции синус.
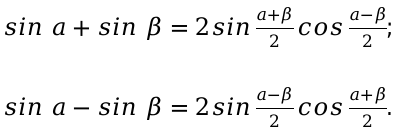
Следующим основным шагом, будет составить уравнения для косинуса. Применим все изученные свойства данной функции тригонометрии и вычислим правильный ответ.
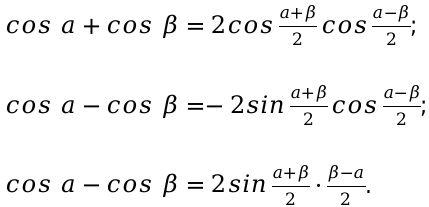
Выведем основные формулы для решения функций двух угловых значений. Для этого нужно применить составленные выше формулы сложения и вычитания. Их рассмотрение было в предыдущих материалах, посвященных тригонометрии. Поэтому лишний раз не стоит их заново переписывать. Так как рекомендовалась их обязательно заучить наизусть. Для более быстрого и правильного решения уравнений. И для последующего использования при изучении других смежных тем, где эти функции применяются.
Формулы можно представить также в виде полусуммы и полуразности угловых значений и получить следующие формулы.
Запишем уравнение для каждого угла раздельно и получим следующие формулы в виде уравнения:
Сравним записанные формулы для угловых значений. Проанализировав их становится очевидно, что полученные суммы функций одинаковы по значению.
Выведем основную формулу для решения:
Далее первую часть выражения преобразуем, для этого применим формулу для сложения функций. Значения, которые находятся после знака равно, преобразуются при помощи формулы синуса для разности.
Подставляя в формулу значения, получаем следующее выражение:
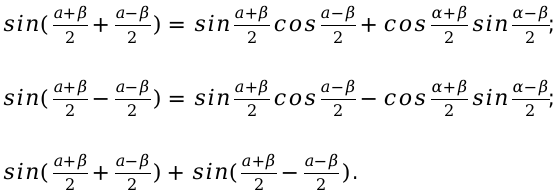
Далее необходимо раскрыть скобки и полученные значения привести в подобные слагаемые. Произведя все действия мы в конечном итоге получаем нужную нам формулу.
Запишем формулу следующего вида:
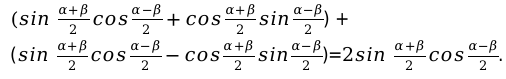
Другие, формулы преобразуются аналогичным способом

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Итоговые формулы сложения и вычитания тригонометрических функций
Формула определения разности для синуса:
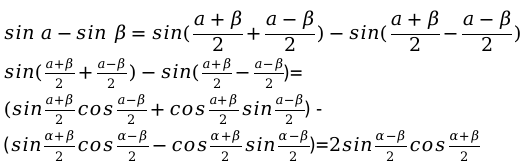
Формула для расчета суммы косинуса:
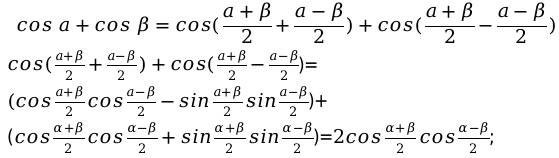
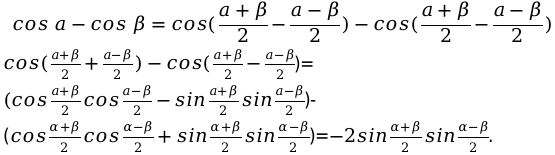
Рассмотрим на практике применение изученного материала. Для этого решим несколько задач, подставляя числовые угловые значения
Пример №1:
По заданию нужно проверить сумму угловых значений для изученной функции подставив данные в формулу.
Заданы значения: \[\alpha=\frac{\pi}{2} ; \beta=\frac{\pi}{6}\].
Подберем нужную формулу и произведем вычисление:
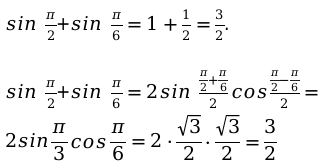
Пример №2:
В этом примере рассмотрим вариант решения и применения формулы, для разности функции синуса.
Заданы следующие значения.
Углы: \[\alpha=165^{\circ}, \beta=75^{\circ}\]
Подставим угловые значения в формулу:
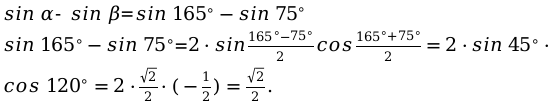
Пример №3:
Нужно найти сумму тригонометрической функции.
Для этого заданы угловые значения.
Применяя основные изученные формулы, решим данную задачу.
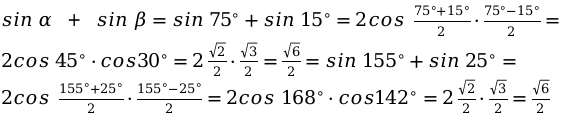
Применяя вышеизложенные формулы можно перейти к произведению функций.
В целом, данная тема, считается основой в алгебре. Однако стоит вспомнить, что данные функции имеют главную роль и в других технических науках.
Они встречаются во многих теоремах, особенно это свойственно для физики.
Для всех технических наук, характерна взаимосвязь между основными законами и теоремами. Поэтому для успешного решения задач разного уровня, необходимо изучать и уметь их всех применять на практике.















